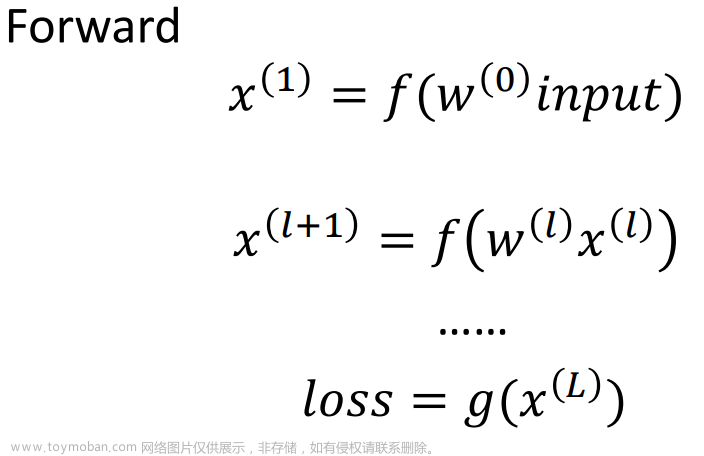一、计算图
计算图,是一种用来描述计算的有向无环图。
我们假设一个计算过程,其中
X
1
\mathbf{X_1}
X1、
W
1
\mathbf{W_1}
W1、
W
2
\mathbf{W_2}
W2、
Y
\mathbf{Y}
Y都是
N
N
N维向量。
X
2
=
W
1
X
1
\mathbf{X_2} = \mathbf{W_1}\mathbf{X_1}
X2=W1X1
y
=
W
2
X
2
\mathbf{y} = \mathbf{W_2}\mathbf{X_2}
y=W2X2
L
=
∑
i
=
1
N
(
Y
i
−
y
i
)
2
L = \sum_{i=1}^N(Y_i - y_i)^2
L=∑i=1N(Yi−yi)2
上述过程,用计算图表现出来,就是下图。

从这张图中可以看出, X 1 \mathbf{X_1} X1、 W 1 \mathbf{W_1} W1、 W 2 \mathbf{W_2} W2、 Y \mathbf{Y} Y是直接创建的,它们是叶子节点, X 2 \mathbf{X_2} X2、 y \mathbf{y} y、 L L L是经过计算得到的,它们不是叶子节点。
计算导数。
如果我们想跨越若干层计算导数,如计算
∂
L
∂
X
1
\frac{\partial L}{\partial \mathbf{X_1}}
∂X1∂L的值,则需要根据求导的链式法则,一层一层的计算下去。
∂
L
∂
X
1
=
∂
L
∂
y
∂
y
∂
X
2
∂
X
2
∂
X
1
\frac{\partial L}{\partial \mathbf{X_1}}=\frac{\partial L}{\partial \mathbf{y}}\frac{\partial \mathbf{y}}{\partial \mathbf{X_2}}\frac{\partial \mathbf{X_2}}{\partial \mathbf{X_1}}
∂X1∂L=∂y∂L∂X2∂y∂X1∂X2
∂
L
∂
W
1
=
∂
L
∂
y
∂
y
∂
X
2
∂
X
2
∂
W
1
\frac{\partial L}{\partial \mathbf{W_1}}=\frac{\partial L}{\partial \mathbf{y}}\frac{\partial \mathbf{y}}{\partial \mathbf{X_2}}\frac{\partial \mathbf{X_2}}{\partial \mathbf{W_1}}
∂W1∂L=∂y∂L∂X2∂y∂W1∂X2
∂
L
∂
W
2
=
∂
L
∂
y
∂
y
∂
W
2
\frac{\partial L}{\partial \mathbf{W_2}}=\frac{\partial L}{\partial \mathbf{y}}\frac{\partial \mathbf{y}}{\partial \mathbf{W_2}}
∂W2∂L=∂y∂L∂W2∂y
二、backward()函数
PyTorch提供了autograd包来自动根据输入和前向传播构建计算图,其中,backward函数可以很轻松的计算出梯度。
Tensor在pytorch中用来表示张量,上例中的 X 1 \mathbf{X_1} X1、 W 1 \mathbf{W_1} W1、 W 2 \mathbf{W_2} W2都是张量,且均为直接被我们创建的。如果我们想使用autograd包让它们参与梯度计算,则需要在创建它们的时候,将.requires_grad属性指定为true。
注意,在pytorch中,只有浮点类型的数才有梯度,因此在定义张量时一定要将类型指定为float型。
x1 = torch.tensor([2, 3, 4, 5], dtype=torch.float, requires_grad=True)
print(x1)
输出为
当然对于没有指定.requires_grad属性的向量,也可以在后续进行指定,或者使用requires_grad_函数进行指定。
w1 = torch.ones(4)
w1.requires_grad = True
print(w1)
w2 = torch.Tensor([1, 2, 3, 4])
w2.requires_grad_(True)
print(w2)
输出为
接下来进行运算操作。
x2 = x1 * w1
print(x2)
输出为
在这个运算中,pytorch会构建一个动态地创建一个计算图,即动态计算图(Dynamic Computation Graph, DCG),计算图中的每一个节点,都会封装若干个属性。下图为
X
2
=
X
1
W
1
\mathbf{X_2} = \mathbf{X_1}\mathbf{W_1}
X2=X1W1这一计算的计算图。
解释一下各属性的含义。
- data:存储的Tensor的值。
- requires_grad:该节点是否参与反向传播图的计算,如果为True,则参与计算;如果为False则不参与。
- grad:存储梯度值。requires_grad为False时,该属性为None;requires_grad为True且在调用过其他节点的backward后,grad保存对这个节点的梯度值,否则为None。
- grad_fn:表示用于计算梯度的函数,即创建该Tensor的Function。如果该Tensor不是通过计算得到的,则grad_fn为None;如果是通过计算得到的,则返回该运算相关的对象。
举个例子,a为直接创建的Tensor,b和c由计算得到,则a、b、c的grad_fn如下所示。
a = torch.ones(2, 2, requires_grad=True)
print(a.grad_fn)
b = a + 2
print(b.grad_fn)
c = b * b * 3
print(c.grad_fn)
输出为
- is_leaf:用True和False表示是否为叶子节点。
然后继续计算直到得到 L L L。这个过程是正向传播的过程,会继续动态的生成计算图。
y = x2 * w2
Y = torch.ones(2, 2, requires_grad=True)
L = (Y - y).mean()
在本例中,如果我们想求 ∂ L ∂ X 1 \frac{\partial \mathbf{L}}{\partial \mathbf{X_1}} ∂X1∂L,则需要首先使用backward()函数对 L L L做反向传播。backward()实际上是通过DCG图从根张量追溯到每一个叶子节点,然后计算将计算出的梯度存入每个叶子节点的.grad属性中。由于 L L L是一个标量,因此backward()函数中不需要传入任何参数。代码如下
L.backward()
这一步后 L L L针对每一个变量的梯度都会被求出,并存放在对应节点的.grad属性中。如果我们想要 ∂ L ∂ X 1 \frac{\partial L}{\partial X_1} ∂X1∂L,只需要读取x1.grad即可。
print(x1.grad)
三、backward()函数的参数grad_tensor
上面的例子中,作为输出的 L L L是一个标量,即神经网络只有一个输出,backward不需要传入参数。但如果输出是一个向量,计算梯度需要传入参数。例如
x = torch.tensor([0.0, 2.0, 8.0], requires_grad=True)
y = torch.tensor([5.0, 1.0, 7.0], requires_grad=True)
z = x * y
print(z)
结果如下。可以看出z也是一个张量。
如果想求z对x或y的梯度,则需要将一个外部梯度传递给z.backward()函数。这个额外被传入的张量就是grad_tensor。
z.backward(torch.FloatTensor([1.0, 1.0, 1.0]))
为什么要传入这个张量呢?传入这个参数,本质上是将向量对向量求梯度,通过加权求和的方式,转换成标量对向量求梯度。在数学上,向量对向量求导的结果是雅可比矩阵(Jacobian Matrix)。

如果我们再引入与向量 y \mathbf{y} y同型的向量 v {\mathbf{v}} v,标量损失用 l l l表示,则令
v = [ ∂ l ∂ y 1 . . . ∂ l ∂ y m ] = ∂ l ∂ y {\mathbf{v}}= \left[ \frac{\partial l}{\partial y_1} \quad ... \quad \frac{\partial l}{\partial y_m} \right] = \frac{\partial l}{\partial {\mathbf{y}}} v=[∂y1∂l...∂ym∂l]=∂y∂l
这样反过来
l
=
y
v
T
=
∑
i
=
1
m
v
i
y
i
l = \mathbf{y} \mathbf{v}^\text{T}=\sum_{i=1}^mv_iy_i
l=yvT=∑i=1mviyi
所以说
l
l
l是向量
y
\mathbf{y}
y的加权和。
向backward()函数中传入的grad_tensor实际上就是向量 v {\mathbf{v}} v,求的梯度实际上就是
∂
l
∂
x
=
∂
l
∂
y
∂
y
∂
x
=
v
J
{\frac{\partial l}{\partial {\mathbf{x}}}} =\frac{\partial l}{\partial {\mathbf{y}}} \frac{\partial {\mathbf{y}}}{\partial {\mathbf{x}}}=\mathbf{v}\mathbf{J}
∂x∂l=∂y∂l∂x∂y=vJ
从线性代数的角度上解释,也可以理解为
∂
l
∂
x
\frac{\partial l}{\partial {\mathbf{x}}}
∂x∂l就是
∂
y
∂
x
{\frac{\partial {\mathbf{y}}}{\partial {\mathbf{x}}}}
∂x∂y在向量
v
{\mathbf{v}}
v上的投影。参考
backward不传入参数时,默认为传入backward(torch.tensor(1.0))。文章来源:https://www.toymoban.com/news/detail-407335.html
另外,.grad属性在反向传播过程中是累加的,每一次反向传播梯度都会累加之前的梯度。因此每次重新计算梯度前都要将梯度清零。文章来源地址https://www.toymoban.com/news/detail-407335.html
x.grad.data.zero_()
到了这里,关于PyTorch:梯度计算之反向传播函数backward()的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!