(蓝桥杯第十一届决赛)试题D：本质上升序列（动态规划）-Toy模板网

这篇具有很好参考价值的文章主要介绍了(蓝桥杯第十一届决赛)试题D：本质上升序列（动态规划）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

(蓝桥杯第十一届决赛)试题D：本质上升序列（动态规划）

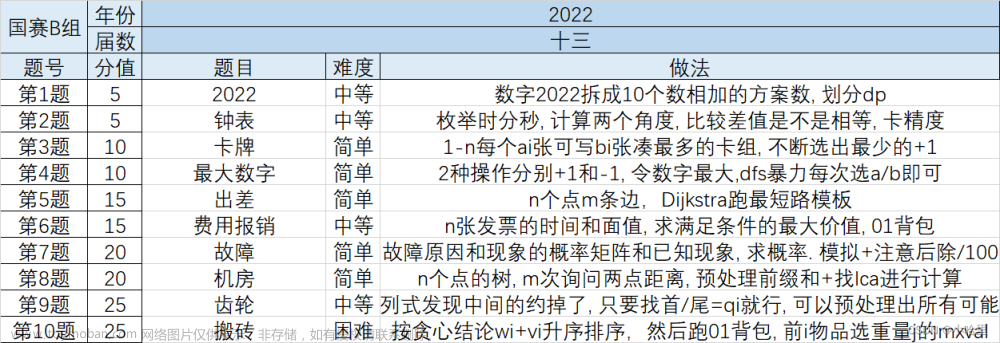
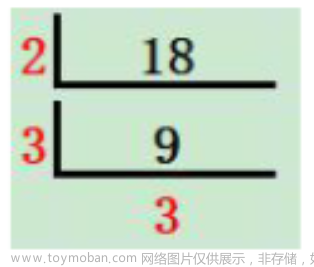
先把题目中的字符串给出来：tocyjkdzcieoiodfpbgcncsrjbhmugdnojjddhllnofawllbhfiadgdcdjstemphmnjihecoapdjjrprrqnhgccevdarufmliqijgihhfgdcmxvicfauachlifhafpdccfseflcdgjncadfclvfmadvrnaaahahndsikzssoywakgnfjjaihtniptwoulxbaeqkqhfwl

分析：虽然这只是一道填空题，但是我觉得这个还是有一定的思考意义的，所以我今天就把他当作一个正常的大题来分析：

设f[i]表示以i结尾的本质不同的递增子序列，在这里我们先分析一个字符串bab，很显然f[1]=1,f[2]=1,f[1]=1是因为只有b，f[2]=1是因为只有a，那么f[3]=？，如果说是1那么就是只有ab，如果说是2那么就是含有ab和b两个递增子序列，但是很显然b在之前已经被计算过了，所以我们在这里如果使得f[3]=2的话就会重复计算，因为如果前面和后面字母重合的话我们只需要考虑一次，所以在这里我把他归结为前面字母的贡献，也就是说上面所分析的字符串中f[3]=1,也就是只包含ab这一种情况。如果我们能够求出来所有的f[i]，由f数组的定义我们可以知道，只要最后把所有的f数组求个和即可得到答案。

下面我们来进行动态转移方程的推导：

现在拿abcsca来举例

f[1]=1(a)

f[2]=2(b, (f[1]后面接上b)ab)

f[3]=4(c, (f[1]后面接上c)ac, (f[2]后面接c)bc,abc)

f[4]=8(s, (f[1]后面接上s)as, (f[2]后面接s)bs,abs (f[3]后面接上s)cs,acs,bcs,abcs)

f[5]=0（无）

f[6]=0（无）

发现当遇到第二个c时，第二个c的贡献就变成了0，换句话说关于c的贡献都在前一个c中，因为如果只考虑第一个c及其出现位置之前的字符的话，以第二个c为结尾的贡献和以第一个c结尾的贡献是相同的，第一个c出现的位置是3，那么第二个c与上一个c出现前面的字符形成的递增子序列是重复的，这些都在前一个c中已经被计算过了，所以当前的c的贡献就应该从上一次出现c的位置的后一位开始考虑，如果某个字符字典序小于c且出现在上一个c的后面，在以这个字符结尾的所有本质不同的递增子序列后面加一个c就可以构成一个新的递增子序列，这应该属于当前c的贡献，如果这个字符大于等于c就不予考虑，按照这个方法我们就可以求得所有的f数组，这样我们就可以得到最终的答案了。注意我们这样进行更新的话只能对某个字母第一次出现的位置初始化为1，第二次出现就不能初始化为1了，因为在之前已经被计算过了。

下面是这种思路的代码：

#include<cstdio>
#include<iostream>
#include<cstring>
#include<vector>
#include<algorithm>
#include<map>
#include<cmath>
#include<queue>
using namespace std;
const int N=303;
long long f[N];//f[i]代表以i结尾的本质不同的序列数 
int last[30];//last[i]代表字符i最后一次出现的位置 
int main()
{
	string s;
	cin>>s;
	long long len=s.size();
	s=" "+s;//让下标从1开始
	for(int i=1;i<=len;i++)
	{
		if(!last[s[i]-'a'+1])//如果这个字符没有出现过，则单个字符的贡献应该属于这个字符，反之由于已经被计算过则不能再初始化为1 
			f[i]=1;//初始化为1（只包含自身）
		for(int j=last[s[i]-'a'+1]+1;j<i;j++)//从上次出现这个字母的后一个位置开始更新f[i] 
			if(s[i]>s[j]) f[i]+=f[j];
		last[s[i]-'a'+1]=i;//记录该字母最后一次出现的位置
	}
	long long ans=0;
	for(int i=1;i<=len;i++)
		ans+=f[i];
	cout<<ans;
	return 0;
}

当然我们也可以直接从前往后进行考虑，比如考虑更新f[i]，我们就遍历1~i-1，假如s[j]<s[i],那我们就直接加上f[j]，相当于我们直接在以第j个字符结尾的合法序列结尾加一个字符s[i]，这样也是一个合法序列,若s[i]==s[j]，我们就减去f[j],因为我们在利用f[1~j-1]进行更新f[i]时就相当于利用f[j]来更新f[i]，因为最后一个字母为s[i]的代价已经被计算进f[j]中，所以要减去这部分，其实这样思考的本质和上面那样是相同的，就是看大家怎么考虑了，由于我们是采用先加上重合的部分最后减去重合的部分，所以我们就不需要像上面那样查询当前字母上一次出现的位置，那么这样我们一开始f[i]就应该初始化为1,代表每一个字母的贡献（只包含这一个字母本身）。

下面是这种方法的代码：

#include<cstdio>
#include<iostream>
#include<cstring>
#include<vector>
#include<algorithm>
#include<map>
#include<cmath>
#include<queue>
using namespace std;
const int N=303;
long long f[N];//f[i]代表以i结尾的本质不同的序列数 
int main()
{
	string s;
	cin>>s;
	long long len=s.size();
	s=" "+s;//让下标从1开始 
	for(int i=1;i<=len;i++) 
	{
		f[i]=1;//初始化为1（只包含自身）
		for(int j=1;j<i;j++)
		{
			if(s[i]==s[j])//减去重复计算的部分
				f[i]-=f[j];
			else if(s[i]>s[j])
				f[i]+=f[j];
		}
	}
	long long ans=0;
	for(int i=1;i<=len;i++)
		ans+=f[i];
	cout<<ans;
	return 0;
}

最后大家直接把我一开始给定的那个字符串作为输入代入方程即可得到答案：3616159文章来源地址https://www.toymoban.com/news/detail-407759.html

到了这里，关于(蓝桥杯第十一届决赛)试题D：本质上升序列（动态规划）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！