LeetCode：二叉树的前、中、后序遍历——如何创建一棵【二叉树】-Toy模板网

这篇具有很好参考价值的文章主要介绍了LeetCode：二叉树的前、中、后序遍历——如何创建一棵【二叉树】。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

🍎道阻且长，行则将至。🍓

🌻算法，不如说它是一种思考方式🍀

算法专栏： 👉🏻123

一、🌻二叉树

1.简介

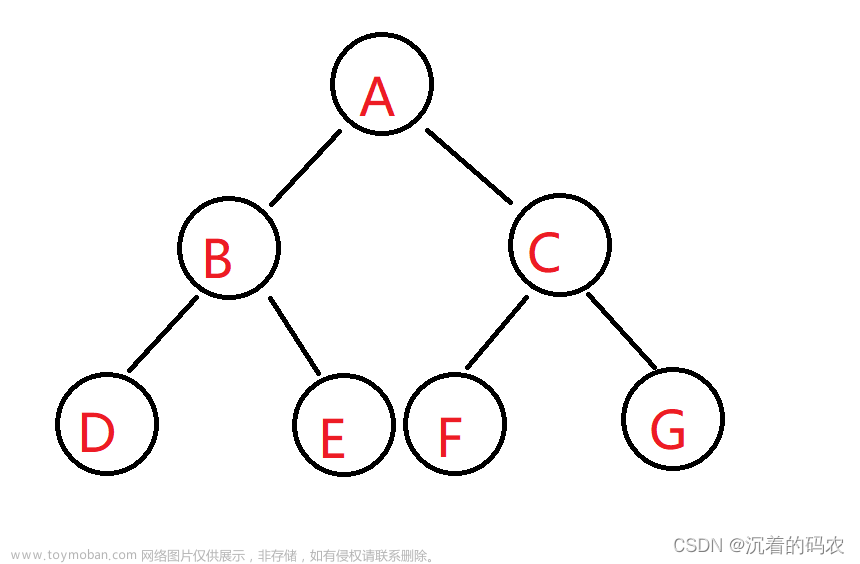
二叉树是一种树形数据结构，其每个节点最多只有两个子节点。通常将节点分为三种类型：根节点、内部节点和叶子节点。其中，根节点是二叉树的唯一访问起点，内部节点具有一个父节点和两个子节点，而叶子节点没有子节点。二叉树的底层数据结构可以使用链表或数组来实现。

二叉树的应用非常广泛，例如在计算机科学中，二叉树是许多数据结构的基础，例如二叉搜索树、红黑树、B树等。在计算机图形学中，二叉树可以用于表示场景图和计算机三维图形学中的视锥体。二叉树在编程面试中也是一个热门话题，它与许多基本数据结构和算法有着紧密的联系。

二叉树的操作包括插入、删除、查找、遍历等。其中，遍历是二叉树最基本的操作之一，包括前序遍历、中序遍历、后序遍历和层次遍历等。二叉树的复杂度取决于树的高度，平衡二叉树和自平衡二叉树用于减少树高和提高性能。

2.种类

二叉树可以分为以下几种种类：

满二叉树：每个节点都有两个子节点，并且所有叶子节点都在同一层上。
完全二叉树：除了最后一层，其他层的节点数都达到了最大值，并且最后一层的节点从左到右依次排列。
平衡二叉树：左右子树的高度之差不超过 1。
二叉搜索树（BST）：左子树上所有节点的值均小于它的根节点的值，右子树上所有节点的值均大于它的根节点的值，并且左右子树也分别为二叉搜索树。
红黑树：一种自平衡的二叉搜索树，它满足以下条件：每个节点不是红色就是黑色；根节点是黑色的；每个叶子节点（NIL节点）都是黑色的；任何相邻的节点不能同时为红色；从任一节点到其子树中每个叶子节点的路径都包含相同数量的黑色节点。
B树：一种多路平衡查找树，可以支持高效的查找、插入和删除操作。B树节点上可以存储多个关键字，同时每个节点都具有多个子节点，通常用于磁盘等外存储器上。
AVL树：一种自平衡的二叉搜索树，它的任何节点的左右子树的高度最多相差1。当一次插入或删除操作导致树不再满足平衡性时，需要通过旋转节点来进行调整，使树重新满足平衡性。

3.构造与遍历

二叉树的构造

以下图的二叉树为例子，假设给出数组格式：要求来构造一棵二叉树：
LeetCode：二叉树的前、中、后序遍历——如何创建一棵【二叉树】

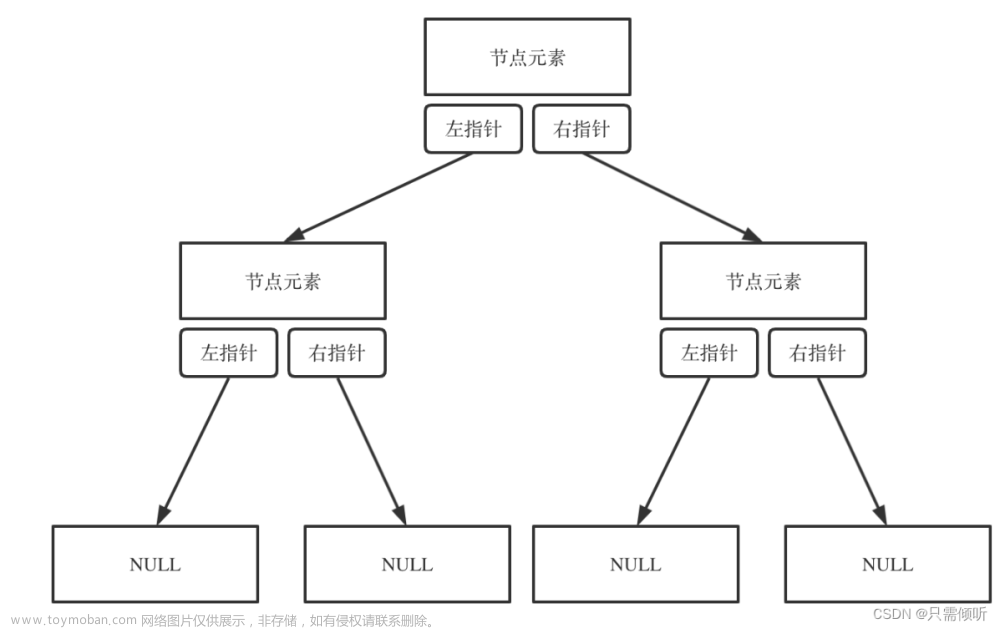
二叉树的体：定义一个二叉树类添加节点值，左右叶子，并提供构造方法和set方法

class TreeNode1 {
    int val;
    TreeNode1 left;
    TreeNode1 right;

    TreeNode1() {
    }
    TreeNode1(int val) {
        this.val = val;
    }
    TreeNode1(int val, TreeNode1 left, TreeNode1 right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }

    public void setVal(int val) {
        this.val = val;
    }
    public void setLeft(TreeNode1 left) {
        this.left = left;
    }
    public void setRight(TreeNode1 right) {
        this.right = right;
    }
}

创建子节点方法
对于节点和数组下标有一种对应关系：左子树节点下标是i*2+1，右子树节点下标是i*2+2

public static void creatNode(TreeNode1 p, char[] root1, int i) {
    if (i >= root1.length)
        return;
    p.setVal(root1[i]);//父节点

    if (i*2+1 < root1.length ) {
        //左子树  *2+1
        if (root1[i * 2 + 1] != ' ') {
            p.left = new TreeNode1();
            creatNode(p.left, root1, i * 2 + 1);
        } else p.left = null;
    }

    if (i*2+2 < root1.length ) {
        //右子树  *2+2
        if (root1[i * 2 + 2] != ' ') {
            p.right = new TreeNode1();
            creatNode(p.right, root1, i * 2 + 2);
        } else p.right = null;
    }
}

main函数在中根据数组内容创建头结点，使用creatNode进行子节点构造

    public static void main(String[] args) {
        char[] root1 = {5, 4, 6, 1, 2, 7, 8};
        TreeNode1 root = new TreeNode1();
        creatNode(root, root1, 0);

        List list = Solution144.preorderTraversal(root);
        for (Object o : list) {
            System.out.print(o);
        }
    }

二叉树的遍历

二叉树的遍历方法包括前序遍历、中序遍历、后序遍历和层次遍历：

前序遍历：先访问根节点，然后访问左子树，最后访问右子树。也可以描述为“根 - 左 - 右”的访问顺序。
LeetCode：二叉树的前、中、后序遍历——如何创建一棵【二叉树】

中序遍历：先访问左子树，然后访问根节点，最后访问右子树。也可以描述为“左 - 根 - 右”的访问顺序。
LeetCode：二叉树的前、中、后序遍历——如何创建一棵【二叉树】

后序遍历：先访问左子树，然后访问右子树，最后访问根节点。也可以描述为“左 - 右 - 根”的访问顺序。

层次遍历：从上到下，从左往右依次访问每个节点。

其中，前序、中序和后序遍历都是深度优先遍历（DFS），而层次遍历是广度优先遍历（BFS）。遍历方法的选择取决于具体应用场景。例如，前序遍历可以用来复制整棵树，中序遍历可以用来对二叉搜索树进行排序，后序遍历可以用来释放内存等。层次遍历则可以用来按层遍历树，或者求树的宽度等。

二、🍀LeetCode：二叉树的前、中、后序遍历

🌱144、先序遍历
🌱94、中序遍历
🌱144、后序遍历

题目描述：给你二叉树的根节点 root ，返回它节点值的前序、中序、后序遍历。
来源：力扣（LeetCode）
难度：简单

🌴解题

1.先序遍历

这三种遍历使用递归方法只需要修改添加节点元素时机就可以了。

class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> list=new ArrayList<>();
        visitTree(root,list);
        return list;
    }

    private static void visitTree(TreeNode root, List<Integer> list) {
        if(root==null)
            return;
        list.add(root.val);
        //left
        if(root.left!=null)
            visitTree(root.left,list);
        //right
        if(root.right!=null)
            visitTree(root.right,list);
    }
}

LeetCode：二叉树的前、中、后序遍历——如何创建一棵【二叉树】

2.中序遍历

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {        
        List<Integer> list=new ArrayList<>();
        visitTree(root,list);
        return list;
    }

    private static void visitTree(TreeNode root, List<Integer> list) {
        if(root==null)
            return;        
        //left
        if(root.left!=null)
            visitTree(root.left,list);
        list.add(root.val);
        //right
        if(root.right!=null)
            visitTree(root.right,list);
    }
}

LeetCode：二叉树的前、中、后序遍历——如何创建一棵【二叉树】

3.后序遍历

class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> list=new ArrayList<>();
        visitTree(root,list);
        return list;
    }
    private static void visitTree(TreeNode root, List<Integer> list) {
        if(root==null)
            return;        
        //left
        if(root.left!=null)
            visitTree(root.left,list);       
        //right
        if(root.right!=null)
            visitTree(root.right,list);
            list.add(root.val);
    }
}