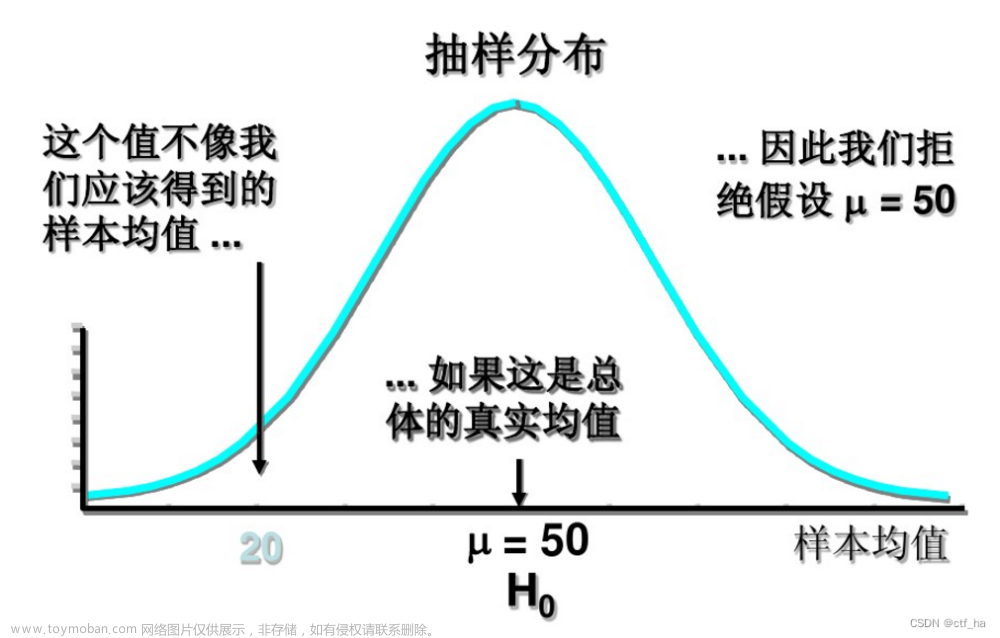
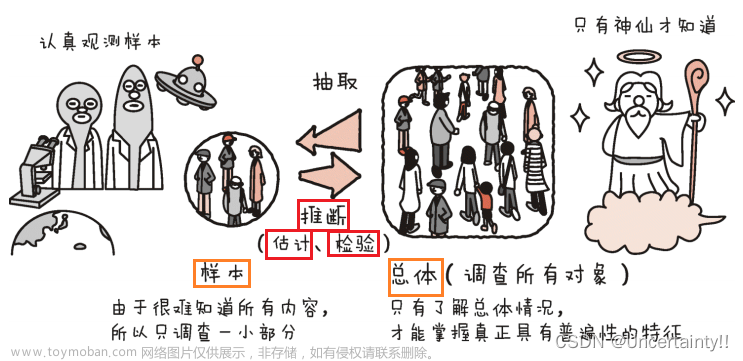
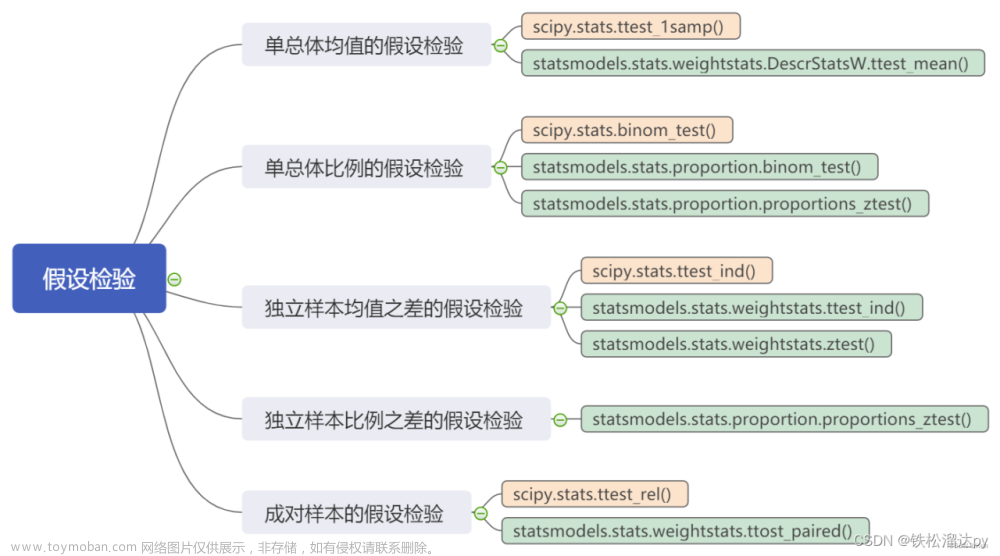
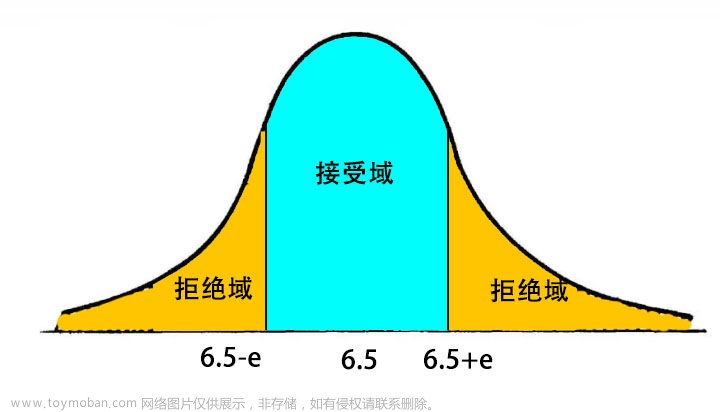
单总体参数的假设检验

单总体均值的检验
DescrStatsW.ztest_mean()
| statsmodels.stats.weightstats.DescrStatsW.ztest_mean(value=0, alternative='two-sided') | |
| 参数 |
说明 |
| value |
假设的均值 |
| alternative |
备择假设的形式,可选值:‘two-sided’, ‘larger’, ‘smaller’ |
weightstats.ztest()
| statsmodels.stats.weightstats.ztest(x1, x2=None, value=0, alternative='two-sided') | |
| 参数 |
说明 |
| x1, x2 |
独立样本数据,x2可为None,用于单总体检验 |
| value |
假设值 |
| alternative |
备择假设的形式,可选值:‘two-sided’, ‘larger’, ‘smaller’ |
例1: 国家要求含水量不超过4%,能否认为该生产厂商该批次的饼干符合要求?(显著水平取0.05)
单侧检验




返回值均为一个元组,第一个元素是计算出的统计量,第二个元素是p值
p=0.67 远大于 0.05,因此没有理由拒绝原假设,即没有理由认为该厂商生产的该批次饼干是不合格的。
DescrStatsW.ttest_mean()
| statsmodels.stats.weightstats.DescrStatsW.ttest_mean(value=0, alternative='two-sided') | |
| 参数 |
说明 |
| value |
假设的均值 |
| alternative |
备择假设的形式,可选值:‘two-sided’, ‘larger’, ‘smaller’ |
ttest_1samp()
| scipy.stats.ttest_1samp(a, popmean) | |
| 参数 |
说明 |
| a |
样本数据 |
| popmean |
假设均值 |
例2: 某移动通信公司对其用户进行满意度评估,公司认为用户满意度应该超过82分,为此公司进行了小规模的调查,得到25各用户评价满意度得分。试在显著性水平0.05条件下,对该公司的用户满意度进行评估。
单侧检验


p值远大于0.05, 没有充分理由拒绝原假设,即没有理由认为该公司的用户总体评价会大于82分。


注意:re是双侧检验的p值,如果备择假设取“<”符号:当t>=0时,进行判定得单侧p值=1-Pvalue/2; t<0时,p=Pvalue/2; 取“>”符号:当t>=0时,p=Pvalue/2; t<0时,p=1-Pvalue/2
单总体比例的假设检验
binom_test() 二项分布检验
| scipy.stats.binom_test(x, n=None, p=0.5, alternative=’two-sided’) | |
| 参数 |
说明 |
| x |
‘成功’的样本数量 |
| n |
样本总数量 |
| p |
假设的比例值 |
| alternative |
备择假设的形式,可选值:‘two-sided’, ‘greater’, ‘less’ |
proportions_ztest() 正态分布检验
| statsmodels.stats.proportion.proportions_ztest(count, nobs, value=None, alternative='two-sided') | |
| 参数 |
说明 |
| count |
‘成功’的样本数量 |
| nobs |
样本总数量 |
| value |
假设的比例值 |
| alternative |
备择假设的形式,可选值:‘two-sided’, ‘larger’, ‘smaller’ |
*smaller: prop < value; larger: prop > value
例3: 一批产品中随机抽取100个,95个合格,5个不合格,根据相关规定,该种产品合格率应当大于97%,那么在显著性水平a=0.05下,能否认为该批次产品不合格?


p值明显大于0.05,故不能拒绝原假设,可以认为该批次产品合格
两总体参数的假设检验

两个独立样本均值之差的假设检验
ttest_ind() t检验
- scipy.stats库
| scipy.stats.ttest_ind(a, b, axis=0, equal_var=True) | |
| 参数 |
说明 |
| a, b |
两组样本数据,应具有相同的形状(shape) |
| axis |
多维数组的数据读取方向 |
| equal_var |
是否要求方差齐性 |
- statsmodels模块
| statsmodels.stats.weightstats.ttest_ind(x1, x2, alternative='two-sided', usevar='pooled', value=0) | |
| 参数 |
说明 |
| x1, x2 |
两组样本数据,应具有相同的形状(shape) |
| alternative |
备择假设的形式,可选值:‘two-sided’, ‘larger’, ‘smaller’ |
| usevar |
是否要求方差齐性: pooled – 要求,unequal – 不要求 |
| value |
指定原假设取等号时的检验值 |
例4: 为了检验两种新生产工艺对电池续航能力是否有明显的影响,随机抽取了两种新工艺生产的同批次电池,在同一型号笔记本电脑上的放电时间(小时)。设显著性a=0.01,检验这两种工艺对电池续航时间影响是否有显著差异。

battery.csv
按照工艺分类,提取为两个DataFrame


68为自由度:70-2

大样本也可以采用z检验
独立样本比例之差的假设检验
两个总体比例是否有差异或检验其差异的具体数值; 通常用Z统计量进行检验
proportions_ztest() 正态分布检验
与单总体检验几乎相同,If this is array_like,注意nobs和count长度相同
关于 value:In the case of a two-sample test, the null hypothesis is that prop[0] - prop[1] = value, where prop is the proportion in the two samples. If not provided value = 0 and the null is prop[0] = prop[1]. 即,双总体检验时,value是两个比例之差,若没有给出value则默认为0。
在两个样本检验中,smaller意味着备择假设成立,而larger意味着 ,即:
| smaller | |
| larger |
例5: 某出版集团为了对旗下两本时尚杂志进行精确的市场定位,分别对两本杂志读者的性别进行了随机的抽样调查,试在显著性水平g=0.01条件下分析两本杂志读者性别的差异性。
假设经过经验判断,订阅了杂志1的女性占比为0.4,订阅了杂志2的女性占比为0.7,检验二者的差异是否超过了0.3。


统计性别为Female的读者对两本杂志的选择情况

统计所有读者对两本杂志的选择情况

p值远大于0.05, 没有充分理由拒绝原假设,二者的差异没有超过0.3,故两本杂志读者的性别没有显著差异
成对样本的假设检验
两个样本不互相独立,但是组成成对样本的不同个体之间的观测值是相对独立的,因此,可以先把两个样本中配对的观测值逐个相减,形成一个由独立观测值组成的样本,然后用单样本检验方法取进行统计推断
ttest_rel()
| scipy.stats.ttest_rel(a, b, axis=0) | |
| 参数 |
说明 |
| a, b |
两组样本数据,应具有相同的形状(shape) |
| axis |
多维数组的数据读取方向 |
例6: 为考察某市市民生活的幸福程度,连续多年对固定样本进行调查。随着社会经济的快速发展,幸福度是否会得到提升呢?(设显著性水平a=0.05) 随机抽取了2015,2016两年中200个样本进行分析。
假设幸福度没有得到提升


p远大于0.05,无法拒绝原假设,不能认为市民的幸福度得到显著提升。
或者:假设幸福度得到了提升,,

说明样本均值中看,第二年比第一年的幸福度高,但p值远远大于0.05,不能拒绝原假设,故可以认为幸福度得到了提升。这样与第一种假设得出的结论完全相反,这是因为原假设只能被证伪,而不能被证实!想证实的结论应该设置为备择假设而不是原假设!故给出一些原假设与备择假设选取时尽量遵循的规则:
双侧检验
问: 有无显著变化
验证: 没有显著变化
原假设: 有显著变化,等号放在原假设
单侧检验
问:有无显著提高
验证:有显著提高
原假设:没有显著提高,等号放在原假设文章来源:https://www.toymoban.com/news/detail-408135.html
 文章来源地址https://www.toymoban.com/news/detail-408135.html
文章来源地址https://www.toymoban.com/news/detail-408135.html
到了这里,关于python统计(二)假设检验的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!