非参数检验——Wilcoxon 检验 & Friedman 检验与 Nemenyi 后续检验-Toy模板网

这篇具有很好参考价值的文章主要介绍了非参数检验——Wilcoxon 检验 & Friedman 检验与 Nemenyi 后续检验。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

最近看论文，看到了Wilcoxon signed-rank test（符号秩检验），咱也不知道是个啥，就学习了一下，这里做一下笔记，方便以后查阅。

非参数检验

概念

数据描述的三个角度：集中趋势，离散程度和分布形态。

常用统计推断检验方法分为两大类：参数检验和非参数检验。

参数检验通常是假设总体服从正态分布，样本统计量服从T分布的基础之上，对总体分布中一些未知的参数，例如总体均值、总体方差和总体标准差等进行统计推断。

如果总体的分布情况未知，同时样本容量又小，无法运用中心极限定理实施参数检验，推断总体的集中趋势和离散程度的参数情况。这时，可以用非参数检验，非参数检验对总体分布不做假设，直接从样本的分析入手推断总体的分布。

非参数检验和参数检验的对比

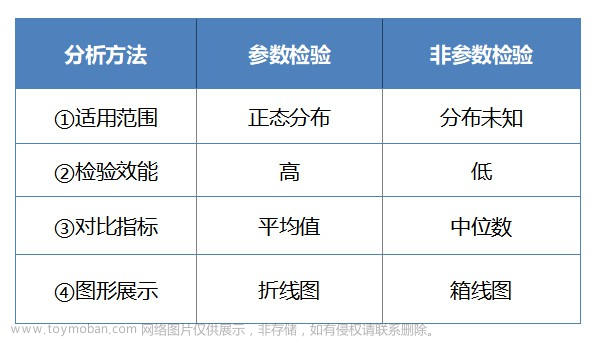
非参数检验——Wilcoxon 检验 & Friedman 检验与 Nemenyi 后续检验
① 适用范围：

非参数检验用作参数检验的替代方法，当数据不满足正态性时，将使用非参数检验。因此，关键是要弄清楚是否具有正态分布。如果数据大致呈现"钟型"分布，则可以使用参数检验。

② 检验效能：

如果数据满足参数分布，应该优先选择参数检验方法。愿因在于参数检验的检验效能要高于非参数检验。尤其是在样本数较大的情况下，参数检验结果较为稳健，所以即使不服从正态分布，也会选择参数检验。

③ 对比指标：

参数检验一般用平均值反映数据的集中趋势；但由于数据不满足正态分布，在非参数检验中如果再使用平均值描述显然不太准确（比如常被吐槽的人均收入），此时中位数是更好的选择。

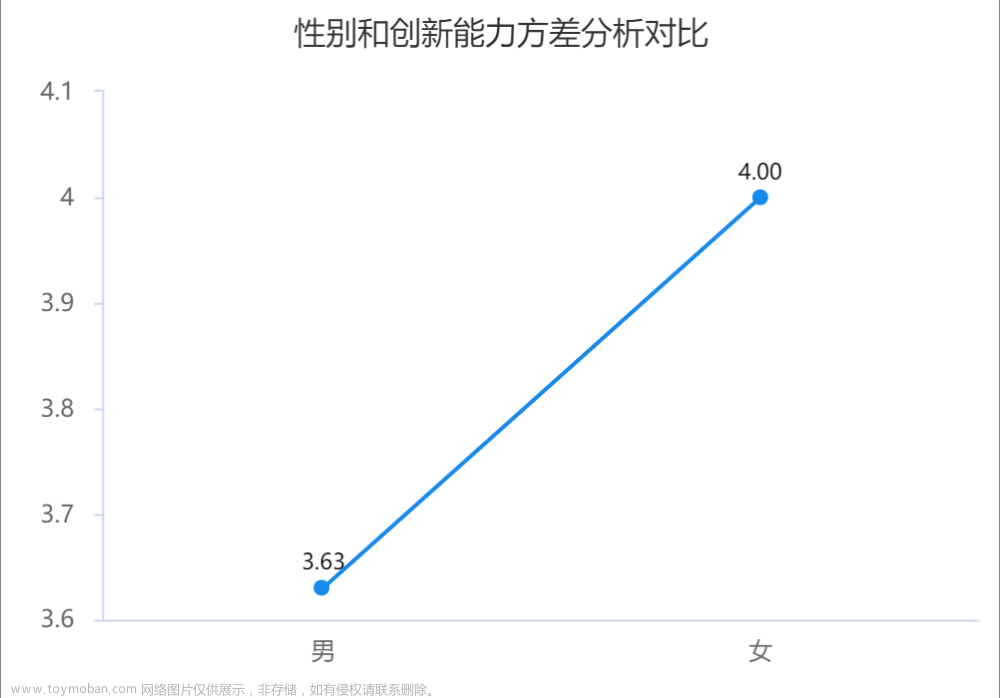
参数检验分析结果

参数检验用平均值及标准差描述数据分布请况。
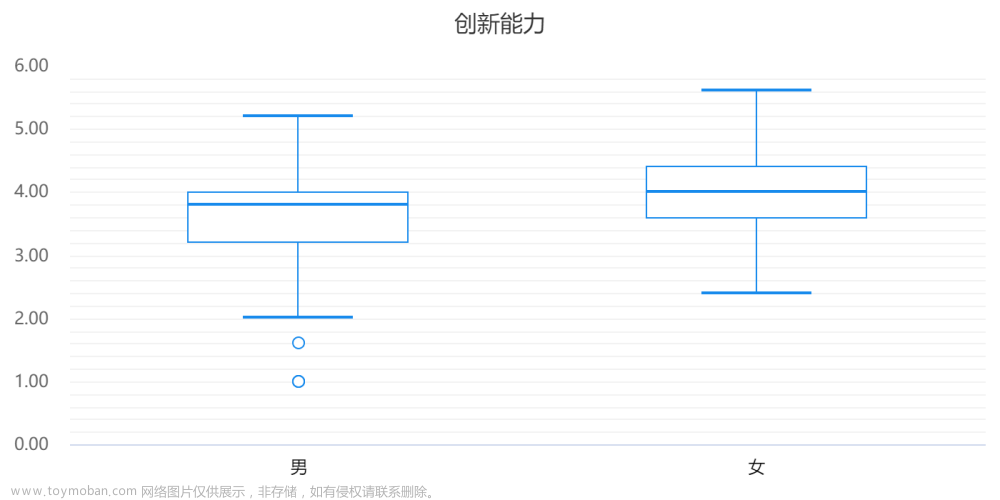
非参数检验分析结果

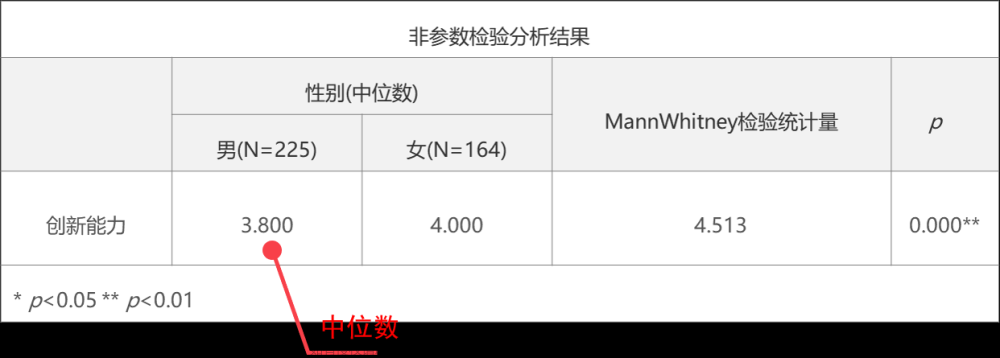
非参数检验结果中使用的是中位数描述差异。

④ 图形展示：

除了使用以上指标进行分析，还可以通过图形直观展示数据情况。参数检验常用图形有：折线图、条形图等，非参数检验可以使用箱线图查看。

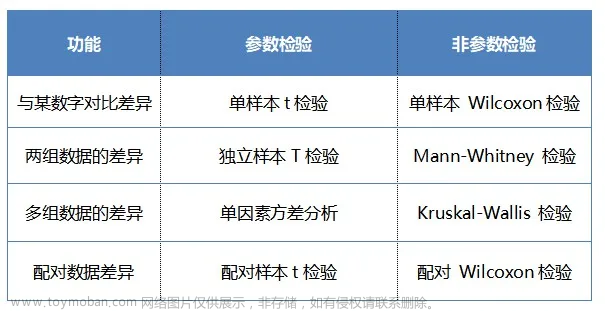
非参数检验——Wilcoxon 检验 & Friedman 检验与 Nemenyi 后续检验

折线图

非参数检验——Wilcoxon 检验 & Friedman 检验与 Nemenyi 后续检验

箱线图

参数检验与非参数检验的方法对比

凡是在分析过程中不涉及总体分布参数的检验方法，都可以称为“非参数检验”。因而，与参数检验一样，非参数检验包括许多方法。以下是最常见的非参数检验及其对应的参数检验对应方法：

非参数检验——Wilcoxon 检验 & Friedman 检验与 Nemenyi 后续检验

非参数检验的方法

非参数检验的方法是五花八门，名字也是千奇百怪，但是，这些方法有它们的共性。

上面介绍了，因为对总体的分布形态不清楚或总体分布不是正态分布，所以无法用参数检验来推断总体的集中趋势和离散程度的参数。

统计学家想到用排秩（排序）的方法来规避不是正态分布的问题，用样本的排序情况来推断总体的分布情况。这就好比梁山一百单八将排好了座次，从中随机抽出几个，测试武力值，大概其能够了解梁山的实力如何。

下图是非参数检验常用的检验方法表: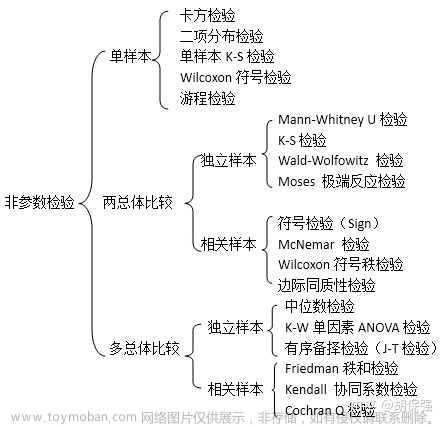
非参数检验——Wilcoxon 检验 & Friedman 检验与 Nemenyi 后续检验

Wilcoxon 检验

Frank Wilcoxon (1892—1965) 是美国的统计学家，发表了 70 篇左右论文，但其最大的贡献就是这 2 个以他名字命名的非参假设检验方法：秩和检验 和 符号秩检验。他在 1945 年发表的论文 1 中将二者分别称为 非成对检验 （unpaired experiment）和 成对检验（paired comparison）。正是因为其巨大影响力使得这两个检验方法都以他的名字命名，并流传下来。

Wilcoxon rank-sum test（秩和检验）

基本概念

在统计学中，Wilcoxon rank-sum test（威尔科克森秩和检验） 也叫 Mann-Whitney U test（曼-惠特尼 U 检验），或者 Wilcoxon-Mann-Whitney test。秩和检验是一个非参的假设检验方法，一般用来检测 2 个数据集是否来自于相同分布的总体。

这里的 “秩” 其实就是 “排名” 的意思，“秩和” 当然就是指 “将排名进行求和” 的操作。在秩和检验中，我们不要求被检验的 2 组数据包含相同个数的元素，换句话说，秩和检验更适用于非成对数据之间的差异性检测。

应用实例

假设我们有 2 组数据 $x_{1}$ 和 $x_{2}$ ，如下表所示， $x_{1}$ 中有 7 个元素（列 $x_1$ 中）， $x_{2}$ 中有 8 个元素（列 $x_{2}$ 中），现在使用秩和检验判断这 2 组数据是否存在显著性差异。

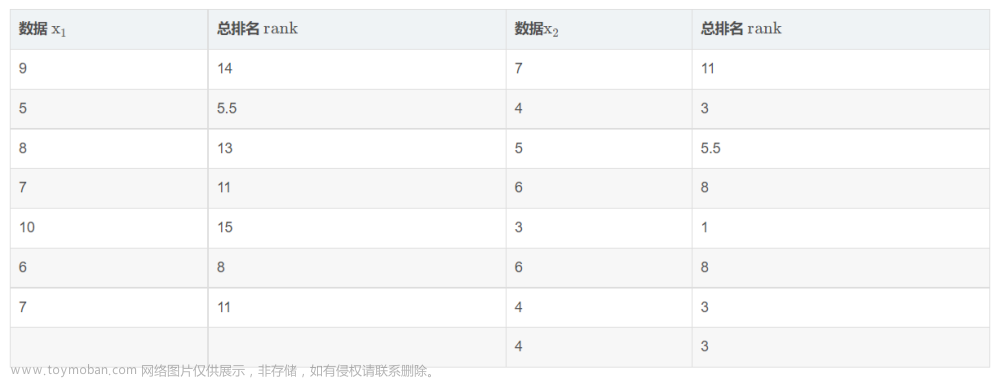
非参数检验——Wilcoxon 检验 & Friedman 检验与 Nemenyi 后续检验
步骤 1：我们首先将 $x_{1}$ 和 $x_{2}$ 整合成一个序列，并按升序重新排序，序号记在表中的 $r ank$ 列当中。我们分别计算 2 组数据的排名之和 $R_{1}$ 和 $R_{2}$ 有：

注意，当我们计算若干等值元素的排名时，会用这些元素排名的平均值作为它们在整个序列中的排名。例如 $x_{1}$ 中的第 2 个元素与 $x_{2}$ 中第3 个元素的值都等于 5，且这 2 个 5 在整个序列中的排名分别是第 5 和第 6，因此这两个元素的排名为 $\frac{5+6}{2}=5.5$ 。其余等值元素的排名计算也与之类似。

步骤 2：令 $n_{1}$ 和 $n_{2}$ 分别表示 2 组数据的个数，即 $n_{1}=7$ , $n_{2}=8$ 。再令 T TT 表示小样本的排名和，即 $T = R_1 = 77.5$ 。根据计算公式可得 $U_{1}$ 和 $U_{2}$ 的值如下：

非参数检验——Wilcoxon 检验 & Friedman 检验与 Nemenyi 后续检验
步骤 3：由于 $U_{1}$ 更小，我们依此来查 Wilcoxon 双尾临界表，当 $α = 0.05 , n_1 = 7 , n_2 = 8$ 时的临界值是 10。因为 $U_{1} < 10$ ，故应该拒绝原假设。

最终结论是： $x_{1}$ 和 $x_{2}$ 存在统计意义上的显著性差异，它们可能来自分布不同的总体。

编程实现

在 python 中我们调用 scipy 包来里的 stats.mannwhitneyu() 函数来实现秩和检验，如下代码：

from scipy import stats

x = [9,5,8,7,10,6,7]
y = [7,4,5,6,3,6,4,4]

def wilcoxon_rank_sum_test(x, y):
	res = stats.mannwhitneyu(x ,y)
	print(res)

wilcoxon_rank_sum_test(x, y)

wilcoxon_rank_sum_test(y, x)

非参数检验——Wilcoxon 检验 & Friedman 检验与 Nemenyi 后续检验

Wilcoxon signed-rank test（符号秩检验）

基本概念

Wilcoxon signed-rank test（威尔科克森符号秩检验）也是一种非参的假设检验方法，它成对的检查 2 个数据集中的数据（即 paired difference test）来判断 2 个数据集是否来自相同分布的总体。

应用实例

假设我们有 2 组数据 $y_{1}$ 和 $y_{2}$ ，如下表所示。我们按照如下 3 步来计算 wilcoxon signed-rank test 的结果。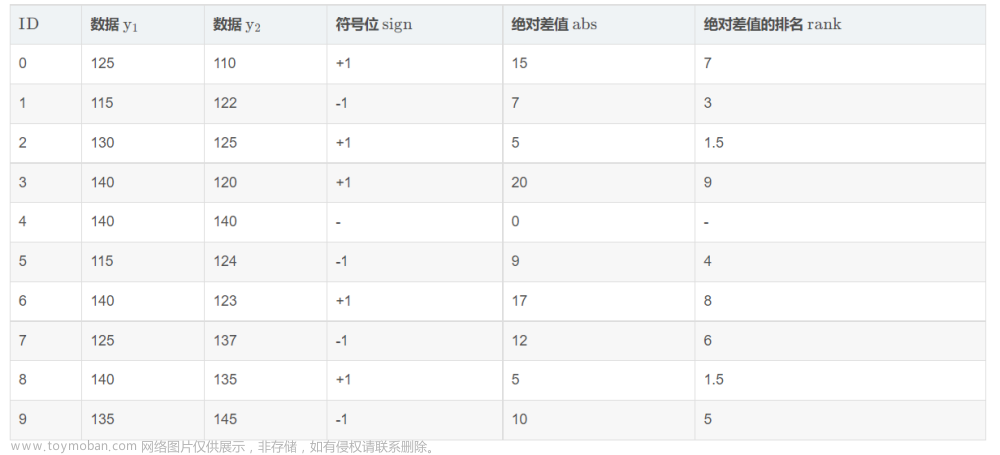
非参数检验——Wilcoxon 检验 & Friedman 检验与 Nemenyi 后续检验
步骤 1：首先对 $y_{1}$ 和 $y_{2}$ 两两成对配对形成 10 个数据对（即 $I D = 0, ..., 9$ ），然后将这 10 个数据对两两求差，得到符号位 $s i g n$ 列。具体的做法是：当 $y_1$ 元素比 $y_2$ 对应元素大时，符号位为正，即 $+ 1$ ；当 $y_1$ 元素比 $y_2$ 对应元素小时，符号位为负，即 $- 1$ 。例如，在 $I D = 1$ 的数据对中， $125 > 110$ ，故其符号位为 $+ 1$ .

步骤 2：首先对 $y_{1}$ 和 $y_{2}$ 两两成对求差得到绝对值 $ab s$ 列，然后根据 $ab s$ 列排序得到 $r ank$ 列。当某一对 $y_{1}$ 和 $y_{2}$ 的元素相等时，即 $ab s = 0$ 时，我们不计算其 $r ank$ 值。例如，在 $I D = 4$ 的数据对中， $y_1$ 和 $y_2$ 的值都是 140，因此这对数组没有排名值。

步骤 3：有了这个 $s i g n$ 和 $r ank$ 列的结果后，我们就可以来计算秩和了，其中大于 0 的秩和 $W^{+}$ 和对于小于 0 的秩和 $W^{-}$ ，以及最终的符号秩和 $∣ W ∣$ 如下所示，

非参数检验——Wilcoxon 检验 & Friedman 检验与 Nemenyi 后续检验
步骤 4：最后我们根据 $∣ W ∣$ 来查表，我们得到当 Wilcoxon 在 $\alpha=0.05$ $n = 9$ 的时候的临界值是 5，而我们计算出来的 $∣ W ∣ = 9 > 5$ ，因此我们不能拒绝原假设。最终结论是： $y_{1}$ 和 $y_{2}$ 不存在统计意义上的显著性差异，它们可能来自于同一分布的总体。

编程实现

在 python 中我们调用 scipy 包来里的 stats.wilcoxon() 函数来实现秩和检验，如下代码，

from scipy import stats

x = [125,115,130,140,140,115,140,125,140,135]
y = [110,122,125,120,140,124,123,137,135,145]

def wilcoxon_signed_rank_test(x, y):
	res = stats.wilcoxon(x ,y)
	print(res)

wilcoxon_signed_rank_test(x, y)

wilcoxon_signed_rank_test(y, x)

非参数检验——Wilcoxon 检验 & Friedman 检验与 Nemenyi 后续检验
得到的结果如下，其中 $s t a t i s t i c = 18.0$ ，表示 2 类符号秩和较小的一个（ $W^{+}$ 和 $W^{-}|$ 最小的是 $18$ ）； $p v a l u e = 0.5936 \dots$ 就是我们需要的 $p - v a l u e$ 值。之所以出现 Warning 信息是因为我们的数据量太少，一般来讲大于 $20$ 是比较合适做假设检验的。

非参数检验——Wilcoxon 检验 & Friedman 检验与 Nemenyi 后续检验

Wilcoxon 符号秩检验临界表

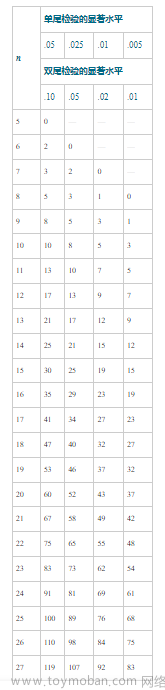
非参数检验——Wilcoxon 检验 & Friedman 检验与 Nemenyi 后续检验
2022年10月12日更新：
我太难了，又看到了Friedman算法，这是个啥，不知道啊，接着学习吧，记录一下！

Friedman 检验与 Nemenyi 后续检验

当我们提出一种算法，需要知道我们的算法和现在已有的算法相比，性能是否更优的时候，就需要用到模型性能评估的方法。

Friedman 检验与 Nemenyi 后续检验方法的特点是：可以进行多个算法的比较。

计算序值

假定我们用 $D_1、D_2、D_3$ 和 $D_4$ 四个数据集对算法 $A$ 、 $B$ 、 $C$ 进行比较。

首先需要得到每个算法在每个数据集上的测试结果，可以是准确率，也可以是均方误差，然后在每个数据上根据测试性能的好坏进行排序，并赋予序值 1，2，…。

如果算法的测试性能相同，则评分排名。
比如，在 $D_1$ 和 $D_3$ 上， $A$ 最好、 $B$ 次之， $C$ 最差，而在 $D_2$ 上 $A$ 最好 $B$ 和 $C$ 性能相同，…，则可以列出如下表所示的序值表，对每一列的序值进行求平均，得到平均序值。

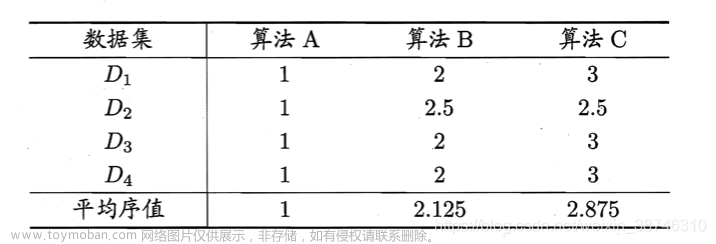
非参数检验——Wilcoxon 检验 & Friedman 检验与 Nemenyi 后续检验

Friedman 检验

使用 Friedman 检验来判断这些算法是否性能相同。如果相同，则他们的平均序值应该相等。

假定我们在 $N$ 个数据集上比较 $k$ 个算法，令 $r_i$ 表示第 $i$ 个算法的平均序值。为简化讨论，暂时不考虑平分序值的情况，则 $r_i$ 服从正态分布，其均值和方差分别为 $(k + 1) /2$ 和 $k^2-1)/12$ 。变量

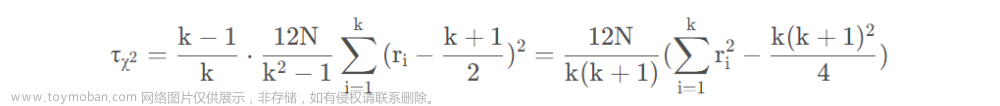
非参数检验——Wilcoxon 检验 & Friedman 检验与 Nemenyi 后续检验
在 $k$ 和 $N$ 都较大时，服从自由度为 $k - 1$ 的 $\chi^2$ 分布。

然后，上述的这样的 “原始 Friedman 检验” 过于保守，现在通常使用变量

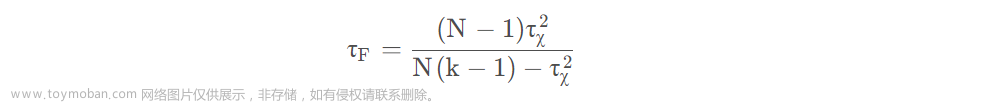
非参数检验——Wilcoxon 检验 & Friedman 检验与 Nemenyi 后续检验
其中， $\tau_F$ 服从自由度为 $k - 1$ 和 $(k - 1) (N - 1)$ 的 $F$ 分布。常用的临界值可以见下表。

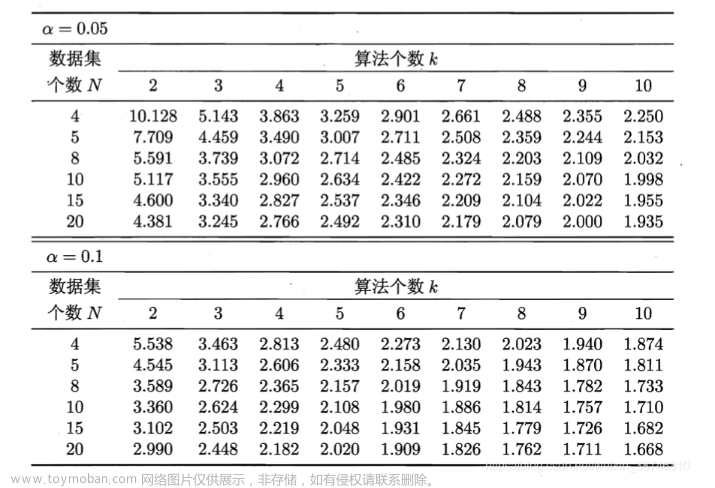
非参数检验——Wilcoxon 检验 & Friedman 检验与 Nemenyi 后续检验
若 “所有算法的性能相同” 这个假设被拒绝，则说明算法的性能显著不同。

Nemenyi 后续检验

这个时候就需要使用 “后续检验”（post-hoc test）来进一步区分算法。常用的算法是 Nemenyi 后续检验。

Nemenyi 检验计算出平均序值差别的临界值域

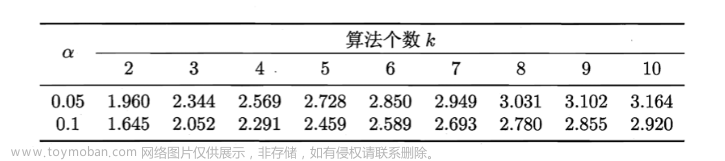
非参数检验——Wilcoxon 检验 & Friedman 检验与 Nemenyi 后续检验
下表给出了 $\alpha = 0.05$ 和 $0.1$ 时常用的 $q_\alpha$ 值。

若两个算法的平均序值之差超出了临界值域#CD# ，则以相应的置信度拒绝 “两个算法性能相同” 这一假设。

非参数检验——Wilcoxon 检验 & Friedman 检验与 Nemenyi 后续检验

Python实现

import numpy as np
import matplotlib.pyplot as plt
 
 
def Friedman(n, k, data_matrix):
    '''
    Friedman 检验
    :param n:数据集个数
    :param k: 算法种数
    :param data_matrix:排序矩阵
    :return:T1
    '''
 
    # 计算每个算法的平均序值
    row, col = data_matrix.shape  # 获取矩阵的行和列
    xuzhi_mean = list()
    for i in range(col):  # 计算平均序值
        xuzhi_mean.append(data_matrix[:, i].mean())  # xuzhi_mean = [1.0, 2.125, 2.875] list列表形式
    sum_mean = np.array(xuzhi_mean)  # 转成 numpy.ndarray 格式方便运算
 
    sum_ri2_mean = (sum_mean ** 2).sum()  # 整个矩阵内的元素逐个平方后，得到的值相加起来
    result_Tx2 = (12 * n) * (sum_ri2_mean - ((k * ((k + 1) ** 2)) / 4)) / (k * (k + 1))  # P42页的公式
    result_Tf = (n - 1) * result_Tx2 / (n * (k - 1) - result_Tx2)  # P42页的公式
    return result_Tf
 
 
def nemenyi(n, k, q):
    '''
    Nemenyi 后续检验
    :param n:数据集个数
    :param k:算法种数
    :param q:直接查书上2.7的表
    :return:
    '''
    cd = q * (np.sqrt((k * (k + 1) / (6 * n))))
    return cd
 
 
data = np.array([[1, 2, 3], [1, 2.5, 2.5], [1, 2, 3], [1, 2, 3]])
 
T1 = Friedman(4, 3, data)
cd = nemenyi(4, 3, 2.344)
print('tf={}'.format(T1))
print('cd={}'.format(cd))
 
# 画出CD图
row, col = data.shape  # 获取矩阵的行和列
xuzhi_mean = list()
for i in range(col):  # 计算平均序值
    xuzhi_mean.append(data[:, i].mean())  # xuzhi_mean = [1.0, 2.125, 2.875] list列表形式
sum_mean = np.array(xuzhi_mean)
# 这一句可以表示上面sum_mean： rank_x = list(map(lambda x: np.mean(x), data.T))  # 均值 [1.0, 2.125, 2.875]
name_y = ["A1", "A2", "A3"]
# 散点左右的位置
min_ = sum_mean - cd / 2
max_ = sum_mean + cd / 2
# 因为想要从高出开始画，所以数组反转一下
name_y.reverse()
sum_mean = list(sum_mean)
sum_mean.reverse()
max_ = list(max_)
max_.reverse()
min_ = list(min_)
min_.reverse()
# 开始画图
plt.title("Friedman")
plt.scatter(sum_mean, name_y)  # 绘制散点图
plt.hlines(name_y, max_, min_)
plt.show()