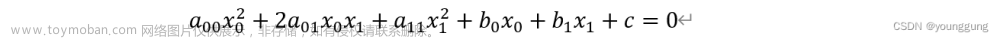ECC椭圆曲线入门-Toy模板网

这篇具有很好参考价值的文章主要介绍了ECC椭圆曲线入门。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

区块链学习网站

https://web3study.club/

简介

ECC(Ellipse Curve Cryptography)又称椭圆曲线密码体制、椭圆曲线加密算法等。椭圆曲线加密算法在比特币、区块链上有着广泛的应用。

公式： y^2 = x^3 + ax + b

这里使用简单易懂的方式对大家介绍这部分内容，让大家有个简单的理解

原理简介

公私钥加密内容

公钥未公开部分，私钥则是不可泄露的过程就是吧需要加密的信息用公钥进行加密，然后发送给私钥进行解密，且只有私钥可以进行解密这里就会牵扯出两个问题：

公钥加密的过程是快速的，且简单的
加密后的信息是不可逆的且直接进行解密是困难的，即不可逆。

图形讲解

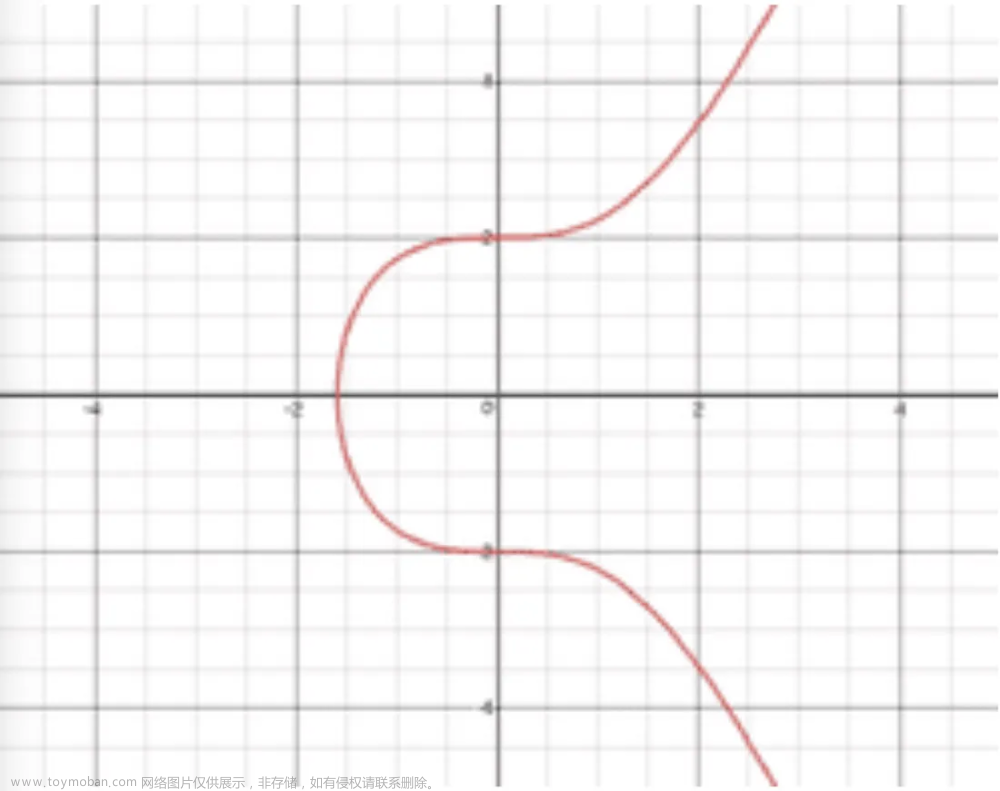
椭圆曲线示例：

ECC椭圆曲线入门

椭圆曲线是x轴对称的，在y轴正向随便选择一个点，-y一定会有一个对称点
随便在图形上找两个点，两个点连成线，然后延长会经过第三个点（垂直线除外）

ECC椭圆曲线入门

如图，A、B延长线之后，寻找y轴的对称点，会得到点C，即一个运算，A-B得到C 简单的说为点运算（此点运算就是椭圆曲线的加运算）：A点B=C

ECC椭圆曲线入门

连接AC，相交于一点，找到其对称点 D，即：A点C=D

依次类推，比如点E，再一次连接AE，可以找到更多的点

假设一个条件：已知起点为A、终点为F点，请问经过多少次点运算可以得到点F

ECC椭圆曲线入门

如果说给出路径来看的话，肯定是可以得出F点的点运算次数，但是如果没有的话就相当困难了，比如你打桌球，让你的朋友看到白球的起点，然后闭眼，你开始打，停到某个位置后告诉你朋友睁眼，问他：请问我打出白球的路线，这肯定是不知道的，包括有可能你自己都忘记了。这也就是其中的一个原则：正向容易，逆向难（加密简单，解密困难）

ECC椭圆曲线入门

但是有一个特例，比如说上图，点P是一个切点，延长线的对称点为Q点，切点可以当做是2个点的重合点，即P点P=Q = 2P 然后再次延长相交对称：P点2P=3P 再依次对称可以得到6P点，6P就很特殊了，只看此定义，可以这样： (3p)2 = 6P (2p)3 = 6p 乘法问题。

DH算法原理

简单举一个例子糖醋排骨，Alice和Bob都有一个独特的配方，Alice的糖，Bob的醋，Cindy是他们之间的联络员，但是Cindy总想偷他们的配方 Alice这里加糖处理好排骨之后，会通过Cindy发给Bob，Bob使用醋处理好排骨之后会通过Cindy发给Alice，这时候Cindy是没法获取完全的配方及成品的，然后Alice和Bob获得各自货物后，进行再加工，Alice加白糖，Bob加醋，就形成了糖醋排骨的原始材料，进行烹制后就是糖醋排骨了，这样就可以拿取卖了，这里会发现，Cindy虽然都接触到了，但是没有拿到核心的配方，也么有办法窃取他们的成果。

ECC椭圆曲线入门

其中排骨是公开的，这个就可以类比为公钥，Cindy因为没有其他人的私钥，所以最终也获取不到糖醋排骨。

在此基础上加上椭圆曲线算法

ECC椭圆曲线入门

Alice生成私钥a，Bob生成私钥b，
Alice和Bob都有一个公共的数据G，其是开放的，所有人都可以知道，然后Alice使用私钥经过a次点运算生成公钥A，Bob也是用生成公钥B
然后进行交换，A、B的运算就是使用的椭圆曲线加密运算，因为a次后生成A，这个次数是很难知道的，不可逆的，所以A是不能反向退出a的，相同的B也不能反向退出点b
互换之后，Alice产生一个新密钥，aB，Bob产生一个新密钥bA，然后根据刚才描述的(3p)2 = 6P问题，将aB与bA拆解：
1. aB = a(bG)
2. bA=b(aG) 其中就可以把 a(bG) = b(aG) ，即 aB = bA

ECDHE就是以上的椭圆曲线与DH混合起来的密钥交换算法，正向容易、逆向困难