1. Toy模板网首页
  2. > Toy博客

【数据结构入门】二叉树的遍历（前序、中序、后序、层序）

10月前 作者：平行线也会相交 分类：Toy博客 阅读(40) 违法举报

这篇具有很好参考价值的文章主要介绍了【数据结构入门】二叉树的遍历（前序、中序、后序、层序）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

个人主页：平行线也会相交
欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 平行线也会相交 原创
收录于专栏【数据结构初阶（C实现）】
【数据结构入门】二叉树的遍历（前序、中序、后序、层序）

二叉树遍历

什么是二叉树遍历：

二叉树遍历就是按照某种特定的规则，依次堆二叉树中的结点进行相应的操作，并且每个结点只操作一次。访问结点所做的操作依赖于具体的应用问题。遍历是二叉树上最重要的运算之一，也是二叉树上进行其它运算的基础。

我们以后看到二叉树应该这样去看待：把他看成根、左子树、右子树。

二叉树的遍历有：前序、中序、后序、层序遍历的递归结构遍历：

1.前序遍历（Preorder Traversal），也叫前根遍历：
2.中序遍历（Inorder Traversal），也叫中根遍历：
3.后序遍历（Post orderTraversal）也叫后根遍历：
4.层序遍历
【数据结构入门】二叉树的遍历（前序、中序、后序、层序）
【数据结构入门】二叉树的遍历（前序、中序、后序、层序）

前序遍历

下面是前序遍历的动态图。
【数据结构入门】二叉树的遍历（前序、中序、后序、层序）
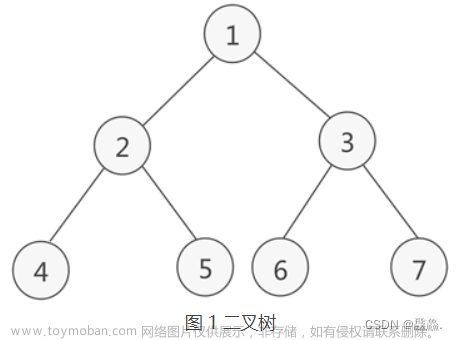
以下图为例进行代码的编写：
【数据结构入门】二叉树的遍历（前序、中序、后序、层序）
请看代码：

void PreOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	printf("%d ", root->data);
	PreOrder(root->left);
	PreOrder(root->right);
	
}

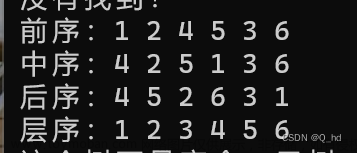
这是运行结果：
【数据结构入门】二叉树的遍历（前序、中序、后序、层序）

中序遍历

请看中序遍历的动态图：

【数据结构入门】二叉树的遍历（前序、中序、后序、层序）
还是以下图进行举例：
【数据结构入门】二叉树的遍历（前序、中序、后序、层序）
请看代码：

//中序遍历
void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	InOrder(root->left);
	printf("%d ", root->data);
	InOrder(root->right);
}

下面是运行结果：
【数据结构入门】二叉树的遍历（前序、中序、后序、层序）

后序遍历

下面是后序遍历的动态图：
【数据结构入门】二叉树的遍历（前序、中序、后序、层序）

还是以下图进行举例：
【数据结构入门】二叉树的遍历（前序、中序、后序、层序）

//后序遍历
void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%d ", root->data);
}

请看运行结果：
【数据结构入门】二叉树的遍历（前序、中序、后序、层序）

前中后序总代码

#define _CRT_SECURE_NO_WARNINGS 1

#include<stdio.h>
#include<stdlib.h>
#include<assert.h>

typedef int BTDataType;
typedef struct BinaryTreeNode
{
	BTDataType data;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;

//新建结点
BTNode* BuyNode(BTDataType x)
{
	BTNode* node = (BTNode*)malloc(sizeof(BTNode));
	if (node == NULL)
	{
		perror("malloc fail");
		return NULL;
	}
	node->data = x;
	node->left = NULL;
	node->right = NULL;

	return node;
}

BTNode* CreatTree()
{
	BTNode* node1 = BuyNode(1);
	BTNode* node2 = BuyNode(2);
	BTNode* node3 = BuyNode(3);
	BTNode* node4 = BuyNode(4);
	BTNode* node5 = BuyNode(5);
	BTNode* node6 = BuyNode(6);

	node1->left = node2;
	node1->right = node4;
	node2->left = node3;
	node4->left = node5;
	node4->right = node6;

	return node1;
}

//前序遍历
void PreOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	printf("%d ", root->data);
	PreOrder(root->left);
	PreOrder(root->right);
	
}

//中序遍历
void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	InOrder(root->left);
	printf("%d ", root->data);
	InOrder(root->right);
}

//后序遍历
void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%d ", root->data);
}

int main()
{
	BTNode* root = CreatTree();
	//PreOrder(root);//前序遍历
	//InOrder(root);//中序遍历
	//PostOrder(root);//后序遍历
	return 0;
}

最后，其实前序、中序、后序的过程基本上就是一样的，即前序、中序、后序的递归过程是一样的，不一样的就是访问根的时机不一样。

层序遍历

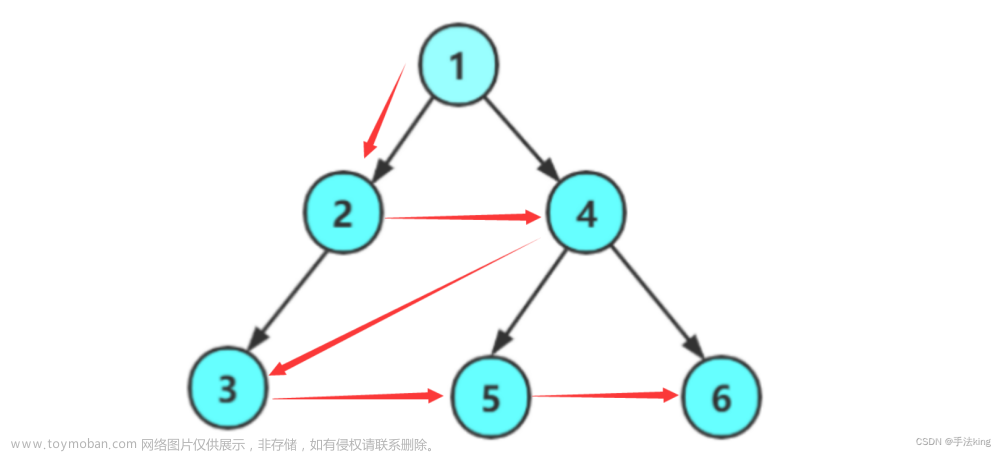
层序遍历的话可以利用队列先进先出的特点来进行实现，出上一层，带入下一层。
所以这里的层序遍历就是利用队列来实现的。
【数据结构入门】二叉树的遍历（前序、中序、后序、层序）
【数据结构入门】二叉树的遍历（前序、中序、后序、层序）

注意队列中的结点里面的data存的是树结点的指针。

层序遍历总代码

Queue.h

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>

typedef struct BinaryTreeNode* QDataType;

typedef struct QueueNode
{
	struct QueueNode* next;
	QDataType data;
}QueueNode;

typedef struct Queue
{
	QueueNode* head;
	QueueNode* tail;
}Queue;

void QueueInit(Queue* pq);

void QueueDestory(Queue* pq);

void QueuePush(Queue* pq,QDataType x);//插入数据

void QueuePop(Queue* pq);//删除数据

QDataType QueueFront(Queue* pq);//取队头的数据

QDataType QueueBack(Queue* pq);//取队尾的数据

int QueueSize(Queue* pq);//有多少个数据

bool QueueEmpty(Queue* pq);//判断队列是否为空

Queue.c

#define _CRT_SECURE_NO_WARNINGS 1
#include"Queue.h"

//初始化
void QueueInit(Queue* pq)
{
	assert(pq);
	pq->head = NULL;
	pq->tail = NULL;
}

void QueueDestory(Queue* pq)
{
	assert(pq);
	QueueNode* cur = pq->head;
	while (cur)
	{
		QueueNode* next = cur->next;
		free(cur);
		cur = cur->next;
	}
	pq->head = pq->tail = NULL;
}

void QueuePush(Queue* pq, QDataType x)
{
	assert(pq);
	QueueNode* newnode = (QueueNode*)malloc(sizeof(QueueNode));
	newnode->data = x;
	newnode->next = NULL;
	if (pq->head == NULL)
	{
		pq->head = pq->tail = newnode;
	}
	else
	{
		pq->tail->next = newnode;
		pq->tail = newnode;
	}
}

//删除
void QueuePop(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));
	//if (pq->head == NULL)
	//{
	//	return;
	//}//温柔的处理
	QueueNode* next = pq->head->next;
	free(pq->head);
	pq->head = next;
	if (pq->head == NULL)
	{
		pq->tail=NULL;
	}
}

bool QueueEmpty(Queue* pq)
{
	assert(pq);
	return pq->head == NULL;
}

QDataType QueueBack(Queue* pq)//取队尾的数据
{
	assert(pq);
	assert(!QueueEmpty(pq));
	return pq->tail->data;
}

QDataType QueueFront(Queue* pq)//取队头的数据
{
	assert(pq);
	assert(!QueueEmpty(pq));
	return pq->head->data;
}

int QueueSize(Queue* pq)//有多少个数据
{
	assert(pq);
	int n = 0;
	QueueNode* cur = pq->head;
	while (cur)
	{
		n++;
		cur = cur->next;
	}
	return n;
}

test.c

#define _CRT_SECURE_NO_WARNINGS 1

#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include"Queue.h"


typedef int BTDataType;
typedef struct BinaryTreeNode
{
	BTDataType data;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;

//新建结点
BTNode* BuyNode(BTDataType x)
{
	BTNode* node = (BTNode*)malloc(sizeof(BTNode));
	if (node == NULL)
	{
		perror("malloc fail");
		return NULL;
	}
	node->data = x;
	node->left = NULL;
	node->right = NULL;

	return node;
}

BTNode* CreatTree()
{
	BTNode* node1 = BuyNode(1);
	BTNode* node2 = BuyNode(2);
	BTNode* node3 = BuyNode(3);
	BTNode* node4 = BuyNode(4);
	BTNode* node5 = BuyNode(5);
	BTNode* node6 = BuyNode(6);

	node1->left = node2;
	node1->right = node4;
	node2->left = node3;
	node4->left = node5;
	node4->right = node6;

	return node1;
}

//前序遍历
void PreOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	printf("%d ", root->data);
	PreOrder(root->left);
	PreOrder(root->right);
	
}

//中序遍历
void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	InOrder(root->left);
	printf("%d ", root->data);
	InOrder(root->right);
}

//后序遍历
void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%d ", root->data);
}

int size = 0;

求树中结点个数法1
//int TreeSize(BTNode* root,int* psize)
//{
//	if (root == NULL)
//		return;
//	(*psize)++;
//	TreeSize(root->left, psize);
//	TreeSize(root->right, psize);
//}

//求树的结点个数法2
int TreeSize(BTNode* root)
{
	return root == NULL ? 0 :
		TreeSize(root->left)
		+ TreeSize(root->right)
		+ 1;
}

//求树的高度
int TreeHeight(BTNode* root)
{
	if (root == NULL)
		return 0;
	int leftHeight = TreeHeight(root->left);
	int rightHeight = TreeHeight(root->right);

	return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}


int TreeKLevel(BTNode* root, int k)
{
	if (root == NULL)
		return 0;
	if (k == 1)
		return 1;
	int leftK = TreeKLevel(root->left, k - 1);
	int rightK = TreeKLevel(root->right, k - 1);

	return leftK + rightK;
}

//二叉树查找值为x的结点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
	if (root == NULL)
		return NULL;
	if (root->data == x)
		return root;
	BTNode* lret = BinaryTreeFind(root->left, x);
	if (lret)
		return lret;
	BTNode* rret = BinaryTreeFind(root->right, x);
	if (rret)
		return rret;
	return NULL;
}

//层序遍历
void LevelOrder(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	if (root)
		QueuePush(&q, root);
		
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		//front指向的不是队列的结点，而是树的结点
		QueuePop(&q);
		printf("%d ", front->data);

		if (front->left)
			QueuePush(&q, front->left);
		if (front->right)
			QueuePush(&q, front->right);
	}
	QueueDestory(&q);
}

int main()
{
	BTNode* root = CreatTree();
	//PreOrder(root);//前序遍历
	//InOrder(root);//中序遍历
	//PostOrder(root);//后序遍历


	求树的结点法1
	/*int size1 = 0;
	TreeSize(root, &size1);
	printf("TreeSize:%d\n", size1);

	int size2 = 0;
	TreeSize(root, &size2);
	printf("TreeSize:%d\n", size2);*/


	求树的结点法2
	//printf("TreeSize:%d\n", TreeSize(root));
	//printf("TreeSize:%d\n", TreeSize(root));
	//printf("TreeSize:%d\n", TreeSize(root));


	求树的高度
	//printf("TreeHeight:%d\n", TreeHeight(root));

	//printf("TreeKLevel:%d\n", TreeKLevel(root, 1));
	
	二叉树查找值为x的结点
	//printf("BinaryTreeFind:%p\n", BinaryTreeFind(root, 5));
	//printf("BinaryTreeFind:%p\n", BinaryTreeFind(root, 0));

	//层序遍历
	LevelOrder(root);

	return 0;
}

【数据结构入门】二叉树的遍历（前序、中序、后序、层序）

以上就是二叉树遍历的四种方式（前序、中序、后序、层序）。说实话，内容还是有些难度的，这就更需要我们认真的进行学习并复习了。
加油，各位！！！文章来源地址https://www.toymoban.com/news/detail-408463.html

到了这里，关于【数据结构入门】二叉树的遍历（前序、中序、后序、层序）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处： 如若内容造成侵权/违法违规/事实不符，请点击违法举报进行投诉反馈，一经查实，立即删除！

分享到：
领支付宝红包 赞助服务器费用

相关文章

  • 数据结构与算法-二叉树的遍历

    数据结构与算法-二叉树的遍历

    🌞 “少年没有乌托邦，心向远方自明朗！” 二叉树的遍历是按照一定次序访问二叉树中的所有结点，且每个结点仅被访问一次的过程。遍历线性结构是容易解决的，而二叉树的结构是非线性结构，需要寻找规律，使二叉树的结点排列在一个线性队列上，便于遍历。 由二叉树

    2024年02月08日
    浏览(46)
  • 数据结构——二叉树的遍历与应用

    数据结构——二叉树的遍历与应用

    目录 一.前言 二. 二叉树链式结构的实现 2.1 前置说明 2.2 二叉树的遍历 2.2.1 前序、中序以及后序遍历 前序遍历： 中序遍历递归图： 后序遍历： 2.3节点个数 2.4叶子节点个数 2.5第K层的节点个数 2.6 二叉树查找值为x的节点 2.7 二叉树的销毁 三.结语   大家好久不见，放寒假了咱

    2024年01月19日
    浏览(47)
  • 【数据结构】二叉树的层序遍历

    【数据结构】二叉树的层序遍历

    当我们面对一个树结构时，常常需要对其进行遍历以获取其中的节点信息。其中一种常用的遍历方式是层序遍历，也称为广度优先搜索（BFS）。本篇博客将详细介绍层序遍历的原理和实现方法。 层序遍历以树的根节点开始，按照从上到下、从左到右的顺序逐层遍历树中的节点

    2024年02月03日
    浏览(45)
  • Java数据结构——二叉树的遍历

    Java数据结构——二叉树的遍历

     作者：敲代码の流川枫 博客主页：流川枫的博客 专栏：和我一起学java 语录：Stay hungry stay foolish 工欲善其事必先利其器，给大家介绍一款超牛的斩获大厂offer利器——牛客网 点击注册和我一起刷题 文章目录 1.创建二叉树 2.二叉树的三种遍历方式 3.代码实现遍历 前序遍历

    2024年01月22日
    浏览(49)
  • 数据结构——二叉树的创建与遍历（链式存储结构）

    数据结构——二叉树的创建与遍历（链式存储结构）

    二叉树（binary tree）是指树中节点的度不大于2的有序树，它是一种最简单且最重要的树。二叉树的递归定义为：二叉树是一棵空树，或者是一棵由一个根节点和两棵互不相交的，分别称作根的左子树和右子树组成的非空树；左子树和右子树又同样都是二叉树。以下是对链式存

    2024年02月05日
    浏览(51)
  • 【C语言 数据结构】二叉树的遍历

    【C语言 数据结构】二叉树的遍历

    所谓先序遍历二叉树，指的是从根结点出发，按照以下步骤访问二叉树的每个结点： 访问当前结点； 进入当前结点的左子树，以同样的步骤遍历左子树中的结点； 遍历完当前结点的左子树后，再进入它的右子树，以同样的步骤遍历右子树中的结点； 先序遍历这棵二叉树的过

    2024年02月04日
    浏览(45)
  • 【数据结构】二叉树的链式实现及遍历

    【数据结构】二叉树的链式实现及遍历

    后文所有代码中的二叉树结点： 前，中，后序遍历都可以采用分治递归的思想解决，将根节点和它的孩子结点分别处理。 此处仅利用递归展开图分析前序遍历，中序和后序也是相同的思想： 层序遍历需要利用队列来进行，如果二叉树跟结点不为空，则让 指向它的一个指针入

    2024年02月07日
    浏览(50)
  • 数据结构——二叉树的遍历【前序、中序、后序】

    数据结构——二叉树的遍历【前序、中序、后序】

    hello hello~ ，这里是大耳朵土土垚~💖💖 ，欢迎大家点赞🥳🥳关注💥💥收藏🌹🌹🌹 💥 个人主页：大耳朵土土垚的博客 💥 所属专栏：数据结构学习笔记 、C语言系列函数实现 💥对于数据结构顺序表、链表、堆有疑问的都可以在上面数据结构的专栏进行学习哦~ 有问题可

    2024年03月15日
    浏览(54)
  • 【数据结构】二叉树的层序遍历（四）

    【数据结构】二叉树的层序遍历（四）

     目录 一，层序遍历概念 二，层序遍历的实现         1，层序遍历的实现思路         2，创建队列         Queue.h         Queue.c         3，创建二叉树         BTree.h         BTree.c         4，层序遍历的实现 层序遍历：除了先序遍历、中序遍历、

    2024年02月07日
    浏览(47)
  • 【数据结构】二叉树的前序遍历（七）

    【数据结构】二叉树的前序遍历（七）

    题目详情： 给你二叉树的根节点 root ，返回它节点值的  前序   遍历； 我们先来看几个示例： 输入：root = [ 1，null，2，3 ] 输出：[ 1，2，3 ]  示例2： 输入：root = [ 1，2 ] 输出：[ 1，2 ] 示例三： 输入：root = [  ] 输出：[  ] 提示： 树中结点数目在范围【0，100】内 -100 = Nod

    2024年02月07日
    浏览(43)

觉得文章有用就打赏一下文章作者

支付宝扫一扫打赏

博客赞助

微信扫一扫打赏

请作者喝杯咖啡吧~博客赞助

支付宝扫一扫领取红包，优惠每天领

二维码1

领取红包

二维码2

领红包