目录
2.1 矩阵的创建
2.1.1 直接输入:
2.1.2 载入外部数据文件
2.1.3 利用内置函数创建
2.2 矩阵的寻访
2.2.1 下标元素访问
2.2.2 访问单元素
2.3 矩阵的拼接
2.3.1 矩阵拼接符[]
2.3.2 函数
2.4 矩阵的运算
2.4.1 加减
2.4.2 乘除
2.4.3乘方
2.4.4 按位运算
2.4.5 行列式与秩
2.4.6 逆与迹
2.4.7 矩阵的范数(?)
2.4.8 特征值和特征向量
PS 纯纯用来记笔记,要是有错随时dd我呀
2.1 矩阵的创建
2.1.1 直接输入:
(1)矩阵元素必须在[]内
(2)同行元素用,/空格 分隔
(3)不同行元素用; 分隔
eg
C=[1 2 3; 5 6; 7 8 9]
2.1.2 载入外部数据文件
Load函数
eg
创建一个data.txt 内容为 1 2 3 4 5 6 7 8 9 0
在Matlab中读取:
clear all;
load trees %读取二进制数据文件
image(X) %以图像的形式显示数组X
colormap(X) %设置颜色查找表为map2.1.3 利用内置函数创建
| 函数名 | 功能介绍 |
| ones() | 全1矩阵 |
| zeros() | 全0矩阵 |
| eye() | 单位矩阵 |
| rand() | (0,1)之间的随机矩阵 |
| randn() | 均值0,方差1的随机矩阵 |
| compan | 伴随矩阵 |
| gallery | Higham 检验矩阵 |
| hadamard | hadamard阵 |
| hankel | hankel阵 |
| hilb | hilbert阵 |
| invhilb | 逆hilbert阵 |
| magic | 魔方阵 |
| pascal | pascal阵 |
| rosser | 经典对称特征阵 |
| toeplitz | toeplitz阵 |
| vander | vander阵 |
| wilknsion | wilknsion特征值检验矩阵 |
eg
Z1=ones(3)
z1= 1 1 1
1 1 1
1 1 12.2 矩阵的寻访
2.2.1 下标元素访问
(1)双下标 “第几行,第几列”
(2)单下标 “以列为单位,将元素凑成一行”
| 1 | 4 |
| 2 | 5 |
| 3 | 6 |
(3) 双下标计算单下标 sub2ind(元素总数,行,列)
单下标计算双下标 ind2sub
2.2.2 访问单元素
M=(行,列)
2.2.3 访问多元素
(1)以元素为单位
A(e1:e2:e3) 表示矩阵第e1个元素,隔e2个元素一直到e3的所有元素
A([m n 1]) 表示取矩阵A中第m,n,1个元素
(2)以行 列为单位
A(i,:) 取第i行
A(:,j) ..列
A(i,i+m,:) 取i~i+m行
A(:,j,j+m) ...列
A(i,i+m,k,k+j) 取i~i+m,k~k+k
2.3 矩阵的拼接
!!维数必须相同
2.3.1 矩阵拼接符[]
水平 C=[A,B] C=[A B]
竖直 C=[A;B]
2.3.2 函数
(1)cat 函数
C=cat(dim,A,B)
dim=1(垂直),2(水平),3(三维数组)
(2)repmat函数
C=repmat(A,m,n)/C=repmat(A,[m,n])
C是由A拼接而成,纵向m个A,横向n个A


(3) horzcat 函数
!!必须有相同的行数
C=horzcat(A,B,..) 进行水平拼接

(4) vertcat 函数
!!必须有相同的列数
C=vertcat(A,B)
(5)blkdiag 函数
构造块对角矩阵
T=blkdiag(A,B,C,D)
eg
>> clear all;
>> A=eye(2);
>> B=ones(2,2);
>> C=[1 2;3 4;5 6];
>> D=magic(3);
>> T=blkdiag(A,B,C,D)
2.4 矩阵的运算
2.4.1 加减
C=A+B
C=A-B
2.4.2 乘除
(1)乘(矩阵的笛卡尔乘)

C=A*B(A叉乘B)
(2)除(乘法的逆运算)
\ 左除
/ 右除
2.4.3乘方
!!矩阵A是方阵
A^x 矩阵A的x乘方
2.4.4 按位运算
按位乘(.*) 按位右除(./) 按位左除(.\)
2.4.5 行列式与秩
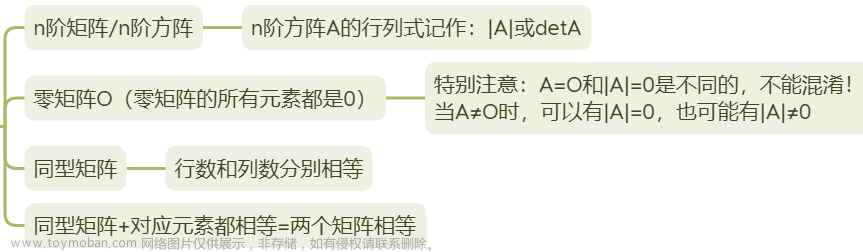
(1)行列式 det
矩阵的行列式是一个数值
det(A)
(2)秩 rank
如果把矩阵看成一个个行向量或者列向量,秩就是这些行向量或者列向量的秩,也就是极大无关组中所含向量的个数。
rank(A)
2.4.6 逆与迹
(1)逆矩阵 inv
设A是一个n阶矩阵,若存在另一个n阶矩阵B,使得: AB=BA=E(E为单位矩阵) ,则称方阵A可逆,并称方阵B是A的逆矩阵。
inv(A)
(2)矩阵的迹 trace
矩阵的迹等于矩阵的特征值之和。
trace(A)
2.4.7 矩阵的范数(?)
cond(A,1) 表示计算A的1-范数下的条件数
cond(A) 表示计算A的2-范数下的条件数
cond(A,inf) 表示计算A的无限-范数下的条件数
2.4.8 特征值和特征向量
(1)定义:
设A是n阶方阵,如果数λ和n维非零列向量x使关系式Ax=λx成立,那么这样的数λ称为矩阵A特征值,非零向量x称为A的对应于特征值λ的特征向量。
式Ax=λx也可写成( A-λE)X=0,这是n个未知数n个方程的齐次线性方程组,它有非零解的充分必要条件是系数行列式| A-λE|=0。
(2)
E=eig(B) 求矩阵的全部特征值,构成向量E
[V,D]=eig(B) 对角阵D:B的全部特征值
矩阵V:B的特征向量构成V的列向量
2.4.9 矩阵的超越函数
!!输入参数必须为方阵
sqrt,exr,log类似功能并且直接作用于矩阵上的
sqrtm(A) 计算矩阵的平方根
logm 矩阵对数文章来源:https://www.toymoban.com/news/detail-408636.html
expm 矩阵指数文章来源地址https://www.toymoban.com/news/detail-408636.html
到了这里,关于Matlab 数字图像 第二章 矩阵及其运算的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!