二叉树相关操作---纯代码实现详解

目录

前言 (很重要)

二叉树的概念

二叉树的相关术语

相关操作菜单

  二叉树的构造

 创建二叉树

先序遍历二叉树  

 中序遍历二叉树

 后序遍历二叉树

 层次遍历二叉树

 二叉树的深度

 二叉树的叶子结点数

 二叉树的结点数

整体代码

结果展示

结束语

前言 (很重要)

        大家好，今天给大家带来的是二叉树的相关操作，希望能够给大家带来帮助。

        另外有很多小伙伴们在学习算法的时候，只去学习一些关于算法理论的知识，并不知道自己的代码实战能力如何，也不清楚到底对该算法的了解有多深，所以在这里小张给大家推荐一个很棒的平台，在这里有很多的面试和算法题，也有很多的面试和求职的机会，大家可以点击下方链接进入牛客网刷算法真题，提高自己代码实战能力，早日拿到满意的offer！点击这里进入牛客网刷算法和面试真题提高代码实战能力

二叉树的概念

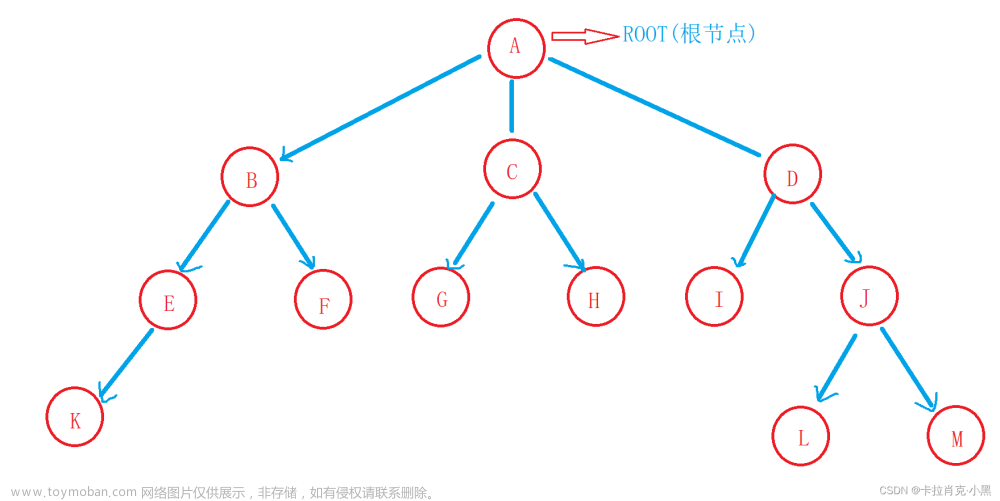
        二叉树（Binary tree）是树形结构的一个重要类型。许多实际问题抽象出来的数据结构往往是二叉树形式，即使是一般的树也能简单地转换为二叉树，而且二叉树的存储结构及其算法都较为简单，因此二叉树显得特别重要。二叉树特点是每个节点最多只能有两棵子树，且有左右之分 。

二叉树的相关术语

①节点：包含一个数据元素及若干指向子树分支的信息 。

②节点的度：一个节点拥有子树的数目称为节点的度 。

③叶子节点：也称为终端节点，没有子树的节点或者度为零的节点 。

④分支节点：也称为非终端节点，度不为零的节点称为非终端节点 。

⑤树的度：树中所有节点的度的最大值 。

⑥节点的层次：从根节点开始，假设根节点为第1层，根节点的子节点为第2层，依此类推，如果某一个节点位于第L层，则其子节点位于第L+1层 。

⑦树的深度：也称为树的高度，树中所有节点的层次最大值称为树的深度  。

相关操作菜单

//菜单
void menu()
{
	cout << "\t\t\t******************************************************************" << endl;
	cout << "\t\t\t****************  1.输入-1  退出程序           *******************" << endl;
	cout << "\t\t\t****************  2.输入1   初始化二叉树       *******************" << endl;
	cout << "\t\t\t****************  3.输入2   对二叉树先序遍历   *******************" << endl;
	cout << "\t\t\t****************  4.输入3   对二叉树中序遍历   *******************" << endl;
	cout << "\t\t\t****************  5.输入4   对二叉树后序遍历   *******************" << endl;
	cout << "\t\t\t****************  6.输入5   对二叉树层次遍历   *******************" << endl;
	cout << "\t\t\t****************  7.输入6   二叉树深度         *******************" << endl;
	cout << "\t\t\t****************  8.输入7   二叉树叶子结点数   *******************" << endl;
	cout << "\t\t\t****************  9.输入8   二叉树的结点数     *******************" << endl;
	cout << "\t\t\t******************************************************************" << endl;
}

  二叉树的构造

//构造二叉树
typedef struct Binode
{
	//数据域
	char data;
	//定义左孩子和右孩子
	struct Binode*lchid, *rchid;
}Binode, *StrBinode;

 创建二叉树

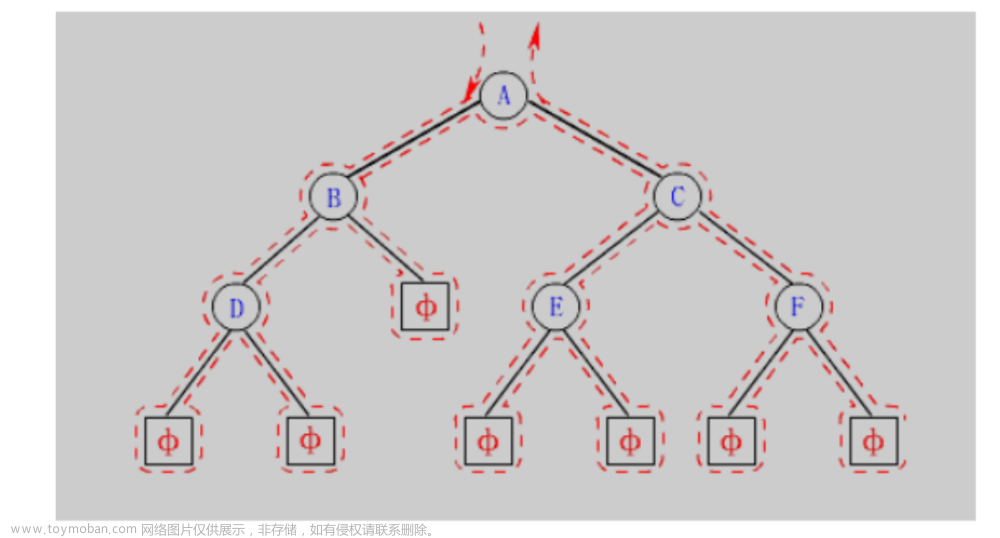
//先序遍历创建二叉树
void creatBinode(StrBinode&T)
{
	cin >> ch;
	if (ch == '#')
	{
		//如果输入是#的话就说明根结点就是叶子结点
		//就没必要再去进行开辟一个二叉树空间
		T = NULL;
	}
	else
	{
		T = new Binode;
		T->data = ch;
		creatBinode(T->lchid);
		creatBinode(T->rchid);
	}
}

先序遍历二叉树  

//先序遍历二叉树
void visitBinode(StrBinode&T)
{
	if (T!=NULL)
	{
		cout << T->data << " ";
		visitBinode(T->lchid);
		visitBinode(T->rchid);
	}
	if(T==NULL)
	{
		cout << "#" << " ";
	}
}

 中序遍历二叉树

//中序遍历二叉树
void MidvisitBinode(StrBinode&T)
{
	if (T != NULL)
	{
		visitBinode(T->lchid);
		cout << T->data << " ";
		visitBinode(T->rchid);
	}
	if (T == NULL)
	{
		cout << "#" << " ";
	}
}

 后序遍历二叉树

//后序遍历二叉树
void BackvisitBinode(StrBinode&T)
{
	if (T != NULL)
	{
		visitBinode(T->lchid);
		visitBinode(T->rchid);
		cout << T->data << " ";
	}
	if (T == NULL)
	{
		cout << "#" << " ";
	}
}

 层次遍历二叉树

//二叉树的层次遍历
void Levelorder(StrBinode&HT)
{
	StrBinode T;
	T = new Binode;
	//创建一个队列qu
	queue<StrBinode> qu;
	//将根结点的指针压入队列
	qu.push(HT);
	//当队列不为空的时候就继续进行循环
	while (!qu.empty())
	{
		//让T里面存放队列中第一个元素的值
		T = qu.front();
		//C++自带的队列出队的话是删除值不返回值
		qu.pop();
		//访问出队元素的值
		cout << T->data << " ";
		//当该节点左孩子不为空的时候就让左孩子入队
		if (T->lchid != NULL)
		{
			qu.push(T->lchid);
		}
		//当该节点右孩子不为空的时候就让左孩子入队
		if (T->rchid != NULL)
		{
			qu.push(T->rchid);
		}
	}
	
}

 二叉树的深度

//二叉树的深度
int deep(StrBinode&T)
{
	if (T == NULL)
	{
		return 0;
	}
	else
	{
		int m = deep(T->lchid);
		int n = deep(T->rchid);
		if (m > n)
		{
			return (m + 1);
		}
		else
		{
			return (n + 1);
		}
	}
}

 二叉树的叶子结点数

//求二叉树的叶子结点
int leaf(StrBinode&T)
{
	//如果是空树
	if (T == NULL)
	{
		//返回0
		return 0;
	}
	//如果是叶子结点
	if (T->lchid == NULL && T->rchid == NULL)
	{
		//返回1
		return 1;
	}
	return leaf(T->lchid) + leaf(T->rchid);
}

 二叉树的结点数

//求二叉树的结点数
int Nodecount(StrBinode&T)
{
	//如果是根结点没有数据
	if (T == NULL)
	{
		return 0;
	}
	else
	{
		return Nodecount(T->lchid) + Nodecount(T->rchid) + 1;
	}
}

整体代码

#include<iostream>
#include<queue>
using namespace std;
char ch = 0;

//构造二叉树
typedef struct Binode
{
	//数据域
	char data;
	//定义左孩子和右孩子
	struct Binode*lchid, *rchid;
}Binode, *StrBinode;

//先序遍历创建二叉树
void creatBinode(StrBinode&T)
{
	cin >> ch;
	if (ch == '#')
	{
		//如果输入是#的话就说明根结点就是叶子结点
		//就没必要再去进行开辟一个二叉树空间
		T = NULL;
	}
	else
	{
		T = new Binode;
		T->data = ch;
		creatBinode(T->lchid);
		creatBinode(T->rchid);
	}
}

//先序遍历二叉树
void visitBinode(StrBinode&T)
{
	if (T!=NULL)
	{
		cout << T->data << " ";
		visitBinode(T->lchid);
		visitBinode(T->rchid);
	}
	if(T==NULL)
	{
		cout << "#" << " ";
	}
}

//中序遍历二叉树
void MidvisitBinode(StrBinode&T)
{
	if (T != NULL)
	{
		visitBinode(T->lchid);
		cout << T->data << " ";
		visitBinode(T->rchid);
	}
	if (T == NULL)
	{
		cout << "#" << " ";
	}
}

//后序遍历二叉树
void BackvisitBinode(StrBinode&T)
{
	if (T != NULL)
	{
		visitBinode(T->lchid);
		visitBinode(T->rchid);
		cout << T->data << " ";
	}
	if (T == NULL)
	{
		cout << "#" << " ";
	}
}

//二叉树的层次遍历
void Levelorder(StrBinode&HT)
{
	StrBinode T;
	T = new Binode;
	//创建一个队列qu
	queue<StrBinode> qu;
	//将根结点的指针压入队列
	qu.push(HT);
	//当队列不为空的时候就继续进行循环
	while (!qu.empty())
	{
		//让T里面存放队列中第一个元素的值
		T = qu.front();
		//C++自带的队列出队的话是删除值不返回值
		qu.pop();
		//访问出队元素的值
		cout << T->data << " ";
		//当该节点左孩子不为空的时候就让左孩子入队
		if (T->lchid != NULL)
		{
			qu.push(T->lchid);
		}
		//当该节点右孩子不为空的时候就让左孩子入队
		if (T->rchid != NULL)
		{
			qu.push(T->rchid);
		}
	}
	
}

//二叉树的深度
int deep(StrBinode&T)
{
	if (T == NULL)
	{
		return 0;
	}
	else
	{
		int m = deep(T->lchid);
		int n = deep(T->rchid);
		if (m > n)
		{
			return (m + 1);
		}
		else
		{
			return (n + 1);
		}
	}
}

//求二叉树的叶子结点
int leaf(StrBinode&T)
{
	//如果是空树
	if (T == NULL)
	{
		//返回0
		return 0;
	}
	//如果是叶子结点
	if (T->lchid == NULL && T->rchid == NULL)
	{
		//返回1
		return 1;
	}
	return leaf(T->lchid) + leaf(T->rchid);
}

//求二叉树的结点数
int Nodecount(StrBinode&T)
{
	//如果是根结点没有数据
	if (T == NULL)
	{
		return 0;
	}
	else
	{
		return Nodecount(T->lchid) + Nodecount(T->rchid) + 1;
	}
}

//菜单
void menu()
{
	cout << "\t\t\t******************************************************************" << endl;
	cout << "\t\t\t****************  1.输入-1  退出程序           *******************" << endl;
	cout << "\t\t\t****************  2.输入1   初始化二叉树       *******************" << endl;
	cout << "\t\t\t****************  3.输入2   对二叉树先序遍历   *******************" << endl;
	cout << "\t\t\t****************  4.输入3   对二叉树中序遍历   *******************" << endl;
	cout << "\t\t\t****************  5.输入4   对二叉树后序遍历   *******************" << endl;
	cout << "\t\t\t****************  6.输入5   对二叉树层次遍历   *******************" << endl;
	cout << "\t\t\t****************  7.输入6   二叉树深度         *******************" << endl;
	cout << "\t\t\t****************  8.输入7   二叉树叶子结点数   *******************" << endl;
	cout << "\t\t\t****************  9.输入8   二叉树的结点数     *******************" << endl;
	cout << "\t\t\t******************************************************************" << endl;
}

int main()
{
	int n = 0;
	StrBinode T;
	menu();
	while (cin >> n)
	{
		if (n < 0)
		{
			break;
		}
		switch (n)
		{
		case 1:
			//初始化二叉树
			cout << "请输入值对二叉树进行初始化" << endl;
			creatBinode(T);
			cout << "初始化完成" << endl;
			break;
		case 2:
			//先序遍历
			cout << "先序遍历的结果为" << endl;
			visitBinode(T);
			cout << "先序遍历结束" << endl;
			break;
		case 3:
			//中序遍历
			cout << "中序遍历的结果为" << endl;
			MidvisitBinode(T);
			cout << "中序遍历结束" << endl;
			break;
		case 4:
			//后序遍历
			cout << "后序遍历的结果为" << endl;
			BackvisitBinode(T);
			cout << "后序遍历结束" << endl;
			break;
		case 5:
			//层次遍历
			cout << "层次遍历的结果为" << endl;
			Levelorder(T);
			cout << "层次遍历结束" << endl;
			break;
		case 6:
			cout << "二叉树的深度为：";
			cout << deep(T) << endl;
			break;
		case 7:
			cout << "二叉树的叶子结点数为：";
			cout << leaf(T) << endl;
			break;
		case 8:
			cout << "二叉树的结点数为；";
			cout << Nodecount(T) << endl;
			break;
		default:
			cout << "您的输入有误，请重新输入" << endl;
			break;
		}
	}
	return 0;
}

结果展示

结束语

        到这里今天的内容就已经全部结束了，这里的代码是运用C++语言实现的，其他语言的话也大同小异，只要相关的思想掌握了，就能写出来相应的代码，最后小张在这里感谢大家的支持 ！文章来源地址https://www.toymoban.com/news/detail-408755.html

到了这里，关于二叉树相关操作---纯代码实现详解的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！