目录
前言
1. 二叉树的遍历
1.1二叉树的前、中、后序遍历
1.2 层序遍历
2.二叉树的实现
2.1 二叉树的结构
2.2构建二叉树
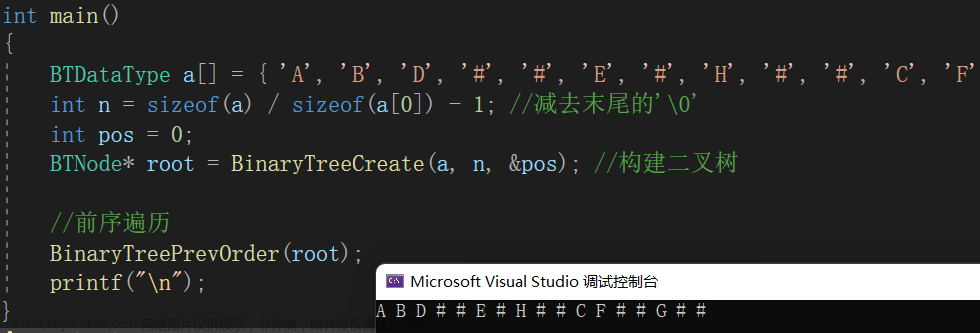
2.2 前序遍历的实现
2.3 中序遍历的实现
2.4 后序遍历的实现
2.5 计算树的节点个数
2.6 计算树的深度
2.7 计算叶子节点个数
2.8 计算树第k层的节点数
2.9 以内容查询树内的某个节点
2.10 层序遍历
2.11 判断是否为完全二叉树
3. 功能测试
前言
之前给大家介绍了有关堆的实现,那么这里小编就给大家带来今天的重头戏——二叉树的实现,以及介绍。
1. 二叉树的遍历
在介绍二叉树的实现之前,小编需要给大家给大家介绍一下二叉树遍历的几种方式,对于二叉树遍历(Traversal)是按照某种特定的规则,依次对二叉 树中的节点进行相应的操作,并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。 遍历 是二叉树上最重要的运算之一,也是二叉树上进行其它运算的基础。
1.1二叉树的前、中、后序遍历


这里我们的每一次递归都会访问一个新的节点,根据前序遍历规则,我们这里先访问根节点(也即是我们每次递归先访问的节点),然后再访问左树,最后访问右树,递归结束条件也就是当我们访问到了空节点。
1.2 层序遍历

2.二叉树的实现
由于在介绍堆的时候我们已经给大家介绍了二叉树的相关概念,所以这里小编就不再多加以介绍了,对二叉树相关概念不是很明白的可以翻看小编之前对堆有关介绍的文章。
2.1 二叉树的结构
之前我们在实现堆的时候由于堆是一棵完全二叉树,所以可以很好的使用数组对其进行存储,且不会造成大幅度的空间浪费,但是利用顺序表进行普通二叉树的存储,很可能会出现下面这种情况:

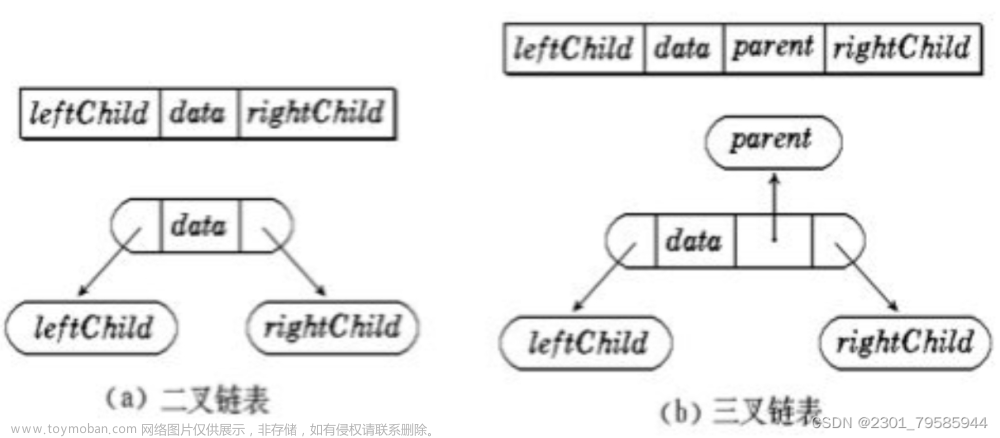
所以我们这里采用链表的方式对其进行存储,那么我们需要实现的链表的结构是:
typedef int BTDataType;
typedef struct BinaryTreeNode
{
BTDataType data;
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
}BTNode;
在介绍遍历之前,我先给大家讲接一下遍历的递归返回值的理解——对于遍历递归的函数返回,第一是当我们遇到空节点,这里我们以经没有往下访问的必要了,我们应该返回上一层函数(也就是我们访问这个节点的父节点位置),进行其他的操作,第二是我们的函数调用完毕,那么对这颗我们理解上的”新树“已经访问结束,就要返回上一层函数,进行相关操作。
2.2构建二叉树
由于二叉树的增删操作的意义不大,所以对于二叉树节点的控制我们一般是手动控制,那么直接看代码
BTNode* BuyNode(BTDataType x)
{
BTNode* node = (BTNode*)malloc(sizeof(BTNode));
if (node == NULL)
{
perror("malloc fail");
return NULL;
}
node->data = x;
node->left = NULL;
node->right = NULL;
return node;
}
BTNode* CreatTree()
{
BTNode* node1 = BuyNode(1);
BTNode* node2 = BuyNode(2);
BTNode* node3 = BuyNode(3);
BTNode* node4 = BuyNode(4);
BTNode* node5 = BuyNode(5);
BTNode* node6 = BuyNode(6);
BTNode* node7 = BuyNode(7);
node1->left = node2;
node1->right = node4;
node2->left = node3;
node4->left = node5;
node4->right = node6;
node3->right = node7;
return node1;
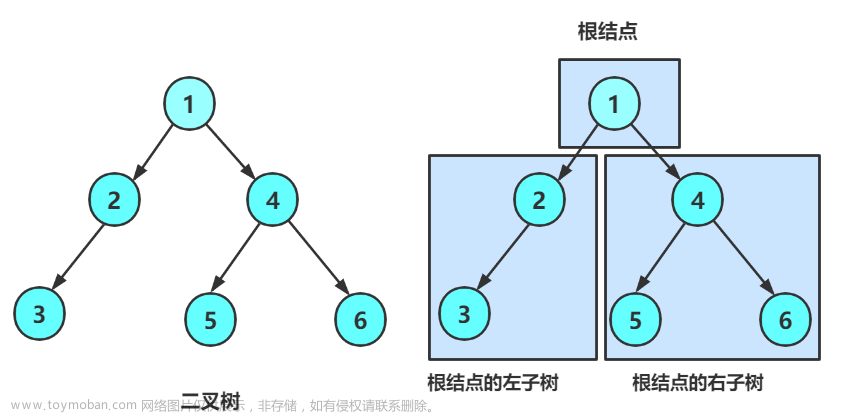
}首先我们写一个构造节点的函数,随后我们构造七个节点,然后利用树这个结构的左右指针,构造出我们所需要的结构,这里我构造的树是

2.2 前序遍历的实现
前面小编给大家简单的说明了前序遍历的遍历规则,以及该访问过程,那么我们用代码进行具体实现的过程是
void preorder(BTNode* root)
{
if (root == NULL)
{
return;
}
printf("%d ", root->data);
preorder(root->left);
preorder(root->right);
}可能大家这里有点迷惑,这短短的几行代码是怎么做到树的前序遍历的,这里我给大家简单的画一下递归展开图,以便大家更好的理解:

首先我们还是以这个树作为例子给大家画一下递归展开图:
 (图中红线表示函数的递归调用,绿线表示函数向上返回,序号表示函数的调用次序)
(图中红线表示函数的递归调用,绿线表示函数向上返回,序号表示函数的调用次序)
从这里我们可以看出我们先从根节点进访问,然后通过函数的递归调用,不断进行打印节点值,先访问左子树,再访问右子树的操作,我们这里把新访问的节点理解为新访问树的根,这里我们进行的就是先打印根的值,然后再访问左子树,再访问右子树。不断的进行此类操作就实现了前序遍历。
2.3 中序遍历的实现
中序遍历和前序遍历的思路一致,只是我们进行的操作是先访问左子树,在打印访问节点的函数值,最后再执行访问右子树。
代码如下:
void Inorder(BTNode* root)
{
if (root == NULL)
{
return;
}
Inorder(root->left);
printf("%d ", root->data);
Inorder(root->right);
}递归展开图如下:

(图中红线表示函数的递归调用,绿线表示函数向上返回,序号表示函数调用次序)
这里我们可以看到展开之后每次都是先访问左节点之后,再对内容进行打印,也就是我们从左子树返回到上一层也就是该父节点位置(可以理解为分解出来的新树的根),然后进行打印操作,访问右子树后,把访问的节点理解为我们新树的根,然后对该树的左子树进行操作,直到左子树被访问完了后,打印这个节点(也就是我们新访问的右子树的那个节点)。这样不断递归就可以达到我们中序遍历的效果。
2.4 后序遍历的实现
后序遍历的规则是,先访问左节点,再访问右节点,最后访问根节点,这里我们代码实现如下
void PostOrder(BTNode* root)
{
if (root == NULL)
{
return;
}
PostOrder(root->left);
PostOrder(root->right);
printf("%d ", root->data);
}递归展开图如下:

根据递归展开图,我们可以看到我们这里是左右子树都访问到空节点,然后开始打印,那么函数的返回过程也就是我们打印的过程,而这个过程也是从左子树开始,然后右子树,所以就可以的得到这里的访问顺序是左子树,右子树,根。
2.5 计算树的节点个数
这里我们先看代码:
int TreeSize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
return TreeSize(root->left) + TreeSize(root->right) + 1;
}这里我们的采用的是的思想是分治思想,而分治思想就是把一个大问题分解为类似的小问题,而这我们往往是采用递归的方式的实现的,那么这里的的思路是,一个树的节点等于它的左子树的节点个数加上它的右子树节点个数,再加上该本身,而对于其左子树和右子树,我们可以看作是一棵新的树,该值也等于该左子树的节点树加上该右子树节点数加上本身,我们不断套用这个思想就可以解决此类方法。那么这里我给大家演示一下。

这里的我画的只是一个函数递归的返回过程,这里只有遇到空节点才会返回,由于我们这里是的返回是带值的,所以这里会得到我们下一层的返回值也即是该左右孩子中的某个值。对于递归展开图这里我就不给大家画了,大家可以自己尝试一下,慢慢自己去理解递归的神奇。
2.6 计算树的深度
对于计算树的深度我们还是采用的是分治的思想,那么我们该如何让思考呢,首先我们把关注点放在根,左子树,右子树上,那么的到一棵树的深度和左子树,右子树和根有什么关系呢?其实不难发现一棵树的高度等于左子树和右子树中最深的子树加上根节点的高度。
具体代码如下:
int TreeHeight(BTNode* root)
{
if (root == NULL)
{
return 0;
}
int left = TreeHeight(root->left);//得到左子树深度
int right = TreeHeight(root->right);//得到右子树深度
return left > right ? left + 1 : right + 1;//对比左右子树深度,深度较深的+1
}这里的模拟图如下:

这里我也只是给大家画了一个返回图,大家可以自行带入函数中画出函数展开图,去理解。
对于此处大家可能还有另外一种写法:
int TreeHeight(BTNode* root)
{
if (root == NULL)
{
return 0;
}
return TreeHeight(root->left) > TreeHeight(root->right) ? TreeHeight(root->left)+ 1 :
TreeHeight(root->right)+ 1;//对比左右子树深度,深度较深的+1
}这里的逻辑虽然是正确的,但是我们却在重复的进行我们已经进行了的递归操作,首先我们要遍历左右子树,比较左右子树哪棵树的深度较深,首先我们需要重新递归遍历得到较深的树的高度值,那么从某种意义上来讲我们是重复遍历了我们已经遍历的树了。所以在遍历树之后我们需要用一个变量记住左右子树的深度,那么就避免了重复访问的问题。
2.7 计算叶子节点个数
这里我们采取的也是分治的思想,相信在经过前两道题的讲解,大家对于分治思想已经有了初步的了解,那么我们这里的思考是,我们的叶子节点等于左子树+右子树的叶子节点个数,那么我们怎么判断叶子节点呢?在了解过叶子节点的特征我们可以知道,叶子节点没有孩子节点。
这里的代码如下:
int BinaryTreeLeafSize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
int leftn = BinaryTreeLeafSize(root->left);
int rightn = BinaryTreeLeafSize(root->right);
if (root->left == NULL && root->right == NULL)
{
return leftn+rightn + 1;
}
return leftn + rightn;
}对于计算叶子节点的个数,为了避免递归的重复访问,我们还是采取用变量记录值的方法,这里返回图如下。

大家可以依据这个过程去理解递归。
2.8 计算树第k层的节点数
这里我们采用的思想还是分治思想,那么这里我们的思路如下
得到一棵树第k层节点数,相当于是我们得到左子树的第k-1层的节点数加上右子树的第k-1层节点数,那么我的代码如下:
int TreeLevel(BTNode* root, int k)
{
if (root == NULL)
{
return 0;
}
if (k == 1)
{
return 1;
}
return TreeLevel(root->left, k - 1) + TreeLevel(root->right, k - 1);
}那么我们这里还需要考虑到两个情况:
情况一:也就是我们的第k层大于树的深度,那么这里势必会访问到空节点,那么我们只需要在空节点就返回即可,如果k大于树的深度,那么我们返回的值也是0。如果是我们需要统计的那一层某个节点的某个孩子是空节点,那么我们返回的是那个空节点返回的值加上1,这里也是不影响我们统计第k层节点数的。
情况二:当k=1时,我们此时访问的也是第k层的节点,那么我们一访问到第k层的节点就需要返回1。
这里的返回图我浅显的给大家画一下

大家配合代码以及递归展开图理解一下。
2.9 以内容查询树内的某个节点
这里我相信大家已经猜到了,我们这里采用的还是分治思想,那么我们这里的思路是:从左右子树出发对节点进行访问,访问到我们的节点内容就返回该节点地址,否者返回空。
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
if (root == NULL)
{
return NULL;
}
BTNode* leftn = BinaryTreeFind(root->left, x);
if (leftn)
{
return leftn;
}
BTNode* rightn = BinaryTreeFind(root->right, x);
if (rightn)
{
return rightn;
}
return NULL;
}那么我们这里开始访问的是左子树,这里每次对访问的节点进行记录,其次我们这里就会对记录值进行判断,如果为空,不进行返回,则说明我们访问到了空节点,如果不为空则说明我们已经找到了我们所需要的节点,那么这里就会返回我们所需要的值,如果将左右子树遍历我结束,还没有获得我们所查找值,那么就会返回空。
返回图如下:

大家可以自己画一画递归展开图理解一下。
2.10 层序遍历
对于层序遍历我们这里需要使用到我们之前编写的队列这个结构,我们这里的思路是,出上一层,入下一层。那么这里就能合理的将树按照层序遍历的方式进行数据访问。在使用之前我们需要进行一个操作就是我们需要构建一个存储树这种节点的队列,至于队列的介绍,大家可以翻看小编主页的另外一篇文章。那么这里的代码如下:
void BinaryTreeLevelOrder(BTNode* root)
{
Queue q;
QueueInit(&q);
QueuePush(&q,root);
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
printf("%d ", front->data);
if (front->left)
{
QueuePush(&q, front->left);
}
if (front->right)
{
QueuePush(&q, front->right);
}
}
QueueDestroy(&q);
}但是这里由于我们存储的是树的节点,所以我们需要将队列的存储元素类型改为我们树的指针类型。
如下:
typedef struct BinaryTreeNode* QDataType;//存储类型修改成树的结构的指针类型
typedef struct QListNode
{
struct QListNode* _pNext;
QDataType _data;
}QNode;
// 队列的结构
typedef struct Queue
{
QNode* _front;
QNode* _rear;
int size;
}Queue;这里具体的过程我举例一组例子给大家看看具体过程:

这里大家配合代码理解一下。
2.11 判断是否为完全二叉树
由于这里我们判断一棵树是二叉树或者为完全二叉树,那么我们就要利用完全二叉树的特殊性,这里我们可以发现我们利用层序遍历,完全二叉树的空节点是连续的,那么我们就可以利用这点来判断完全二叉树。
但是这里我们与上面的层序遍历不一致,这里由于我们要判断空是否连续,所以我们需要把空节点也入队列,那么这里我们入队列的判断条件就与我们上方的层序遍历不一致。
这里先给大家看代码,我再给大家讲解代码思路
bool BinaryTreeComplete(BTNode* root)
{
//思路完全二叉树按层序走,非空节点一定是连续的
Queue q;
QueueInit(&q);
QueuePush(&q, root);
BTNode* front;
while (!QueueEmpty(&q))//入队列中的的节点,如果访问到空节点就结束循环
{
front = QueueFront(&q);
QueuePop(&q);
if (front == NULL)
{
break;
}
QueuePush(&q, front->left);
QueuePush(&q, front->right);
}
while (!QueueEmpty(&q))//访问到空节点的元素,就不断出队列,直到队列为空还没有访问到除空节点
//以外的节点,说明是完全二叉树,否则不是
{
QueuePop(&q);
front = QueueFront(&q);
if (front != NULL)
{
QueueDestroy(&q);
return false;
}
}
QueueDestroy(&q);
return true;
}这里我给大家分别举一个例子,大家理解一下:
普通二叉树:

完全二叉树:

这里我们发现我们遇到NULL后出队列的所有元素都是空节点,因此这时完全二叉树。
3. 功能测试
int main()
{
BTNode* root = CreatTree();
preorder(root);
printf("\n");
Inorder(root);
printf("\n");
PostOrder(root);
printf("\n");
printf("%d", TreeSize(root));
printf("\n");
printf("%d", TreeHeight(root));
printf("\n");
printf("%d", TreeLevel(root, 4));
printf("%p\n", BinaryTreeFind(root, 5));
printf("%p\n", BinaryTreeFind(root, 50));
printf("叶子节点个数是%d\n", BinaryTreeLeafSize(root));
BinaryTreeLevelOrder(root);
printf("\n");
printf("%d", BinaryTreeComplete(root));
return 0;
}
这里我们利用我们构建的二叉树将所有我们实现的功能进行测试,这里我们看结果。文章来源:https://www.toymoban.com/news/detail-409066.html
 文章来源地址https://www.toymoban.com/news/detail-409066.html
文章来源地址https://www.toymoban.com/news/detail-409066.html
到了这里,关于数据结构之二叉树的实现的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!