奇异值分解（SVD）和图像压缩-Toy模板网

这篇具有很好参考价值的文章主要介绍了奇异值分解（SVD）和图像压缩。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

在本文中，我将尝试解释 SVD 背后的数学及其几何意义，还有它在数据科学中的最常见的用法，图像压缩。

奇异值分解（SVD）和图像压缩

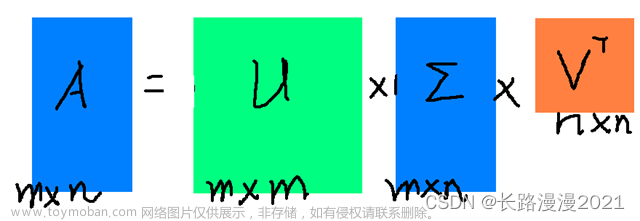
奇异值分解是一种常见的线性代数技术，可以将任意形状的矩阵分解成三个部分的乘积：U、S、V。原矩阵A可以表示为：

奇异值分解（SVD）和图像压缩

具体来说，A矩阵中的奇异值就是\Sigma矩阵中的对角线元素，它们是矩阵A的特征值的平方根，表示A矩阵在各个主方向上的拉伸程度。U矩阵是AA^{T的特征向量构成的正交矩阵，表示数据集在降维后的新的坐标系中的投影。V矩阵是A}TA的特征向量构成的正交矩阵，表示每个数据点在降维后的新坐标系中的坐标。

一个矩阵的奇异值（singular values）是指其奇异值分解中的\Sigma矩阵的对角线上的元素，也就是特征值的平方根。换句话说，矩阵的奇异值是矩阵的奇异值分解中量度矩阵对输入矩阵进行的线性变换的尺度因子。

奇异值在很多应用中都有广泛的应用，例如在图像处理中，它可以用来对图像进行压缩和降噪；在推荐系统中，它可以用来对用户的偏好进行建模和推荐相关的产品或服务；在自然语言处理中，它可以用来对文本数据进行降维和特征提取等。

数学原理

如果我们有一个矩阵A

要计算 SVD，首先需要通过找到 AA^{T} 的特征值来计算奇异值。

奇异值分解（SVD）和图像压缩

上述矩阵的特征方程为：

奇异值分解（SVD）和图像压缩

所以得到的奇异值是：

奇异向量就是 ATA 的正交特征向量集。ATA 的特征值是 25、9 和 0，由于 ATA 是对称的，我们知道特征向量是正交的。

所以，先计算 λ=25

奇异值分解（SVD）和图像压缩

然后进行化简：

奇异值分解（SVD）和图像压缩

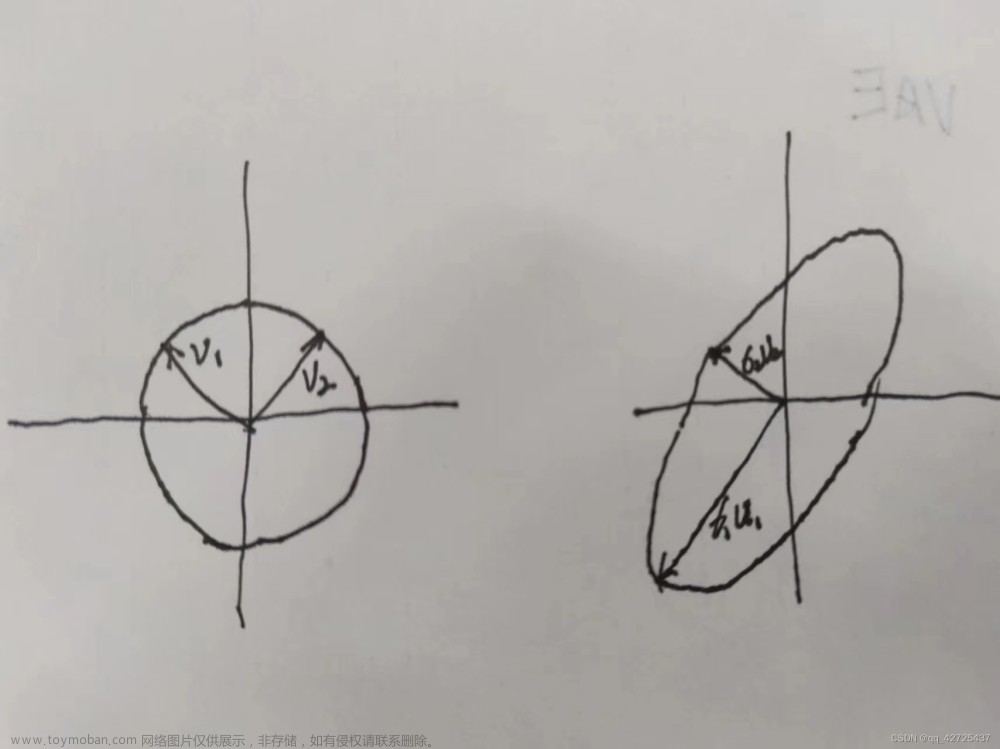
其方向的单位向量为：

奇异值分解（SVD）和图像压缩

同理对于 λ = 9，特征向量为：

奇异值分解（SVD）和图像压缩

对于第三个特征向量 0，我们可以使用它垂直于 v1 和 v2 的属性：

奇异值分解（SVD）和图像压缩

求解上述方程得到第三个特征向量

奇异值分解（SVD）和图像压缩

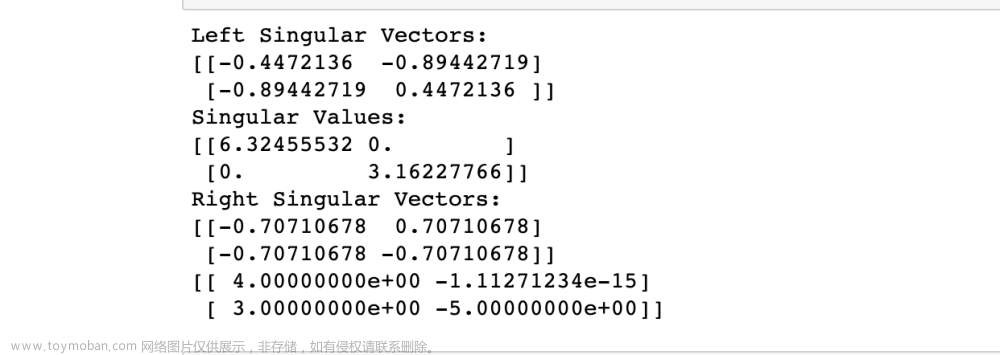
现在，我们计算 U，得到

奇异值分解（SVD）和图像压缩

这样就得到了最终的 SVD 方程：

奇异值分解（SVD）和图像压缩

图像压缩

通过仅保留最重要的奇异值及其对应的奇异向量，SVD 被用于图像压缩以减小图像的大小。这可以从根本上减少在不丢失其最重要的视觉数据的情况下存储图像所需的额外存储量。

我们将使用下面的图像进行图像压缩：

奇异值分解（SVD）和图像压缩

导入库和读取图片十分简单

 import requests
 import cv2
 import numpy as np
 import matplotlib.pyplot as plt
 
 img = cv2.imread('flower.bmp')
 gray_image = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
 gray_image = gray_image.astype(np.float64)

这里我们将图像转换成灰度图，执行奇异值分解

 U, s, V = np.linalg.svd(gray_image, full_matrices=False)

奇异值分解（SVD）和图像压缩

numpy中就包含了该方法，所有我们直接调用即可，我们看看前 10 个奇异值

 top_10_singular_values = s[:10]

奇异值分解（SVD）和图像压缩

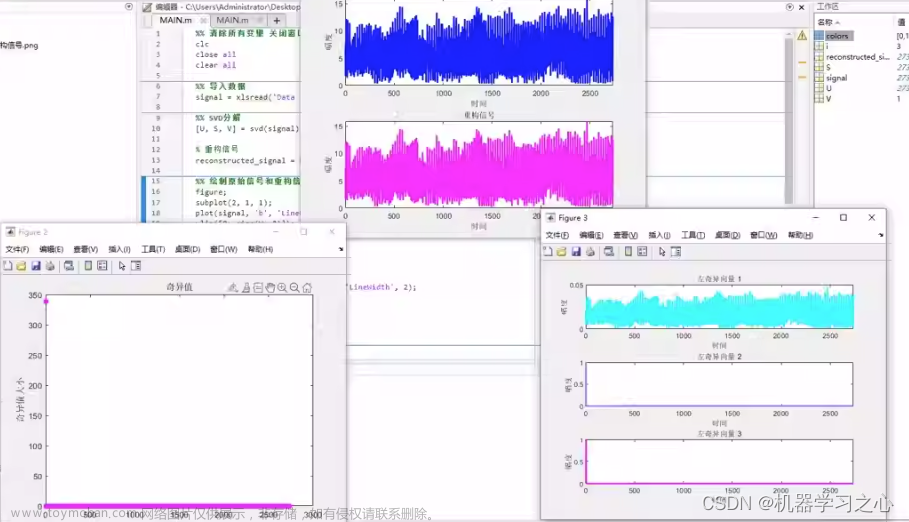
可视化

 plt.plot(range(1, len(s) + 1), s, 'r-')
 plt.xlabel("Rankings")
 plt.ylabel("Singular Values")
 plt.title("Singular Values versus their Rankings")
 plt.savefig("Singular_values_vs_rankings.png")
 plt.show()

奇异值分解（SVD）和图像压缩

从奇异值和排序图中可以注意到图像的大部分值都包含在少量奇异值中，所以可以得出到较高的奇异值包含的图像信息水平非常低，这也说明使用奇异值分解进行降维和图像压缩是可行的。

现在，让我们尝试重建和显示图像。

 k_values = [10, 50, 100]
 
 plt.figure(figsize=(12,6))
 
 for i in range(len(k_values)):
     low_rank = U[:, :k_values[i]] @ np.diag(s[:k_values[i]]) @ V[:k_values[i], :]
     plt.subplot(2,3,i+1),
     plt.imshow(low_rank, cmap='gray'),
     plt.title(f"For K value = {k_values[i]}")
     plt.savefig("Reconstruction_with_k_values.png")

奇异值分解（SVD）和图像压缩

可以注意到具有不同 K 值的所有图像都有显着差异。使用了前 10 个奇异值，结果图像一点也不清晰。使用了前 50 个奇异值，生成的图像比之前的图像清晰多了，但是还有一些轻微的模糊。当我们使用前 100 个奇异值时，图像比前两张图像越来越清晰，基本和原图很接近了。随着 K 值的增加，图像的清晰度也会增加。