题目:
内容:稀疏矩阵运算器
要求:使用三元组顺序表存储矩阵;实现矩阵的逆置、加、减、乘运算;具有相应的报错处理。
本人采用C++来书写该数据结构的题目,有兴趣的同学可以了解一下需要掌握一定的封装的能力。
类的结果存储如下所示:
class ju{
struct shu{
int i,j;
int x;
};
int m,n;
int len;
shu a[25];
public:
int juzhen[10][10]; //矩阵内容的存储
ju(int o,int p); //矩阵的初始化赋值
void print()const;
void generate(); //保存转置后的矩阵
void get_three(); //获得计算结束的三元组
int get_m()const;
int get_n()const;
ju Invert(ju y,ju c); //转置函数
ju& add(ju c,ju &y); //矩阵加法
ju& minus(ju c,ju &y); //矩阵减法
ju& multi(ju c,ju &y); //矩阵乘法
};加减法的函数内容如下所示:
其中的运算最容易实现的就是加减法,本人采取类成员函数的方式来进行计算,使用一个类的引用使其可以在函数体内部对其本身进行修改返回一个引用值可以避免程序开辟一个临时变量来浪费内存。具体的实现内容则是进行循环将其相应位置进行加减法的运算即可
ju & ju::add(ju c,ju &y)
{
int m1,n1;
m1=c.get_m();
n1=c.get_n();
if(m!=m1||n!=n1){
cout<<"您输入的矩阵格式不匹配\n";
return *this;
}
for(int i=1;i<=m;i++)
{
for(int j=1;j<=n;j++)
{
y.juzhen[i][j]=juzhen[i][j]+c.juzhen[i][j];
}
}
return y;
}
ju & ju::minus(ju c,ju &y)
{
int m1,n1;
m1=c.get_m();
n1=c.get_n();
if(m!=m1||n!=n1){
cout<<"您输入的矩阵格式不匹配\n";
return *this;
}
for(int i=1;i<=m;i++)
{
for(int j=1;j<=n;j++)
{
y.juzhen[i][j]=juzhen[i][j]-c.juzhen[i][j];
}
}
return y;
} 乘法的函数如下:
该函数实现的功能是矩阵的乘法,我们在线性代数中学习到的只有当前一项的列等于后一项的行时才可以进行相关的乘法,并且乘法规律则是第一行乘以第一列并且求和等于结果矩阵的1,1位置第一行乘以对应相乘第二列并且求和等于1.2位置以此类推。大家可以在纸上进行验算之后可知需要三次循环来存储结果的内容,其内容如下所示。
ju& ju::multi(ju c,ju &y)
{
if(n!=c.m)
cout<<"您输入的格式存在问题无法进行计算\n";
for(int i=1;i<=m;i++)
{
for(int j=1;j<=c.n;j++)
{
for(int k=1;k<=c.m;k++)
y.juzhen[i][j]+=juzhen[i][k]*c.juzhen[k][j];
}
}
return y;
}下来是转置并且保存结果矩阵的:
下面是稀疏矩阵的快速转置的实现,我们首先要定义两个数组来存储每一列具有多少个元素并且记录该列将转置到三元组的第几个位置,num数组则是存储一列具有多少个元素,position将记录转置到第几个位置。generate()则是获取存储该结果的矩阵。

void ju::generate()
{
int k,i,j;
juzhen[10][10]={0};
for(k=1;k<=len;k++){
i=a[k].i;
j=a[k].j;
juzhen[i][j]=a[k].x;
}
}
ju ju::Invert(ju y,ju c)
{
int a,b;
int num[20],position[20];
for(a=1;a<=c.len;a++)
{
num[a]=0;
position[a]=0;
}
for(a=1;a<=c.m;a++)
{
for(b=1;b<=c.n;b++)
{
if(juzhen[b][a]!=0)
{
num[b]++;
}
}
}
position[1]=1;
for(a=2;a<=len;a++)
{
position[a]=num[a-1]+position[a-1];
}
for(b=1;b<=c.len;b++)
{
int col=c.a[b].j;
int q=position[col];
y.a[q].i=c.a[b].j;
y.a[q].j=c.a[b].i;
y.a[q].x=c.a[b].x;
y.len++;
y.m=c.n;
y.n=c.m;
++position[col];
}
return y;
}整体性的代码如下所示,如果需要取走的朋友们请给个赞或者留个言谢谢
#include<iostream>
using namespace std;
int flag1=1;
int flag2=1;
int flag3=1;
class ju{
struct shu{
int i,j;
int x;
};
int m,n;
int len;
shu a[25];
public:
int juzhen[10][10];
ju(int o,int p);
void print()const;
void print1()const;
void generate();
void get_three();
int get_m()const;
int get_n()const;
ju Invert(ju y,ju c);
ju& add(ju c,ju &y);
ju& minus(ju c,ju &y);
ju& multi(ju c,ju &y);
};
void ju::get_three()
{
int i,j;
int k=1;
for(i=1;i<=m;i++)
{
for(j=1;j<=n;j++)
{
if(juzhen[i][j]!=0)
{
len++;
a[k].i=i;
a[k].j=j;
a[k].x=juzhen[i][j];
k++;
}
}
}
}
ju::ju(int o,int p) //初始化
{
m=o;
n=p;
len=0;
int j,i;
cout<<"请输入矩阵各个点的数字:\n";
for(i=1;i<=o;i++)
{
for(j=1;j<=p;j++)
{
cin>>juzhen[i][j];
}
}
}
int ju::get_m()const
{
return m;
}
int ju::get_n()const
{
return n;
}
ju & ju::add(ju c,ju &y)
{
int m1,n1;
m1=c.get_m();
n1=c.get_n();
if(m!=m1||n!=n1){
cout<<"您输入的矩阵格式不匹配\n";
flag1=0;
return *this;
}
for(int i=1;i<=m;i++)
{
for(int j=1;j<=n;j++)
{
y.juzhen[i][j]=juzhen[i][j]+c.juzhen[i][j];
}
}
return y;
}
ju & ju::minus(ju c,ju &y)
{
int m1,n1;
m1=c.get_m();
n1=c.get_n();
if(m!=m1||n!=n1){
cout<<"您输入的矩阵格式不匹配\n";
flag2=0;
return *this;
}
for(int i=1;i<=m;i++)
{
for(int j=1;j<=n;j++)
{
y.juzhen[i][j]=juzhen[i][j]-c.juzhen[i][j];
}
}
return y;
}
ju& ju::multi(ju c,ju &y)
{
if(n!=c.m){
cout<<"您输入的格式存在问题无法进行计算\n";
flag3=0;
}
for(int i=1;i<=m;i++)
{
for(int j=1;j<=c.n;j++)
{
for(int k=1;k<=c.m;k++)
y.juzhen[i][j]+=juzhen[i][k]*c.juzhen[k][j];
}
}
return y;
}
void ju::print()const //对矩阵和三元组进行打印
{
cout<<"矩阵结果如下:\n";
for(int i =1;i<=m;i++)
{
for(int j=1;j<=n;j++)
{
cout<<juzhen[i][j]<<" ";
}
cout<<endl;
}
cout<<endl;
cout<<"上述矩阵的三元组表示如下:\n";
for(int k=1;k<=len;k++)
{
cout<<a[k].i<<" "<<a[k].j<<" "<<a[k].x<<endl;
}
}
void ju::generate()
{
int k,i,j;
juzhen[10][10]={0};
for(k=1;k<=len;k++){
i=a[k].i;
j=a[k].j;
juzhen[i][j]=a[k].x;
}
}
ju ju::Invert(ju y,ju c)
{
int a,b;
int num[20],position[20];
for(a=1;a<=c.len;a++)
{
num[a]=0;
position[a]=0;
}
for(a=1;a<=c.m;a++)
{
for(b=1;b<=c.n;b++)
{
if(juzhen[b][a]!=0)
{
num[b]++;
}
}
}
position[1]=1;
for(a=2;a<=len;a++)
{
position[a]=num[a-1]+position[a-1];
}
for(b=1;b<=c.len;b++)
{
int col=c.a[b].j;
int q=position[col];
y.a[q].i=c.a[b].j;
y.a[q].j=c.a[b].i;
y.a[q].x=c.a[b].x;
y.len++;
y.m=c.n;
y.n=c.m;
++position[col];
}
return y;
}
int main()
{
int m1,n1,x,m2,n2;
char c;
cout<<"请输入第一个矩阵的格式:\n";
cin>>m1>>n1;
ju b(m1,n1);
b.get_three();
b.print();
cout<<"请输入第二个矩阵的格式:\n";
cin>>m2>>n2;
ju d(m2,n2);
d.get_three();
cout<<"是否要进行矩阵的运算:\n";
cin>>c;
while(c=='y'||c=='Y')
{
cout<<"运算如下:"
<<"1.矩阵加法add."
<<"2.矩阵减法minus."
<<"3.矩阵乘法."
<<"4.矩阵逆置."<<endl;
cout<<endl;
cout<<"请输入您要选择的运算:";
cin>>x;
if(x==1){
cout<<"请输入结果矩阵的各个元素必须定义为0\n";
ju y(m1,n1);
y=b.add(d,y);
if(flag1==0)
continue;
y.get_three();
cout<<"矩阵加法的结果为:\n";
y.print();
}
else if(x==2){
cout<<"请输入结果矩阵的各个元素必须定义为0\n";
ju a(m1,n1);
a=b.minus(d,a);
if(flag2==0)
continue;
a.get_three();
cout<<"矩阵减法的结果为:\n";
a.print();
}
else if(x==3){
cout<<"请输入结果矩阵的各个元素必须定义为0\n";
ju g(m1,n2);
g=b.multi(d,g);
if(flag3==0)
continue;
g.get_three();
cout<<"矩阵乘法的结果为:\n";
g.print();
}
else if(x==4){
ju h(m1,n1);
h=b.Invert(h,b);
h.generate();
h.print();
}
cout<<"是否要继续进行矩阵的运算:\n";
cin>>c;
}
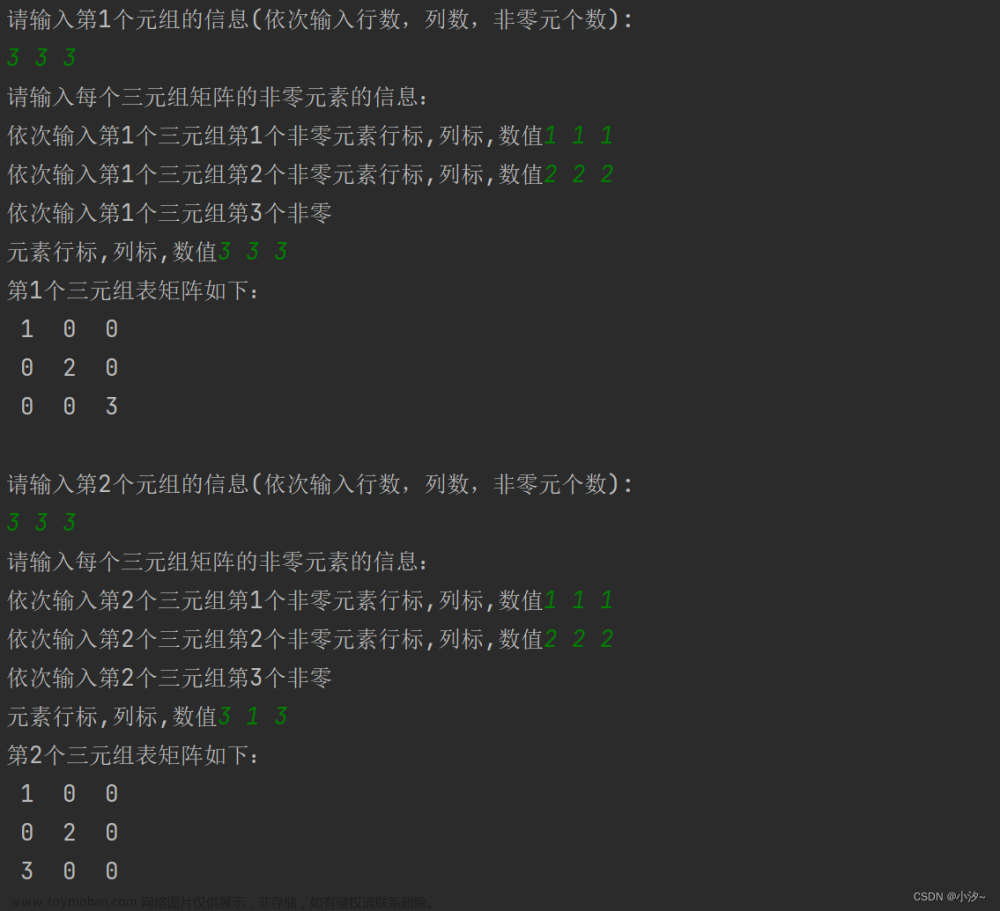
}运行的内容结果如下:




下面是一些测试错误的案例:
 文章来源:https://www.toymoban.com/news/detail-409271.html
文章来源:https://www.toymoban.com/news/detail-409271.html
本篇内容到此结束,有需要借走的朋友请留下点痕迹嘿嘿。文章来源地址https://www.toymoban.com/news/detail-409271.html
到了这里,关于C++数据结构稀疏矩阵运算(含加减乘及快速转置)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!