机器学习笔记之指数族分布——指数族分布介绍

引言

本节及后续小节将从指数族分布 $\to$ 熵、最大熵原理 $\to \text{sigmoid,softmax}$函数的思路进行介绍。

指数族分布介绍

指数族分布($\text{Exponential Families of Distributions}$)，它不是某一个分布，而是满足某种条件的分布集合。从名字可以看出，指数族分布描述的概率分布与指数相关。指数族分布的统一格式表示如下：
$$\mathcal{P}(x\mid \eta )=h(x)\exp \left\{{\eta }^T\varphi (x)-A(\eta )\right\}$$

如果只看公式等号左边 $\to P(x\mid \eta )$，在介绍极大似然估计与最大后验概率估计中介绍过，它可以表示为 基于参数向量$\eta$，生成随机样本$x$的概率模型。

我们称：

• $\varphi (x)$为充分统计量，它可以理解成样本的函数—— 如果已知充分统计量，就可以通过该统计量得到完整的概率分布表达形式。
  在后续的公式推导中进行证明。
• $\eta$表示生成概率模型$P(x\mid \eta )$的参数向量；
• $h(x)$仅表示关于$x$的一个函数，在一些具体分布中(如高斯分布、伯努利分布)通常以常数形式出现；
• $A(\eta )$通常表示为 $\log$配分函数(对数配分函数)($\text{log Partition Function}$)，在指数族分布主要起归一化作用，其本质是关于模型参数$\eta$的函数；
  因此，指数族分布还有另一种常见表达形式(将$A(\eta )$提出来)：
  P ( x ∣ η ) = h ( x ) exp ⁡ { η T ⋅ ϕ ( x ) } ⋅ exp ⁡ { − A ( η ) } = 1 exp ⁡ { A ( η ) } ⋅ h ( x ) exp ⁡ { η T ⋅ ϕ ( x ) } \begin{aligned} \mathcal P(x \mid \eta) & = h(x) \exp \left\{\eta^{T} \cdot \phi(x) \right\} \cdot \exp \{-A(\eta)\} \\ & = \frac{1}{\exp \{A(\eta)\}} \cdot h(x) \exp \left\{\eta^{T} \cdot \phi(x) \right\} \end{aligned} P(x∣η)​=h(x)exp{ηT⋅ϕ(x)}⋅exp{−A(η)}=exp{A(η)}1​⋅h(x)exp{ηT⋅ϕ(x)}​
  令 exp ⁡ { A ( η ) } = Z \exp \{A(\eta) \} = \mathcal Z exp{A(η)}=Z($\mathcal{Z}$表示 配分函数)；原始表示为：
  1 Z h ( x ) ⋅ exp ⁡ { η T ⋅ ϕ ( x ) } \frac{1}{\mathcal Z} h(x) \cdot \exp \{\eta^{T} \cdot \phi(x) \} Z1​h(x)⋅exp{ηT⋅ϕ(x)}
  因此，$A(\eta )=\log \mathcal{Z}$。 这也是$A(\eta )$对数配分函数的由来。
  配分函数相关:传送门

指数族分布应用广泛，如广义线性模型($\text{Generalized Linear Model,GLM}$)，概率图中的无向图模型如受限玻尔兹曼机($\text{Restricted Boltzmann Machine,RBM}$)均存在指数族分布的理论支撑；
甚至在深度强化学习中，使用策略梯度方法求解强化学习任务时，需要使用$\text{Softmax}$函数将离散型的动作映射成具有连续性质的指数族分布。

常见指数族分布

我们在概率论与数理统计中学习到的大部分分布都是指数族分布，下面列举一些常见分布：

• 高斯分布($\text{Normal Distribution}$)；
• 伯努利分布($\text{Bernoulli Distribution}$)；
• 二项分布($\text{Binomial Distribution}$)；
• 泊松分布($\text{Poisson Distribution}$)；
• 贝塔分布($\text{Beta Distribution}$)；
• 狄利克雷分布($\text{Dirichlet Distribution}$)；
• 伽马分布($\text{Gamma Distribution}$)等等。

下面对伯努利分布、高斯分布、二项分布进行推导，观察经过变化后的分布和指数族分布统一格式之间的关联关系。

推导过程

• 伯努利分布：
  $$\mathcal{P}(x)=p^x\cdot (1-p{)}^{1-x}=\{\begin{array}{l}p\text{if}x=1\\ q\text{if}x=0\end{array}$$

  将上述公式进行变化：

  • 插入$\exp$并完全展开：
    P ( x ) = p x ⋅ ( 1 − p ) 1 − x = exp ⁡ { log ⁡ [ p x ( 1 − p ) 1 − x ] } = exp ⁡ { x ⋅ log ⁡ [ p 1 − p ] + log ⁡ ( 1 − p ) } \begin{aligned} \mathcal P(x) & = p^x \cdot (1 - p)^{1-x} \\ & = \exp \{\log \left[p^x(1 - p)^{1-x} \right] \} \\ & = \exp \left\{x \cdot \log \left[\frac{p}{1- p}\right] + \log (1- p) \right\} \end{aligned} P(x)​=px⋅(1−p)1−x=exp{log[px(1−p)1−x]}=exp{x⋅log[1−pp​]+log(1−p)}​
  • 令$\begin{array}{r}\eta =\log \frac{p}{1-p}\end{array}$，那么$p$用$\eta$表示为：
    p = exp ⁡ { η } 1 + exp ⁡ { η } p = \frac{\exp \{\eta\}}{1 + \exp \{\eta \}} p=1+exp{η}exp{η}​
  • 将 $\begin{array}{r}p=\frac{e^{\eta }}{1+e^{\eta }}\end{array}$带回上述展开式：
    $$\begin{array}{rl}\mathcal{I}& =\exp \left\{x\cdot \eta +\log \left(1-\frac{e^{\eta }}{e^{\eta }+1}\right)\right\}\\ & =\exp \left\{x\cdot \eta +\log \left(\frac{1}{1+e^{\eta }}\right)\right\}\\ & =\exp \left\{{\eta }^{T}x-\log (1+e^{\eta })\right\}\end{array}$$

  观察变化后的公式，对照指数族分布的定义式，可以发现：

  • $\varphi (x)=x$
  • $h(x)=1$
  • $A(\eta )=\log (1+e^{\eta })$

  伯努利分布完全可以写成指数族分布的形式。

• 二项分布：
  二项分布可以看成$n$次独立重复的伯努利实验。它的概率分布表示如下：
  $$\mathcal{P}(x=k)={\mathcal{C}}_n^k{p}^k(1-p{)}^{n-k}$$
  其中，${\mathcal{C}}_n^k$表示二项式系数：
  $$C_n^k=\frac{n!}{k!(n-k)!}$$
  它的指数族分布表示和伯努利分布非常相似：

  • 插入$\exp$并完全展开：
    $$\begin{array}{rl}\mathcal{P}(x)& =\frac{n!}{x!(n-x)!}\cdot p^x(1-p{)}^{n-x}\\ & =\exp \left\{\log \left[\frac{n!}{x!(n-x)!}\cdot p^x(1-p{)}^{n-x}\right]\right\}\\ & =\exp \left\{\log \frac{n!}{x!(n-x)!}+x\log p+n\log (1-p)-x\log (1-p)\right\}\\ & =\exp \left\{\log \frac{n!}{x!(n-x)!}+x\log \frac{p}{1-p}+n\log (1-p)\right\}\end{array}$$
  • 由于$\begin{array}{r}\frac{n!}{x!(n-x)!}\end{array}$中$n$是表示实验次数，是常数，因此$\begin{array}{r}\frac{n!}{x!(n-x)!}\end{array}$可看做仅关于$x$的函数，将其提出；并令$\begin{array}{r}\eta =\log \frac{p}{1-p}\end{array}$，那么$\mathcal{P}(x)$用$\eta$表示为：
    $$p=\frac{e^{\eta }}{1+e^{\eta }}$$
  • 继续化简如下(将$p$带回原式)：
    $$\begin{array}{rl}\mathcal{I}& =\frac{n!}{x!(n-x)!}\exp \left\{x\log \frac{p}{1-p}+n\log (1-p)\right\}\\ & =\frac{n!}{x!(n-x)!}\exp \left\{{\eta }^{T}x-n\log (1+e^{\eta })\right\}\end{array}$$

  对照指数族分布定义式，获取参数如下：

  • $\varphi (x)=x$
  • $\begin{array}{r}h(x)=\frac{n!}{x!(n-x)!}\end{array}$
  • $A(\eta )=n\log (1+e^{\eta })$

• 一维高斯分布：
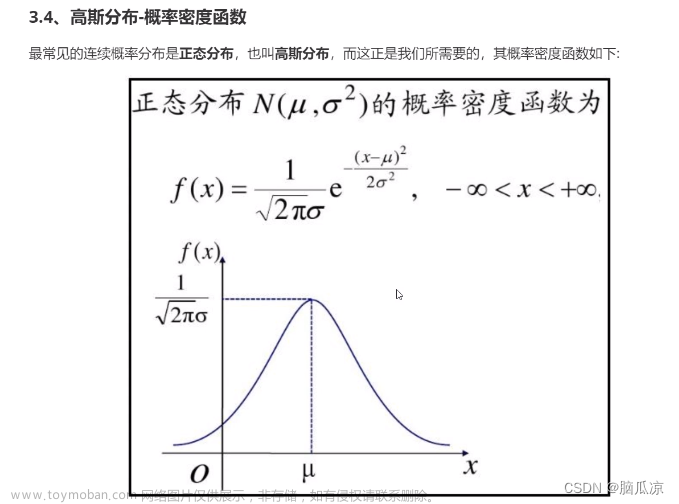
  $$\mathcal{P}(x\mid \theta )=\frac{1}{\sigma \sqrt{2\pi }}\cdot \exp \left\{-\frac{(x-\mu {)}^2}{2{\sigma }^2}\right\}$$
  同理，将上述公式完全展开，系数部分插入$\exp$：
  $$\begin{array}{rl}\mathcal{I}& =\exp \left\{\log {\left(2\pi {\sigma }^2\right)}^{-\frac{1}{2}}\right\}\cdot \exp \left\{-\frac{1}{2{\sigma }^2}\left(x^2-2\mu x+{\mu }^2\right)\right\}\\ & =\exp \left\{-\frac{1}{2}\log (2\pi {\sigma }^2)\right\}\cdot \exp \left\{-\frac{1}{2{\sigma }^2}(x^2-2\mu x)-\frac{{\mu }^2}{2{\sigma }^2}\right\}\end{array}$$
  此时，两项都有相同的底$\exp$，将两项合并；技巧操作：将$x^2-2\mu x$视为两向量的乘法操作。即：
  $$x^2-2\mu x=\left(\begin{array}{c}-2\mu ,1\end{array}\right)\left(\begin{array}{c}x\\ x^2\end{array}\right)$$
  化简得到如下结果：
  将$\begin{array}{r}-\frac{1}{2{\sigma }^2}\end{array}$作为系数带到矩阵中：
  $$-\frac{1}{2{\sigma }^2}\left(\begin{array}{c}-2\mu ,1\end{array}\right)=\left(\frac{\mu }{{\sigma }^2},-\frac{1}{2{\sigma }^2}\right)$$
  最终化简结果为：
  $$\exp \left\{\left(\frac{\mu }{{\sigma }^2},-\frac{1}{2{\sigma }^2}\right)\left(\begin{array}{c}x\\ x^2\end{array}\right)-\left[\frac{{\mu }^2}{2{\sigma }^2}+\frac{1}{2}\log (2\pi {\sigma }^2)\right]\right\}$$

  对照指数族分布定义式：

  • $\varphi =\left(\begin{array}{c}x\\ x^2\end{array}\right)$；
  • $h(x)=1$；
  • $\begin{array}{r}{\eta }^T=\left(\frac{\mu }{{\sigma }^2},-\frac{1}{2{\sigma }^2}\right)\end{array}$；
  • $\begin{array}{r}A(\eta )=\frac{{\mu }^2}{2{\sigma }^2}+\frac{1}{2}\log (2\pi {\sigma }^2)\end{array}$

实际上，我们可以对$\eta$继续化简：

• 令 η = ( η 1 η 2 ) = ( μ σ 2 − 1 2 σ 2 ) \eta = \begin{pmatrix}\eta_1\\\eta_2\end{pmatrix} = \begin{pmatrix} \begin{aligned}\frac{\mu}{\sigma^2}\end{aligned} \\ \begin{aligned}-\frac{1}{2\sigma^2}\end{aligned} \end{pmatrix} η=(η1​η2​​)= ​σ2μ​​−2σ21​​​ ​：
• 求得$\mu ,\sigma$表示如下：
  $$\mu =-\frac{{\eta }_1}{2\cdot {\eta }_2};{\sigma }^2=-\frac{1}{2\cdot {\eta }_2}$$
• $A(\eta )$表示为如下形式：
  $$A(\eta )=-\frac{{\eta }_1^2}{4{\eta }_2}+\frac{1}{2}\log \left(\frac{\pi }{{\eta }_2}\right)$$

回头观察充分统计量：
$$\varphi =\left(\begin{array}{c}x\\ x^2\end{array}\right)$$
如果某组数据 X = { x ( 1 ) , x ( 2 ) , ⋯   , x ( N ) } \mathcal X = \{x^{(1)},x^{(2)},\cdots,x^{(N)}\} X={x(1),x(2),⋯,x(N)}服从高斯分布，并且知晓该数据的两种信息：
( ∑ i = 1 N x ( i ) ∑ i = 1 N [ x ( i ) ] 2 ) \begin{pmatrix} \begin{aligned}\sum_{i=1}^N x^{(i)} \end{aligned} \\ \\ \begin{aligned} \sum_{i=1}^N [x^{(i)}]^2 \end{aligned} \end{pmatrix} ​i=1∑N​x(i)​i=1∑N​[x(i)]2​​ ​
那么该信息就可以构建一个完整的高斯分布模型$P(x\mid \eta )$， 并可以从该模型中源源不断地生成和$\mathcal{X}$相同分布的样本：
$$\{\begin{array}{l}\begin{array}{rl}\mu & =\frac{1}{N}\sum _{i=1}^N{x}_i\\ {\sigma }^2& =\sum _{i=1}^N{x}_i^2-{\mu }^2\end{array}\end{array}$$
有了均值$\mu$，方差$\sigma$，自然可以求解高斯分布：
$$\mathcal{P}(x\mid \theta )=\frac{1}{\sqrt{2\pi }\sigma }\exp \left\{-\frac{(x-\mu {)}^2}{2{\sigma }^2}\right\}$$
因此，指数族分布概率模型中的所有信息都存储在充分统计量中。换句话说，如果某一概率模型是指数族分布，那么该模型的统计量本身就是充分统计量。

指数族分布的共轭性质

在极大似然估计与最大后验概率估计介绍了贝叶斯估计及其弊端：
$$\mathcal{P}(\theta \mid x)=\frac{\mathcal{P}(x\mid \theta )\cdot \mathcal{P}(\theta )}{{\int }_{\theta }\mathcal{P}(x\mid \theta )\cdot \mathcal{P}(\theta )d\theta }$$

其本质是积分难问题，如果$\theta$是多维向量，每一维度都要计算积分，是相当耗费计算资源的事情。

共轭本身意思是指：给定特殊的似然$\mathcal{P}(x\mid \theta )$条件下，后验分布$\mathcal{P}(\theta \mid x)$与先验分布$\mathcal{P}(\theta )$会形成相同分布形式。
如果概率模型$\mathcal{P}(x\mid \theta )$是指数族分布，就可以满足共轭条件，在使用贝叶斯估计求解问题时，可以直接跳过求解分母积分的过程，这种性质为推断、模型选择提供很大便利。

具体表述逻辑如下：

• 如果概率模型(似然函数)$\mathcal{P}(x\mid \theta )$分布 存在一个共轭的先验分布$\mathcal{P}(\theta )$，那么效果是：后验分布$\mathcal{P}(\theta \mid x)$与先验分布$\mathcal{P}(\theta )$会形成相同分布形式。
  注意：先验分布和后验分布的分布形式相同，但并不是相等。

下一节将介绍指数族分布与最大熵的关系。

相关参考：
二项分布
指数族分布
机器学习-白板推导系列(八)-指数族分布（Exponential Family Distribution）文章来源地址https://www.toymoban.com/news/detail-409286.html

到了这里，关于机器学习笔记之指数族分布——指数族分布介绍的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！