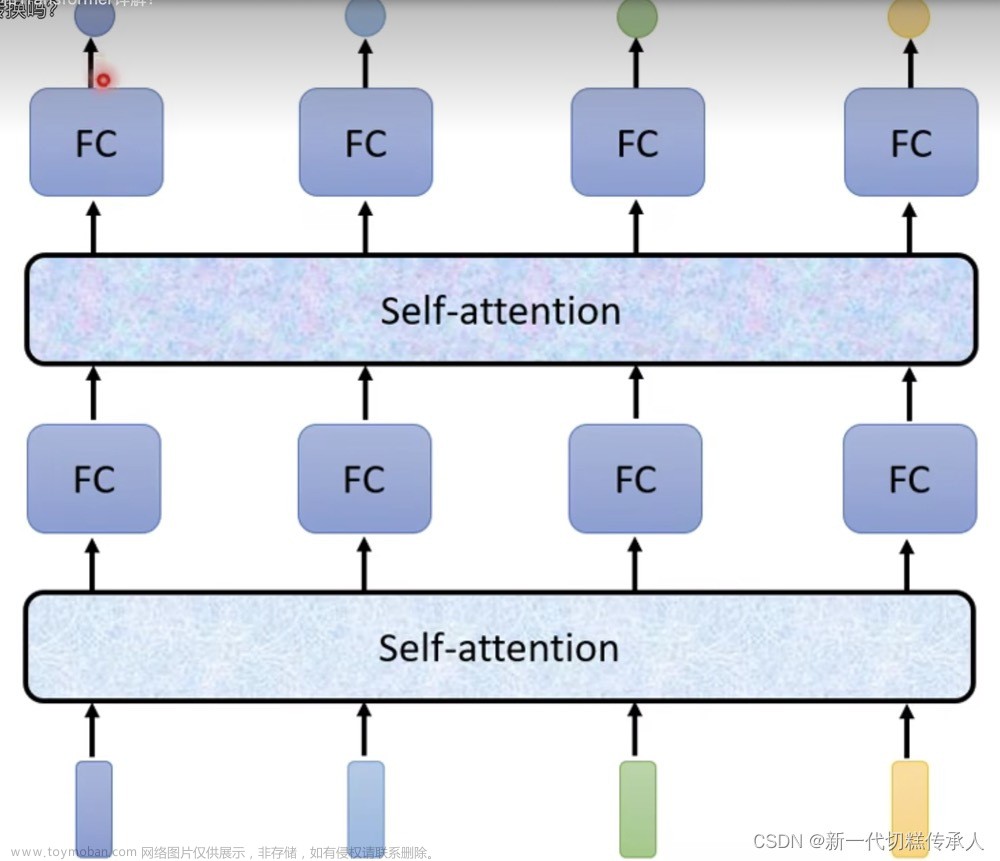
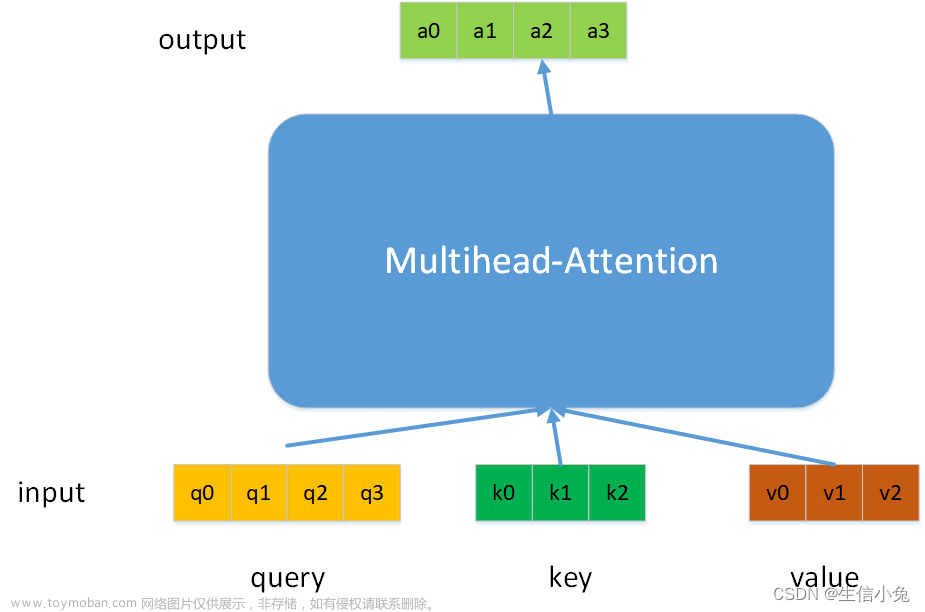
self-attention的公式为
a t t e n t i o n ( Q , K , V ) = S o f t m a x ( Q K d k ) V attention(Q,K,V)=Softmax( \frac{QK}{\sqrt{d_{k}}})V attention(Q,K,V)=Softmax(dkQK)V
个人理解,除以 d k \sqrt{d_{k}} dk的原因有两点:
d k d_{k} dk是词向量/隐藏层的维度
1、首先要除以一个数,防止输入softmax的值过大,导致偏导数趋近于0;
2、选择根号d_k是因为可以使得q*k的结果满足期望为0,方差为1的分布,类似于归一化。
公式分析,首先假设q和k都是服从期望为0,方差为1的独立的随机变量。
Assume: X = q i X=q_{i} X=qi, Y = k i Y=k_{i} Y=ki,那么:
1、 E ( X Y ) = E ( X ) E ( Y ) = 0 ∗ 0 = 0 E(XY)=E(X)E(Y)=0*0=0 E(XY)=E(X)E(Y)=0∗0=0
2、 D ( X Y ) = E ( X 2 Y 2 ) − [ E ( X Y ) ] 2 D(XY)=E(X^{2}Y^{2})-[E(XY)]^{2} D(XY)=E(X2Y2)−[E(XY)]2
= E ( X 2 ) E ( Y 2 ) − [ E ( X ) E ( Y ) ] 2 =E(X^{2})E(Y^{2})-[E(X)E(Y)]^{2} =E(X2)E(Y2)−[E(X)E(Y)]2
= E ( X 2 − 0 2 ) E ( Y 2 − 0 2 ) − [ E ( X ) E ( Y ) ] 2 =E(X^{2}-0^{2})E(Y^{2}-0^{2})-[E(X)E(Y)]^{2} =E(X2−02)E(Y2−02)−[E(X)E(Y)]2
= E ( X 2 − [ E ( X ) ] 2 ) E ( Y 2 − [ E ( Y ) ] 2 ) − [ E ( X ) E ( Y ) ] 2 =E(X^{2}-[E(X)]^{2})E(Y^{2}-[E(Y)]^{2})-[E(X)E(Y)]^{2} =E(X2−[E(X)]2)E(Y2−[E(Y)]2)−[E(X)E(Y)]2
= [ E ( X 2 ) − [ E ( X ) ] 2 ] [ E ( Y 2 ) − [ E ( Y ) ] 2 ] − [ E ( X ) E ( Y ) ] 2 =[E(X^{2})-[E(X)]^{2}][E(Y^{2})-[E(Y)]^{2}]-[E(X)E(Y)]^{2} =[E(X2)−[E(X)]2][E(Y2)−[E(Y)]2]−[E(X)E(Y)]2
= D ( X ) D ( Y ) − [ E ( X ) E ( Y ) ] 2 =D(X)D(Y)-[E(X)E(Y)]^{2} =D(X)D(Y)−[E(X)E(Y)]2
= 1 ∗ 1 − 0 ∗ 0 =1*1-0*0 =1∗1−0∗0
= 1 =1 =1
3、 D ( Q K d k ) = d k ( d k ) 2 = 1 D(\frac{QK}{\sqrt{d_{k}}})=\frac{d_{k}}{(\sqrt{d_{k}})^{2}}=1 D(dkQK)=(dk)2dk=1
需要注意的是, D ( Q K ) = D ( ∑ i = 0 d k q i k i ) = d k ∗ 1 = d k D(QK)=D(\sum_{i=0}^{d_{k}}q_{i}k_{i})=d_{k}*1=d_{k} D(QK)=D(∑i=0dkqiki)=dk∗1=dk文章来源:https://www.toymoban.com/news/detail-409357.html
附:AI工具箱
链接:https://hxmbzkv9u5i.feishu.cn/docx/Mv4Dd8TEYoUmTAxfpLtcUoOKnZc?from=from_copylink文章来源地址https://www.toymoban.com/news/detail-409357.html
到了这里,关于self-attention为什么要除以根号d_k的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!