算法分析与设计-数字三角形问题（动态规划）（通俗易懂，附源码和图解，含时间复杂度分析）（c++)-Toy模板网

这篇具有很好参考价值的文章主要介绍了算法分析与设计-数字三角形问题（动态规划）（通俗易懂，附源码和图解，含时间复杂度分析）（c++)。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

3-4数字三角形问题

（一）题目

问题描述

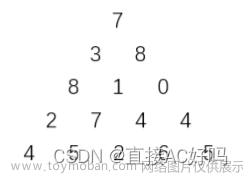
给定一个由 $n$ 行数字组成的数字三角形，如图所示。

        7
      3   8
    8   1   0
  2   7   4   4
4   5   2   6   5

试设计一个算法，计算从三角形的顶至底的一条路径，使该路径经过的数字总和最大。

算法设计

对于给定的由 $n$ 行数字组成的数字三角形，计算从该三角形的顶至底的路径经过的数字和的最大值。

数据输入

由文件input.txt提供输入数据。文件的第1行是数字三角形的行数 $n$ ， $1\leq n \leq 100$ 。接下来 $n$ 行是数字三角形各行中的数字，所有的数字在0~99之间。

结果输出

将计算结果输出到文件output.txt。文件的第1行中的数字是计算出的最大值。

（二）解答

方法思路

通过观察，我们可以看到：

数字三角形的最后一行上的数字到底的数字和最大的路径为该行上的数字本身；

数字三角形倒数第二行上的数字到底的数字和最大的路径为该行上的数字加上该行左下或右下的数字之和；

…

以此类推，我们可以从下往上推出数字三角形的顶至底的路径经过的数字和的最大值。

设该问题的子问题——从数字三角形中的第 $i$ 行，第 $j$ 列的数字出发至低端所经过的路径上的数字和的最大值为 $t r i a n g l e (i, j)$ ，由最优子结构性质，可以建立计算 $t r i a n g l e (i, j)$ 的递归式如下:
$triangle(i,j)=\begin{cases} triangle(i,j),\;\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \qquad \qquad \quad \qquad i=n\\ triangle(i,j)+max\{triangle(i+1,j),triangle(i+1,j+1)\},\qquad 1\leq i<n\\ \end{cases}$
按此递归式计算出的 $t r i a n g l e (1, 1)$ 即为所求。

举例

算法分析与设计-数字三角形问题（动态规划）（通俗易懂，附源码和图解，含时间复杂度分析）（c++)

源代码

#include<iostream>
#include<cstdio>
#include<fstream>

using namespace std;

int n; //数字三角形行数
int triangle[101][1001]; //数字三角形数组
int s[101]; //路径数组

//读取
void Read(); 
//写入
void Write();
//求解从三角形顶端到底端的路径所经过的数字和的最大值
void Solution(int n, int triangle[][1001]);
//求解路径数组
void TrackBack(int n, int triangle[][1001]);

int main()
{
    //读取
    Read();
    //求解从三角形顶端到底端的路径所经过的数字和的最大值
    Solution(n, triangle);
    //写入
    Write();
    //输出最优解路径
    TrackBack(n, triangle);
    for (int i = 1; i <= n; ++i)
    {
        cout<<s[i]<<" ";
    }
    cout<<endl;
    return 0;
}

void Read()
{
    ifstream ifs;
    //打开输入文件
    ifs.open("G:\\algorithm\\data\\3_4_input.txt", ios::in);
    //读取数据
    ifs>>n;
    for (int i = 1; i <= n; ++i)
    {
        for (int j = 1; j <= i; ++j)
        {
            ifs>>triangle[i][j];
        }
    }
    //关闭输入文件
    ifs.close();
}

void Write()
{
    ofstream ofs;
    //创建输出文件
    ofs.open("G:\\algorithm\\data\\3_4_output.txt", ios::out);
    //写入数据
    ofs<<triangle[1][1]<<endl;
    //关闭输出文件
    ofs.close();
}

void Solution(int n, int triangle[][1001])
{
    //从下往上计算
    for (int i = n - 1; i >= 1; --i)
    {
        for (int j = 1; j <= i; ++j)
        {
            triangle[i][j] += max(triangle[i + 1][j], triangle[i + 1][j + 1]);
        }
    }
}

void TrackBack(int n, int triangle[][1001])
{
    //从上往下计算
    int i, j, maxium;
    i = j = 1;
    while(i < n)
    {
        if (triangle[i + 1][j] > triangle[i + 1][j + 1])
        {
            s[i] = triangle[i][j] - triangle[i + 1][j];
            i = i + 1;
            j = j;
        }
        else
        {
            s[i] = triangle[i][j] - triangle[i + 1][j + 1];
            i = i + 1;
            j = j + 1;
        }
    }
    s[i] = triangle[i][j];
}