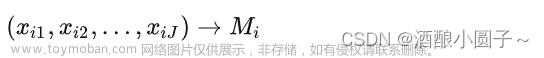最近在学习数学建模，在B站发现一个特别不错的课程，讲的很全面，常考的算法都有涉及到：清风数学建模
本文将结合熵权法介绍TOPSIS法，并将淡化原理的推导，更侧重于具体应用。
TOPSIS法
概述
TOPSIS法（优劣解距离法）是一种常用的综合评价方法，能充分利用原始数据的信息，其结果能精确地反映各评价方案之间的差距。同时TOPSIS法也可以结合熵权法使用确定各指标所占的权重。
基本过程
一、统一指标类型
常见的四种指标如下：
在进行建模之前需要对所有的指标进行正向化处理，正向化的过程就是将所有指标类型统一转化为极大型指标（越大越好）的过程（转换函数形式不唯一）。假设原始数据序列为x，则各类型指标转化为极大型指标的方法如下：
- 极小型指标→极大型指标：
max - x - 中间型指标→极大型指标：
假设最佳数值为xbest，X为正向化后的序列，则正向化公式为：
M = max{|xi-xbest|}，X = 1 - |xi-xbest|/M - 区间型指标→极大型指标：
假设最佳区间为[a,b]，则正向化公式如下：
M = max{a - min{x},max{x}-b}
二、正向化矩阵标准化
标准化的目的是消除不同指标量纲的影响。
设正向化矩阵为X，则标准化矩阵Z为：
除上述方法以外，还有许多方法，如：(x - x的均值) / x的标准差，具体选用哪一种方法在多数情况下并没有很大限制。
三、计算得分并归一化
假设有n个要评价的对象，m个评价指标的大小为 n×m 标准化矩阵Z。
定义最大值：
定义最小值：
定义第 i 个评价对象与最大值的距离：
定义第 i 个评价对象与最小值的距离：
可以计算第 i 个评价对象未归一化的得分：
将得分归一化（得分归一化不影响排序）：
以上分析过程未考虑指标的权重，可以使用熵权法来确定各指标的权重。
综上所述，算法基本过程如下：
- 将原始数据矩阵进行正向化处理， 得到正向化矩阵；
- 对正向化矩阵进行标准化处理以消除各指标量纲的影响，并找出有限方案中的最优方案与最劣方案；
- 分别计算各评价对象与最优方案和最劣方案之间的距离；
- 根据“构造计算评分公式”获得各评价对象与最优方案的接近程度，作为评价优劣的依据。
基于熵权法对Topsis法模型的修正
基本原理
熵权法是一种客观赋权的方法，依据的原理为：指标的变异程度越小，所反映的信息量也越少，其对应的权值也越低（客观等同于数据本身就可以告诉我们权重）。
熵权法的性质：越有可能发生的事情，信息量越少；越不可能发生的事情，信息量就越多。信息量与概率的函数关系如下：
设 x 为事件X发生的某种情况，p(x) 表示这种情况发生的概率，则 I(x) = -ln(p(x))。
定义事件 X 的信息熵为：
即，信息熵的本质是对信息量的期望值。对于熵权法而言，因为关注的是已有的信息，所以信息熵越大，信息量越小（随机变量的信息熵越大，则它的值（内容）能为你补充的信息量越大，而在知道这个值之前你已有的信息量越小）。
熵权法的计算步骤
- 判断矩阵中是否存在负数，如果有则要重新标准化到非负区间（后续步骤计算概率时要保证每一个元素为非负数）：
假设有 n 个要评价的对象，m 个评价指标（已经经过正向化），构成正向化矩阵 X，则其标准化的矩阵Z中每一个元素满足：
如果矩阵 Z 中存在负数，则要对 X 使用另一种标准化方法：
-
计算第 j 项指标下第 i 个样本所占的权重，并将其看作相对熵计算中用到的概率：
对于上一步得到的非负标准化矩阵，计算其概率矩阵P，且P中每一个元素的计算公式如下：
-
计算每一个指标的信息熵，并计算信息效用值，并归一化得到的每个指标的熵权
对于第 j 个指标而言，其信息熵的计算公式为：
信息效用值的定义：
将信息效用值进行归一化，就能得到每个指标的熵权：
考虑权重的TOPSIS法
上述介绍的TOPSIS法未考虑各指标的权重，当使用熵权法计算出各指标的权重时，仅需要重新计算各评价对象的D+与D-即可，其它步骤与上述未考虑权重的步骤相同。
定义第 i 个评价对象与最大值的距离：
定义第 i 个评价对象与最小值的距离：
文章来源：https://www.toymoban.com/news/detail-409975.html
由于最近比较忙的原因，所以本文可能存在不完善的地方，后续会继续完善文章。文章来源地址https://www.toymoban.com/news/detail-409975.html
到了这里，关于基于熵权法对TOPSIS法模型的修正的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
