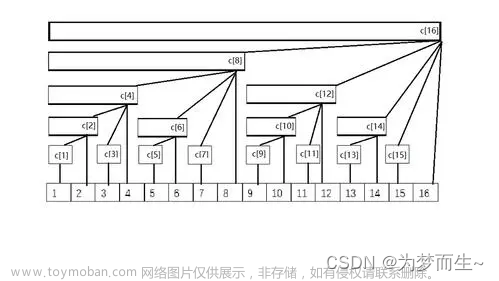
0x42 树状数组
楼兰图腾
题意:
二维平面给定一些点,询问 v 形和 ∧ 形数目
解析:
对于 ∧ 形: ( i , y ) (i,y) (i,y),考虑左右两侧比该点低的点的个数。树状数组查询 y j < y y_j< y yj<y 的点的个数。因为总共有 y − 1 y-1 y−1 个点比当前点低,有 n − y n-y n−y 个点比当前点高。
v型同理。
代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef double db;
#define fi first
#define se second
const int maxn = 4e5+10;
const int N = 4E5;
const int INF = 0x3f3f3f3f;
typedef pair<int, int> pii;
ll c[maxn];
int lowbit(int x){
return x & (-x);
}
void add(int x, int v){
for(; x <= N; x += lowbit(x))
c[x] += v;
}
ll query(int x){
ll res = 0;
while(x){
res += c[x];
x -= lowbit(x);
}
return res;
}
ll lsmall[maxn], lbig[maxn], rsmall[maxn], rbig[maxn], y;
int n;
int main(){
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
//BIT tr;
cin >> n;
for(int i = 1; i <= n; i++){
cin >> y;
lsmall[i] = query(y-1);
rsmall[i] = y-1-lsmall[i];
lbig[i] = i-1-lsmall[i];
rbig[i] = n-y-lbig[i];
add(y, 1);
}
ll ans1 = 0, ans2 = 0;
for(int i = 1; i <= n; i++){
ans1 += lbig[i] * rbig[i];
ans2 += lsmall[i] * rsmall[i];
}
cout << ans1 << " " << ans2 << endl;
return 0;
}
一个简单的整数问题
题意:
区间加,单点查询。
解析:
树状数组维护差分数组。
区间加为单点修改,单点查询为查询差分数组的前缀和。
代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef double db;
#define fi first
#define se second
const int maxn = 1e5+10;
const int INF = 0x3f3f3f3f;
typedef pair<int, int> pii;
int n, m, a[maxn];
int ls(int x){return x << 1;}
int rs(int x){return x << 1 | 1;}
struct sgt{
int lmax, rmax, maxx, sum;
sgt(){
lmax = rmax = maxx = -INF;
sum = 0;
}
}t[maxn << 2];
void pushup(int k){
t[k].sum = t[ls(k)].sum + t[rs(k)].sum;
t[k].lmax = max(t[ls(k)].lmax, t[ls(k)].sum + t[rs(k)].lmax);
t[k].rmax = max(t[rs(k)].rmax, t[rs(k)].sum + t[ls(k)].rmax);
t[k].maxx = max(t[ls(k)].maxx, t[rs(k)].maxx);
t[k].maxx = max(t[k].maxx, t[ls(k)].rmax+t[rs(k)].lmax);
}
void pushup(sgt &k, sgt lson, sgt rson){
k.sum = lson.sum + rson.sum;
k.lmax = max(lson.lmax, lson.sum + rson.lmax);
k.rmax = max(rson.rmax, rson.sum + lson.rmax);
k.maxx = max(lson.maxx, rson.maxx);
k.maxx = max(k.maxx, lson.rmax+rson.lmax);
}
void build(int k, int l, int r){
if(l == r){
t[k].lmax = t[k].rmax = t[k].maxx = t[k].sum = a[l];
return;
}
int mid = (l+r) >> 1;
build(ls(k), l, mid);
build(rs(k), mid+1, r);
pushup(k);
}
void modify(int k, int l, int r, int pos, int w){
if(l == r && l == pos){
t[k].lmax = t[k].rmax = t[k].maxx = t[k].sum = w;
return;
}
int mid = (l+r) >> 1;
if(pos <= mid)
modify(ls(k), l, mid, pos, w);
else
modify(rs(k), mid+1, r, pos, w);
pushup(k);
}
sgt query(int k, int l, int r, int x, int y){
if(x <= l && y >= r)
return t[k];
int mid = (l+r) >> 1;
sgt lres, rres, res;
if(x <= mid)
lres = query(ls(k), l, mid, x, y);
if(y > mid)
rres = query(rs(k), mid+1, r, x, y);
pushup(res, lres, rres);
return res;
}
int main(){
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cin >> n >> m;
for(int i = 1; i <= n; i++)
cin >> a[i];
build(1, 1, n);
int op, x, y;
while(m--){
cin >> op >> x >> y;
if(op == 1){
if(x > y)
swap(x, y);
cout << query(1, 1, n, x, y).maxx << endl;
}
else if(op == 2){
modify(1, 1, n, x, y);
}
}
return 0;
}
一个简单的整数问题2
题意:
区间加,区间查询
解析:
区间加,需要用树状数组维护差分数组。区间查询,需要求出原数组的前缀和数组。
设原数组为 a a a,差分数组为 d d d,前缀和数组为 s u m sum sum
s u m n = ∑ i = 1 n a i = ∑ i = 1 n ( ∑ j = 1 i d j ) = ( n + 1 ) ∑ i = 1 n d i − ∑ i = 1 n i ⋅ d i sum_n = \sum\limits_{i=1}\limits^na_i = \sum\limits_{i=1}\limits^n(\sum\limits_{j=1} \limits^id_j)=(n+1)\sum\limits_{i=1}\limits^nd_i-\sum\limits_{i=1}\limits^ni\cdot d_i sumn=i=1∑nai=i=1∑n(j=1∑idj)=(n+1)i=1∑ndi−i=1∑ni⋅di
所以需要两个树状数组,维护 d d d 和 i ⋅ d i i\cdot d_i i⋅di
树状数组代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef double db;
#define fi first
#define se second
const int maxn = 4e5+10;
const int N = 4E5+10;
const int INF = 0x3f3f3f3f;
typedef pair<int, int> pii;
int lowbit(int x){return x & (-x);}
struct BIT{
ll c[maxn];
void add(int x, ll v){
for(; x <= N; x += lowbit(x))
c[x] += v;
}
void update(int l, int r, int d){
add(l, d);
add(r+1, -d);
}
ll query(int x){
ll res = 0;
while(x){
res += c[x];
x -= lowbit(x);
}
return res;
}
}tr1, tr2;
ll sum(int x){
return tr1.query(x) * (x+1) - tr2.query(x);
}
ll n, m, a[maxn];
signed main(){
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cin >> n >> m;
for(int i = 1; i <= n; i++){
cin >> a[i];
tr1.update(i, i, a[i]);
tr2.add(i, i*a[i]); tr2.add(i+1, -(i+1)*a[i]);
}
string op;
ll l, r, d;
while(m--){
cin >> op;
if(op == "C"){
cin >> l >> r >> d;
tr1.update(l, r, d);
tr2.add(l, l*d); tr2.add(r+1, -(r+1)*d);
}
else if(op == "Q"){
cin >> l >> r;
cout << sum(r)-sum(l-1) << endl;
}
}
return 0;
}
线段树代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef double db;
#define fi first
#define se second
const int maxn = 1e5+10;
const int INF = 0x3f3f3f3f;
typedef pair<int, int> pii;
int a[maxn], n, m;
int ls(int x){return x << 1;}
int rs(int x){return x << 1 | 1;}
struct sgt{
ll v, tag;
}t[maxn << 2];
void pushup(int k){
t[k].v = t[ls(k)].v + t[rs(k)].v;
}
void build(int k, int l, int r){
t[k].tag = 0;
if(l == r){
t[k].v = a[l];
return;
}
int mid = (l+r) >> 1;
build(ls(k), l, mid);
build(rs(k), mid+1, r);
pushup(k);
}
void pushdown(int k, int l, int r){
if(t[k].tag){
int mid = (l+r) >> 1;
t[ls(k)].v += (mid-l+1) * t[k].tag;
t[ls(k)].tag += t[k].tag;
t[rs(k)].v += (r-mid) * t[k].tag;
t[rs(k)].tag += t[k].tag;
t[k].tag = 0;
}
}
void modify(int k, int l, int r, int x, int y, ll w){
if(x <= l && y >= r){
t[k].tag += w;
t[k].v += (r-l+1) * w;
return;
}
int mid = (l+r) >> 1;
pushdown(k, l, r);
if(x <= mid)
modify(ls(k), l, mid, x, y, w);
if(y > mid)
modify(rs(k), mid+1, r, x, y, w);
pushup(k);
}
ll query(int k, int l, int r, int x, int y){
if(x <= l && y >= r)
return t[k].v;
pushdown(k, l, r);
int mid = (l+r) >> 1;
ll res = 0;
if(x <= mid)
res += query(ls(k), l, mid, x, y);
if(y > mid)
res += query(rs(k), mid+1, r, x, y);
return res;
}
int main(){
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cin >> n >> m;
for(int i = 1; i <= n; i++)
cin >> a[i];
build(1, 1, n);
string op;
int l, r, d;
while(m--){
cin >> op;
if(op == "C"){
cin >> l >> r >> d;
modify(1, 1, n, l, r, d);
}
else if(op == "Q"){
cin >> l >> r;
cout << query(1, 1, n, l, r) << endl;
}
}
return 0;
}
谜一样的牛
题意:
n n n 头牛,身高为1-n的排列。第 i i i 头牛前有 A i A_i Ai 头牛比该牛矮,询问每头牛的身高。
解析:
只有最后一头牛的身高能直接确定,假设 A n = x A_n = x An=x,则 h n = x + 1 h_n = x+1 hn=x+1。倒数第二头牛的身高也能确定了,设 A n − 1 = y A_{n-1} = y An−1=y,则 身高为身高可用集合中第 y + 1 y+1 y+1 小的。
设 a i a_i ai 表示身高 i i i 是否可用, a i = 1 a_i = 1 ai=1 表示可用。 a a a 的前缀和具有单调性,可以二分。
需要支持区间查询和单点修改。所以用树状数组维护 a a a文章来源:https://www.toymoban.com/news/detail-410118.html
时间复杂度为 O ( n l o g 2 n ) O(nlog^2n) O(nlog2n)文章来源地址https://www.toymoban.com/news/detail-410118.html
代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef double db;
#define fi first
#define se second
const int maxn = 2e5+10;
const int N = 2e5;
const int INF = 0x3f3f3f3f;
typedef pair<int, int> pii;
ll c[maxn];
int lowbit(int x){
return x & (-x);
}
void add(int x, int v){
for(; x <= N; x += lowbit(x))
c[x] += v;
}
ll query(int x){
ll res = 0;
while(x){
res += c[x];
x -= lowbit(x);
}
return res;
}
ll sum(int l, int r){
return query(r) - query(l-1);
}
int n, m, a[maxn], h[maxn];
int main(){
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cin >> n;
for(int i = 2; i <= n; i++)
cin >> a[i];
for(int i = 1; i <= n; i++)
add(i, 1);
for(int i = n; i >= 1; i--){
int l = 1, r = n, pos;
while(l <= r){
int mid = (l+r) >> 1;
if(sum(1, mid) >= a[i]+1){
r = mid-1;
pos = mid;
}
else
l = mid+1;
}
h[i] = pos;
add(pos, -1);
}
for(int i = 1; i <= n; i++)
cout << h[i] << endl;
return 0;
}
到了这里,关于《算法竞赛进阶指南》0x42 树状数组的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!


![【算法每日一练]-结构优化(保姆级教程 篇4 树状数组,线段树,分块模板篇)](https://imgs.yssmx.com/Uploads/2024/02/759135-1.jpeg)







