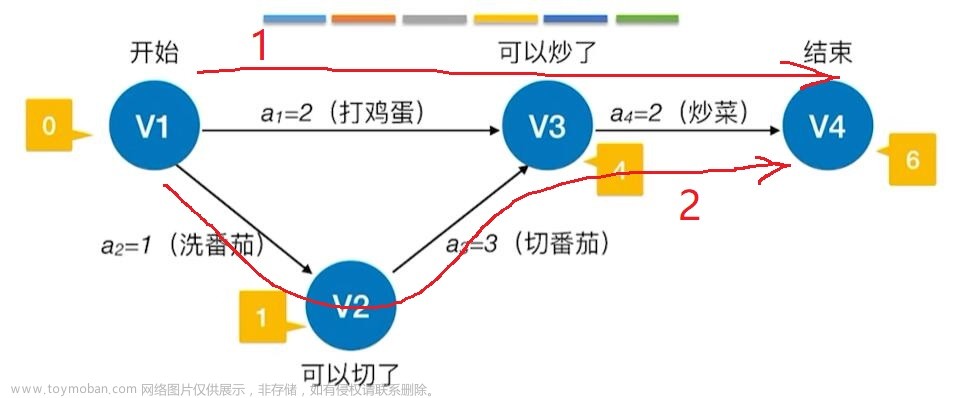
关键路径法是在进度模型中,估算项目最短工期,确定逻辑网络路径进度灵活性大小的一种方法。
①计算原理
a.计算ES、EF:从网络计划起点节点开始,沿箭线方向依次向前推算,数值取大。
b.计算LS、LF:从网络计划终点节点开始,逆箭线方向依次向前推算,数值取小。
②计算步骤:D→①ES→②EF→③Tp→④LF→⑤LS→⑥TF→⑦FF (D为持续时间)
③关键工作与关键线路的判定:总时差最小的工作是关键工作。
当Tc=Tp时:a.TF=0的工作是关键工作;
b.LF-EF=0的工作是关键工作;
c.LS-ES=0的工作是关键工作。
注意点:
关键路径是项目网络图中总工期最长的路径,决定了项目所需的最短时间;
关键路径至少有一条,且可以有多条;
关键路径上的计划活动叫做“关键活动”,关键活动的时差通常为零或负;
找关键路径没有捷径,只有每一条都去计算一遍。
相关公式
最早开始时间(ES) |
工期/持续时间(DU) |
最早完成时间(EF) |
工作名称 | ||
最晚开始时间(LS) |
总时差(TF) |
最晚完成时间(LF) |
EF =ES +DU(默认ES从0开始)
LF = LS +DU(默认ES从0开始)
总时差=最晚开始时间-最早开始时间=最晚完成时间-最早完成时间
总时差可能为正、负或零。关键路径有零或者负值的总时差
自由时差=后继活动最早开始时间-本活动最早完成时间
网络图中关键线路、关键工作的判定:
①双代号网络计划。
总时差最小的工作为关键工作,自始至终由关键工作组成的路段为关键线路。当Tp=Tc时,总时差为0的工作即为关键工作。
②单代号网络计划:
a.将关键工作相连,并保证相邻两项关键工作之间的时间间隔为零而构成的线路就是关键线路。
b.从网络计划的终点节点开始,逆着箭线的方向依次找出相邻两项工作之间的时间间隔为零的线路就是关键线路。
③双代号时标网络计划。自终至始都不出现波形线的线路即为关键线路
CPM 分析:





示例
已知某信息工程由 A、B、C、D、E、F、G、H 八个活动构成,项目的活动历时,活动所需
人数、费用及活动逻辑关系如下表所示:
活动 |
历时(单位:天) |
紧前活动 |
A |
3 |
- |
B |
2 |
A |
C |
8 |
A |
D |
4 |
B |
E |
10 |
C |
F |
7 |
C |
G |
8 |
D |
H |
5 |
E,F,G |
【问题 1】 画出网络图,计算每个活动的ES、LS、EF、LF、总时差和自由时差

【问题 2】 计算关键路径
关键路径是 ACEH,工期是 26 天
例题:1、某工程双代号网络计划如下图所示,其中关键线路有( )条。

A.2 B.3 C.4 D.5
【答案】B 解析:本题考查的是关键线路的判断。关键线路有三条,分别为:①→④→⑥→⑧;①→②→⑦→⑧;①→②→③→⑤→⑥→⑧。工期为20。
2、计划工期与计算工期相等的双代号网络计划中,某工作的开始节点和完成节点均为关键节点时,说明该工作( )。
A.—定是关键工作
B.总时差为零
C.总时差等于自由时差
D.自由时差为零
【答案】C 解析:本题考查的是网络计划时间参数的计算。对于网络计划中以关键节点为完成节点的工作,其自由时差与总时差相等。
3、在工程网络计划中,关键工作是指( )的工作。
A.最迟完成时间与最早完成时间之差最小
B.自由时差为零
C.总时差最小
D.持续时间最长
E.时标网络计划中没有波形线
【答案】AC 解析:关键工作的概念。选项B错误,自由时差为0,不一定为关键工作;选项D错误,持续时间最长的工作,不一定为关键工作;相反持续时间最长的线路,一定是关键线路;选项E错误,时标网络计划中没有波形线,不一定为关键工作。
4、某工程网络计划中,工作M有两项紧后工作,最早开始时间分别为12和13。工作M的最早开始时间为8,持续时间为3,则工作M的自由时差为( )。
A.1 B.2 C.3 D.4
【答案】A 解析:工作M的最早结束时间为8+3=11,由于最早开始时间分别为12和13,13-11=2,12-11=1,所以M工作的自由时差取最小值,即M的自由时差为1。
三点估算(PERT)
1.公式
预期值 =(乐观值*4+最可能值+悲观值)/6
2.正态分布
均值=预期值=(乐观值+最可能值*4+悲观值)/6
标准差 =(悲观时间-乐观时间)/6
3.牢记下图:
一个标准差:68.26%
两个标准差:95.46%
三个标准差:99.73%

4.示例
完成活动A所需要的时间,悲观估计需要36天,最可能的估计是21天,乐观估计需要6天。活动A在16天和26天内完成的概率是多少?
解答:期望时间=(乐观值*4+最可能值+悲观值)/6=(36+6+21*4)=21天;
标准差=(悲观时间-乐观时间)/6 =(36-6)/6=5天
一个正负标准差的范围是16天(21-5)到26天(21+5)天,查看整体分布图可知,概率为68.26%
总时差和自由时差
1、看到总时差,一定使用的是关键路线法,因为关键路线是通过总时差的计算找到的。
2、是总时差决定了进度表的灵活余地,而自由时差只影响紧后活动。
3、网络路线、活动都可以有总时差,而自由时差只有活动才有。
4、不受其他路线影响之前,同一条路线的总时差是传导的,即活动的总时差都相等、路线总时差也等于各活动的总时差,总时差不能相加。
5、总时差的计算是同一活动的最晚(开始或结束)减最早(开始或结束),正的就是正的,负的就是负的;比较总时差大小时,不考虑绝对值,正总时差大于负的总时差。
6、如果只说时差,那就是总时差。
时差的利用
①如果延期的工作位于关键线路上,不管延期多长时间,对总工期和后续工作都有影响;
②如果延期的工作不在关键线路上,对总工期和后续工作是否有影响,取决于延期的时间与总时差和自由时差的关系:
A.延期时间>总时差,对总工期和后续工作都有影响。
B.总时差≥延期时间>自由时差,对总工期没有影响,对后续工作有影响。
C.延期时间≤自由时差,对总工期和后续工作都没有影响。
1·公式
总时差=最晚开始-最早开始=最晚结束-最早结束
自由时差=后一个活动的最早开始-前一个活动的最早结束
借用这幅图为例:

2·总时差
B活动的总时差套用公式是3-2=1:

总时差是由图的终结活动“E”向前推算而来。故表示对最后一个活动的影响,即对于整个项目的影响。
3·自由时差
B活动的自由时差套用公式是5-5=0:

自由时差是由前后活动推算而来,体现的是前后活动间的关系。故体现前一个活动对于后一个活动的影响。
【例题1·单选】关于关键工作和关键线路的说法正确的是( )。
A.关键线路上的工作全部是关键工作
B.关键工作不能在非关键线路上
C.关键线路上不允许出现虚工作
D.关键线路上的工作总时差均为零
【答案】A 【解析】非关键路线上也可能有关键工作,所以B错误;关键线路上允许有虚工作,故C错误;少了前提条件“计划工期=计算工期时”,所以D错误。
【例题2·单选】某双代号网络计划中,工作M的自由时差3天,总时差5天。在进度计划实施检查中发现工作M实际进度落后,且影响总工期2天。在其他工作均正常的前提下,工作M的实际进度落后( )天。【2016】
A. 7 B. 5 C. 6 D. 8
【答案】A 【解析】本题考查总时差与自由时差的相关概念。由题意可知,M工作总时差5天,且M实际进度落后,影响总工期2天,因此M实际工作了5+2=7天。
【例题3·多选】当计算工期超过计划工期时,可压缩关键工作的持续时间以满足要求,在确定缩短持续时间的关键工作时,宜选择( )。
A.有多项紧前工作的工作
B.缩短持续时间而不影响质量和安全的工作
C.有充足备用资源的工作
D.缩短持续时间所增加的费用相对较少的工作
E.单位时间消耗资源量大的工作
【答案】BCD 【解析】当计算工期不能满足计划工期时,可设法通过压缩关键工作的持续时间,以满足计划工期要求。在选择缩短持续时间的关键工作时,宜考虑下述因素:
(1)缩短持续时间而不影响质量和安全的工作;
(2)有充足备用资源的工作;
(3)缩短持续时间所需增加的费用相对较少的工作等。
【例题4·单选】在双代号网络计划中,如果其计划工期等于计算工期,且工作i -j的完成节点j在关键线路上,则工作i-j的自由时差( )。
A.等于零 B.小于零 C.小于其相应的总时差 D.等于其相应的总时差
答案:D 解析:本题主要考察自由时差和总时差的概念。由于工作i-j的完成节点j在关键线路上,说明节点j为关键节点,即工作i -j的紧后工作中必有关键工作,此时工作i-j的自由时差就等于其总时差。
【例题5·单选】在某工程双代号网络计划中,工作M的最早开始时间为第15天,其持续时间为7 天。该工作有两项紧后工作,它们的最早开始时间分别为第27天和第30 天,最迟开始时间分别为第28天和第33 天,则工作M的总时差和自由时差( )天。
A.均为5 B.分别为6和5 C.均为6 D.分别为11 和6
答案:B 解析:本题主要是考六时法计算方法
1、工作M的最迟完成时间=其紧后工作最迟开始时间的最小值所以工作M的最迟完成时间等于[28,33]=28
2、工作M的总时差 = 工作M的最迟完成时间 - 工作M的最早完成时间等于28-(15+7)=6
3、工作M的自由时差 = 工作M的紧后工作最早开始时间减工作M的最早完成时间所得之差的最小值:[27-22; 30-22]= 5。
【例题6·单选】在工程网络计划中,判别关键工作的条件是该工作( )。
A.结束与紧后工作开始之间的时距最小 B.与其紧前工作之间的时间间隔为零
C.与其紧后工作之间的时间间隔为零 D.最迟开始时间与最早开始时间的差值最小
答案:D 解析:因为总时差最小的工作为关键工作,这是总时差的概念,而最迟开始时间与最早开始时间的差值就是总时差,所应选D。
【例题7·单选】当工程网络计划的计算工期小于计划工期时,则( )。
A.单代号网络计划中关键线路上相邻工作的时间间隔为零
B.双代号网络计划中关键节点的最早时间与最迟时间相等
C.双代号网络计划中所有关键工作的自由时差全部为零
D.单代号搭接网络计划中关键线路上相邻工作的时距之和最大
答案:A 解析:
B:当工程网络计划的计算工期小于计划工期时,关键线路上的工作的总时差就不为零了,所以双代号网络计划中关键节点的最早时间与最迟时间不相等 B错;
C:既然关键线路上的工作的总时差不为零,关键工作的自由时差不可能为零,所以C 错。
D:在关键线路上,单代号搭接网络计划中关键线路上相邻工作的时距之和都应该最小。所以D错。
【例题8·单选】单代号搭接网络的计算工期由( )决定。
A.终点虚拟节点的最早完成时间
B.最后开始的工作的最早完成时间
C.最后一项工作的持续时间
D.可能由中间某个工作的最早完成时间
答案:D 解析:根据单代号搭接网络计划时间参数的计算过程,我们应知道,其计算工期可能由中间某个工作的最早完成时间来决定.
【例题9·单选】在搭接网络计划中,工作之间的搭接关系是由( )决定的。
A.工作的持续时间 B.工作的总时差 C.工作之间的时间差值 D.工作的间歇时间
答案:C 解析:在搭接网络计划中,工作之间的搭接关系是由相邻两项工作之间的不同时距决定的。所谓时距,就是在搭接网络计划中相邻两项工作之间的时间差值。
【例题10·单选】在道路工程中,当路基铺设工作开始一段时间后,只要提供了足够的工作面,路面浇筑工作即可开始,则路基铺设工作与路面浇筑工作之间的时间差值称为( )搭接关系。
A.FTS B.STS C.FTF D.STF文章来源:https://www.toymoban.com/news/detail-410124.html
答案:B 解析:根据题意,它是从开始到开始的关系。所选B。文章来源地址https://www.toymoban.com/news/detail-410124.html
到了这里,关于关键路径、工期、总时差和自由时差精讲的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!