数据降维之主成分分析法PCA-Toy模板网

这篇具有很好参考价值的文章主要介绍了数据降维之主成分分析法PCA。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

主成分分析法PCA

参考链接：https://www.bilibili.com/video/BV1E5411E71z

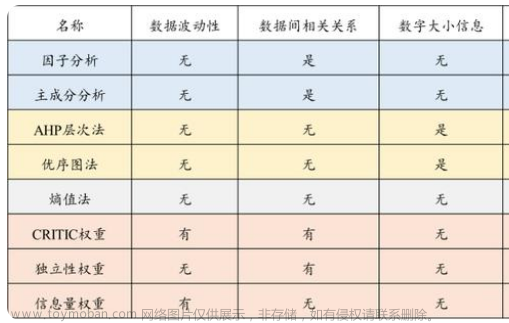
主成分分析（Principal Component Analysis，PCA），是一种统计方法。通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量，转换后的这组变量叫主成分。

在用统计分析方法研究多变量的课题时，变量个数太多就会增加课题的复杂性。人们自然希望变量个数较少而得到的信息较多。在很多情形，变量之间是有一定的相关关系的，当两个变量之间有一定相关关系时，可以解释为这两个变量反映此课题的信息有一定的重叠。主成分分析是对于原先提出的所有变量，将重复的变量（关系紧密的变量）删去多余，建立尽可能少的新变量，使得这些新变量是两两不相关的，而且这些新变量在反映课题的信息方面尽可能保持原有的信息。

设法将原来变量重新组合成一组新的互相无关的几个综合变量，同时根据实际需要从中可以取出几个较少的综合变量尽可能多地反映原来变量的信息的统计方法叫做主成分分析或称主分量分析，也是数学上用来降维的一种方法。

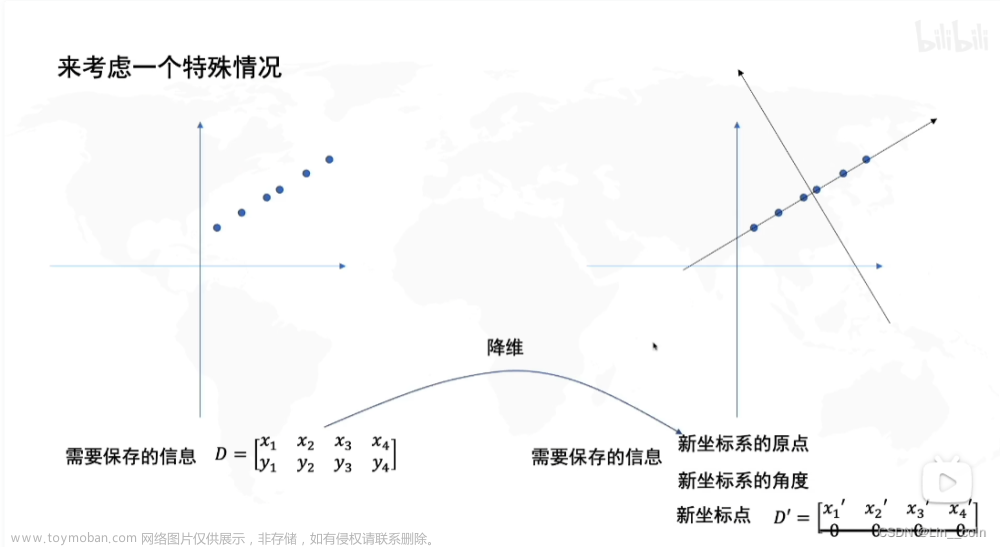
二维投一维

PCA目的：找到一个坐标系，使得这个数据再只保留一个维度时，信息损失最小（可以理解为数据点投射到新坐标系上，数据最分散）。

数据降维之主成分分析法PCA

怎么样找到最好的新坐标系：

找到数据分布最分散的方向（方差最大），作为主成分（坐标轴）

步骤

去中心化

为什么要去中心化？

在一般的实际问题当中，我们要分析的数据一般是多个维度的，由多个特征或者属性构成的复杂数据集合。例如对某个地区的人均收入构建预测模型或者进行分析的时候，我们会考虑到该地区的GDP总量、人口数量、税收等，显然它们的单位或者说是数量级都是不一样的。我们通过中心化将各类数据整合在原点附近，使其统一起来便于后续处理。也可以进一步进行标准化处理，使得各类数据在每个维度上的取值范围都相同。

如何进行去中心化？
数据降维之主成分分析法PCA
上式中，x是原始样本数据，μ是样本期望，通过上述变换，我们得到期望是0的新的样本数据集。

标准化的方法：
数据降维之主成分分析法PCA
在去中心化的基础上除以原始样本数据的标准差，我们得到期望是0，标准差是1的新的样本数据集（这样的数据集符合正态分布）。

中插小知识

白数据：x和y都符合标准正态分布且xy不相关

我们手中的数据经过去中心化以后：xy都符合正态分布但是表示标准，且xy相关

（拉伸决定了方差最大的方向）（旋转决定了方差最大的方向的角度）

数据降维之主成分分析法PCA

所以我们要求找到的就是这样一个坐标系，也就是旋转的角度，也就是R。

结论：协方差矩阵的特征向量就是R。

求协方差矩阵

协方差表示的是两个变量在变化过程中是同方向变化还是反方向变化？同向或反向的程度如何？

1、方差：[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ipEyGUvp-1654950728624)(https://www.zhihu.com/equation?tex=s%5E2+%3D+%5Cfrac%7B1%7D%7Bn-1%7D%5Csum_%7Ba%7D%5E%7Bb%7D%7B%28x_i-%5Cbar+x%29%5E2%7D)]

2、协方差：[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-fuSrtFaT-1654950728624)(https://www.zhihu.com/equation?tex=%CF%83%28x%2Cy%29+%3D+%5Cfrac%7B1%7D%7Bn-1%7D%5Csum_%7Ba%7D%5E%7Bb%7D%7B%28x_i-%5Cbar+x%29%28y_i-%5Cbar+y%29%7D)]

3、协方差矩阵：数据降维之主成分分析法PCA

白数据的协方差矩阵是：

数据降维之主成分分析法PCA

因为我们去中心化数据的期望为0，所以我们手中的数据的协方差矩阵是：

数据降维之主成分分析法PCA

协方差矩阵的特征向量和特征值

因为C‘为2*2矩阵且两行不相关，所以至少有两个特征向量。

数据降维之主成分分析法PCA

为什么协方差矩阵的特征向量就是R？

数据降维之主成分分析法PCA

我们将D’通过R-1去旋转回原本角度，发现其协方差是L。

所以特征值就是作用于这个矩阵之后只产生拉伸效果不产生旋转效果的的基向量。

≈两个轴方向的方差。

数据降维之主成分分析法PCA

一个小案例

根据中学生身体四项指标，身高(X1)，体重(X2)，胸围(X3）和坐高(X4)。

(1）试对附件数据的30名学生的数据进行主成分分析;

(2)计算各学生在各主成分上得分，并对其可视化显示和聚类(可划分为三类);

X = [148 41 72 78;
139 34 71 76;
160 49 77 86;
149 36 67 79;
159 45 80 86;
142 31 66 76;
153 43 76 83;
150 43 77 79;
151 42 77 80;
139 31 68 74;
140 29 64 74;
161 47 78 84;
158 49 78 83;
140 33 67 77;
137 31 66 73;
152 35 73 79;
149 47 82 79;
145 35 70 77;
160 47 74 87;
156 44 78 85;
151 42 73 82;
147 38 73 78;
157 39 68 80;
147 30 65 75;
157 48 80 88;
151 36 74 80;
144 36 68 76;
141 30 67 76;
139 32 68 73;
148 38 70 78];
% 矩阵相关系数
R = corr(X);
% 求矩阵的行
n = size(X,1);
% 对矩阵进行归一化（标准化变换）
XZ = (X-ones(n,1)*mean(X,1))*inv(sqrt(diag(var(X,1))));
% 对标准化矩阵XZ求相关系数矩阵R
R1=XZ'*XZ/size(X,1);
% eiv为特征向量 eic为特征值
[eiv,eic]=eig(R);
eiv(:,2)=-eiv(:,2);
% 将标准化后的指标变量转化为主成分Uij即Z
Z=XZ*eiv(:,1:2);
% Z(:,1)第一列 Z(:,2)第二列
% 画散点图
scatter(Z(:,1),Z(:,2),'*')
% hold on主要是用于添加新绘图的时候保留当前绘图
hold on;
% 对散点图上每一个点稍右方添加文本内容
for k=1:n
    text(Z(k,1)+0.1,Z(k,2),{k});
end
Z;

多维

参考链接：https://zhuanlan.zhihu.com/p/44453206

将思路推广到多维数据，原始数据不再只有一列，也就是指标不只有一个，设原始样本有 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-cNy1tqJw-1654950728629)(https://www.zhihu.com/equation?tex=p)] 个指标，每个指标有 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-AcbQwc8X-1654950728629)(https://www.zhihu.com/equation?tex=n)] 个观察值，这就是一个 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-XAKaLC4x-1654950728630)(https://www.zhihu.com/equation?tex=n%5Ctimes+p)] 维矩阵。

将上述矩阵转换为 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-02lYkioz-1654950728630)(https://www.zhihu.com/equation?tex=m)] 个新指标 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-wLiJvhyR-1654950728632)(https://www.zhihu.com/equation?tex=F_i%2C+i+%3D+1%2C+2%2C+…%2C+m)] [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-7oP5PEPy-1654950728632)(https://www.zhihu.com/equation?tex=%E4%B8%94m+%3C+p)] 。

数据降维之主成分分析法PCA

转换成如下形式：

数据降维之主成分分析法PCA

协方差与目标

参考文章PCA的数学原理，使用两个字段 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-kUlP22D0-1654950728634)(https://www.zhihu.com/equation?tex=a%EF%BC%8Cb)] 来说明问题，矩阵形式为

数据降维之主成分分析法PCA

进行如下形式的计算

数据降维之主成分分析法PCA

我们可以看到，对角元素为方差，非对角元素为协方差，且 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-biiznN7M-1654950728635)(https://www.zhihu.com/equation?tex=%5Cfrac%7B1%7D%7Bm%7DXX%5E%7BT%7D)] 为对称矩阵，并可推广到一般形式 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-VfvV8kkz-1654950728636)(https://www.zhihu.com/equation?tex=C+%3D+%5Cfrac%7B1%7D%7Bm%7DXX%5E%7BT%7D)] ，不仅限于二维。

根据我们的目标，主要是想让方差最大，且协方差为0，也就是将上述矩阵 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-treaoXLa-1654950728636)(https://www.zhihu.com/equation?tex=C)] 进行对角化。

设最终的矩阵为 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-WdNzFNz9-1654950728637)(https://www.zhihu.com/equation?tex=F)] ，也就是我们要找的降维后的指标矩阵，变换矩阵为 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-RtfFWixu-1654950728637)(https://www.zhihu.com/equation?tex=P)] ，则 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-1qrBYZxc-1654950728637)(https://www.zhihu.com/equation?tex=F+%3D+PX)] 。 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-cFkBEebq-1654950728638)(https://www.zhihu.com/equation?tex=F)] 对应的协方差矩阵为 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-dcV2Nzgy-1654950728638)(https://www.zhihu.com/equation?tex=D)] ，那 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-yIseKtsp-1654950728638)(https://www.zhihu.com/equation?tex=D%E4%B8%8EC)] 的关系为

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-YZefwthQ-1654950728639)(https://www.zhihu.com/equation?tex=D+%3D+%5Cfrac%7B1%7D%7Bm%7DFF%5E%7BT%7D+%3D+%5Cfrac%7B1%7D%7Bm%7D%28PX%29%28PX%29%5E%7BT%7D+++++%3D+%5Cfrac%7B1%7D%7Bm%7DP%28XX%5E%7BT%7D%29P%5E%7BT%7D+%3D+PCP%5E%7BT%7D)]

最终的 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-M3cqnADo-1654950728639)(https://www.zhihu.com/equation?tex=PCP%5E%7BT%7D)] 是一个对角阵，且元素从大到小排列， [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-yG7Zgz4r-1654950728640)(https://www.zhihu.com/equation?tex=P)] 的前 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-dzLfI9rb-1654950728640)(https://www.zhihu.com/equation?tex=k)] 行就是我们要找的基，这样就达到了降维的目的，即

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-0sMnL0V4-1654950728640)(https://www.zhihu.com/equation?tex=P_%7Bk%5Ctimes+m%7D+%5Ctimes+X_%7Bm+%5Ctimes+n%7D+%3D+F_%7Bk%5Ctimes+n%7D)] 。

协方差矩阵 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-y1xwoMfy-1654950728641)(https://www.zhihu.com/equation?tex=C)] 是对称矩阵，对称矩阵有非常好的性质：

① 实对称矩阵不同特征值对应的特征向量必然正交。

② 设特征向量 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Vix2i2wV-1654950728641)(https://www.zhihu.com/equation?tex=%5Clambda)] 重数为 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-pIao26z6-1654950728642)(https://www.zhihu.com/equation?tex=r)] ，则必然存在 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-njPiZXRQ-1654950728642)(https://www.zhihu.com/equation?tex=r)] 个线性无关的特征向量对应于 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-hOWnsmDM-1654950728643)(https://www.zhihu.com/equation?tex=%5Clambda)] ，因此可以将这 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-A7NAZFJz-1654950728643)(https://www.zhihu.com/equation?tex=r)] 个特征向量单位正交化。

也就是说 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-JLWMTLbU-1654950728644)(https://www.zhihu.com/equation?tex=n)] 维对称矩阵一定可以找到 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-0E9SPUw8-1654950728647)(https://www.zhihu.com/equation?tex=n)] 个单位正交的向量，使得该矩阵成对角矩阵，即：

数据降维之主成分分析法PCA

则让 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-J3IXOpoB-1654950728651)(https://www.zhihu.com/equation?tex=P+%3D+E%5E%7BT%7D)] 即可达到降维的目的。

实例

参考链接：https://zhuanlan.zhihu.com/p/454447043

某金融服务公司为了了解贷款客户的信用程度，评价客户的信用等级，采用信用评级常用的 5C(能力，品格，担保，资本，环境)方法对15名客户进行打分，由此判断客户违约的可能性。

品格:指客户的名誉；
能力:指客户的偿还能力；
资本:指客户的财务实力和财务状况；
担保:指对申请贷款项担保的覆盖程度；
环境:指外部经济政策环境对客户的影响；

数据降维之主成分分析法PCA

由于各项指标的难易程度不同，因此需要对5项指标进行赋权，以便能够更加合理的对15名客户进行评价。

数据处理

计算每一列的平均值

数据降维之主成分分析法PCA

计算每一列的标准差

数据降维之主成分分析法PCA

例如能力该指标，我们计算其标准差 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-UaHvQ2kC-1654950728654)(https://www.zhihu.com/equation?tex=%5Csigma_%7Bi%7D%5E%7B2%7D%3D%5Cfrac%7B%2866-64%29%5E%7B2%7D%2B%2865-64%29%5E%7B2%7D%2B…%2B%2864-64%29%5E%7B2%7D%7D%7B15-1%7D%3D2.7775+)]

数据标准化处理

数据降维之主成分分析法PCA

例如客户1的能力该项指标，使用公式: [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-0z5BNWFQ-1654950728654)(https://www.zhihu.com/equation?tex=z_%7Bji%7D%3D%5Cfrac%7Bx_%7Bji%7D-%5Cmu_%7Bi%7D%7D%7B%5Csigma_%7Bi%7D%7D%3D%5Cfrac%7B66-64%7D%7B2.7775%7D%3D0.7201)]

计算相关系数矩阵

数据降维之主成分分析法PCA

例如品格与能力的相关系数，使用公式 :[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-GV4DbpVJ-1654950728656)(https://www.zhihu.com/equation?tex=r_%7Bij%7D%3D%5Cfrac%7B0.7201%2A%28-0.0699%29%2B0.3600%2A%28-0.4198%29%2B…%2B%28-0.7201%29%2A%28-0.4198%29+%7D%7B15-1%7D%3D0.8817+)]