求二叉树中,任意两个节点之间的距离最大值是多少?
提示:本节仍然是重点说二叉树的DP递归套路,非常重要而且容易理解
二叉树的动态规划树形DP递归套路系列文章有这些,可以帮助你快速掌握树形DP的题目解题思想,就一个套路:
(1)判断二叉树是否为平衡二叉树?树形DP,树形动态规划的递归套路
题目
请你求一颗二叉树中,任意两个节点之间的距离最大值是多少?
所谓二叉树节点a与b之间的距离,是从a走到b点,一共有多少个点,包括a和b在内。
一、审题
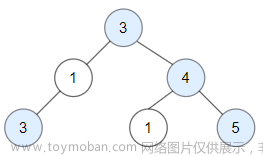
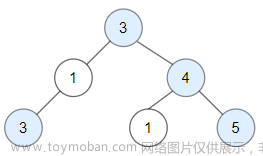
示例:下图所示:AB两点距离为4
AC两点距离为6
CD两点距离为5
AC两点和AD两点都是6
故整个二叉树,最大距离为6
本题的二叉树节点和树
public static class Node{
public int value;
public Node left;
public Node right;
public Node(int v){
value = v;
}
}
//构造一颗树,今后方便使用
public static Node generateBinaryTree(){
//树长啥样呢
// 1
// 2 3
// 4 5 6 7
// 8
// 9
Node head = new Node(1);
Node n2 = new Node(2);
Node n3 = new Node(3);
head.left = n2;
head.right = n3;
Node n4 = new Node(4);
Node n5 = new Node(5);
n2.left = n4;
n2.right = n5;
Node n6 = new Node(6);
Node n7 = new Node(7);
n3.left = n6;
n3.right = n7;
Node n8 = new Node(8);
n4.left = n8;
Node n9 = new Node(9);
n8.left = n9;
return head;
}
二、树形动态规划的递归套路:树形DP的递归套路
95%的二叉树动态规划问题,都可以用以下套路解决:
一、定义个信息类:Info
收集x左树和右树都有的信息(左右树都有哦,而不是针对某单独的左树或者右树),比如是否平衡?树的高度,总之就是有的信息,不管你是String还是Boolean还是Integer类型的信息。经常是要讨论与x有关,还是 与x无关。
二、树形DP递归套路: 来到x节点
1)base case:考虑叶节点应该返回的信息Info
2)先收集左树和右树的信息Info
3)综合2)整理x自己的信息,并返回;
三、从题目给的二叉树head开始求(2),得到了一个head的信息Info,找里面咱们要用的那个信息:比如是否平衡?
返回它。
来,咱们举例说明:实践知真理!
解题思路:求二叉树中任意两个节点间最大距离
95%的二叉树动态规划问题,都可以用以下套路解决:
一、定义个信息类:Info
收集x左树和右树都有的信息(左右树都有哦,而不是针对某单独的左树或者右树),比如是否平衡?树的高度,总之就是有的信息,不管你是String还是Boolean还是Integer类型的信息。经常是要讨论与x有关,还是与x无关。
本题,是要分析以x开头的二叉树,下面究竟那两个点间的距离为最大值
那么我来讨论一下:
(1)这个最大距离路径,经过x,与x有关。比如这种下面这种情况,咱们如何求AB之间的距离?
AB必须经过x,则,咱是这样求距离的,x的左树高度h1=1,右树高度h2,加自己这个节点,就是距离,即h1+h2+1;
显然,既然你要统计距离用到了高度信息,所以咱们Info中就要收集高度信息。
这最大距离一定要经过x节点么?
不一定,万一不经过呢?
(2)最大值不经过x节点的情况,下面这样,如何求AB之间的距离呢?
这图中,求x开头的树,里面最大距离是多少?自然CB经过x,距离为6,但是抵不过不经过x那条路径AB=7
所以呢,我在求x开头的树的最大距离时,左树上最大距离为d1,右树上最大为d2=AB=7,这俩最大值max(d1,d2)就是咱要的结果。
综合一下,x节点为头的树,上面最大距离是多少?max(上面情况(1),上面情况(2))
即max(h1+h2+1,d1,d2)
因此,咱们可以看出,去一颗树上你除了收集树的高度信息之外,你还需要收集什么信息?你这个树上原有的最大距离是多少?maxDistance。
所以定义Info为:
public static class Info{
public int height;//高
public int maxDistance;//树的最大距离
public Info(int h, int max){
height = h;
maxDistance = max;
}
}
二、树形DP递归套路: 来到x节点
//递归找信息——直到头结点
public static Info process(Node x)
1)base case:考虑叶节点应该返回的信息Info
本题中,base仍然时遇到叶节点的null,怎么返回信息
叶节点上,高度0,最大距离自然也是0,故:return new Info(0, 0);//终止到叶节点,啥都是0呗
2)先收集左树和右树的信息Info
这很简单,就是x节点左右收集信息即可
Info leftInfo = process(head.left);
Info rightInfo = process(head.right);
3)综合2)整理x自己的信息,并返回;
——综合x节点的高度信息,很简单,左右树最高高度+1,就是x自己的节点高度
——综合最大值信息,这也很明了:上面说过了即max(h1+h2+1,d1,d2)
左右高度和+1
d1是左树已具备的最大距离,与x无关的
d2是右树已具备的最大距离,与x无关的
把这两个信息整合好之后,返回;return new Info(height, maxDistance);
三、从题目给的二叉树head开始求(2),得到了一个head的信息Info,找里面咱们要用的那个信息:比如是否平衡?
返回它。
调用?咱们要的就是Info中的最大距离,不管你经过x也好,还是不经过x也罢,咱要的就是最大距离。
Info info = process(head);
return info.maxDistance;//返回最大值
手撕代码,固定套路很简单吧:
//复习
public static Info f(Node x){
if (x == null) return new Info(0,0);//高度为0,最大距离为0
//左右拿信息
Info left = f(x.left);
Info right = f(x.right);
//整合Info
int height = Math.max(left.height, right.height) + 1;
int max = left.height + right.height + 1;//途径x这条
//不途径x这条
max = Math.max(max, Math.max(left.maxDistance, right.maxDistance));//仨一起比
return new Info(height, max);
}
//调用
public static int btMaxDistance(Node head){
if (head == null) return 0;
Info info = f(head);
return info.maxDistance;
}
public static void test(){
Node cur = generateBinaryTree();
int max = getMaxDistanceOfBinaryTree(cur);
System.out.println(max);
int max2 = btMaxDistance(cur);
System.out.println(max2);
}
public static void main(String[] args) {
test();
}
//树长啥样呢
// 1
// 2 3
// 4 5 6 7
// 8
// 9
结果:
7
7
显然就是9 8 4 2 1 3 7 长度为7呗
咱再做一个不经过head的最大距离验证:
//构造一颗树,今后方便使用
public static Node generateBinaryTree2(){
//树长啥样呢
// 1
// 2 3
// 4 5
// 8 6
// 9 7
// 10
Node head = new Node(1);
Node n2 = new Node(2);
Node n3 = new Node(3);
head.left = n2;
head.right = n3;
Node n4 = new Node(4);
Node n5 = new Node(5);
n2.left = n4;
n2.right = n5;
Node n6 = new Node(6);
Node n7 = new Node(7);
n5.right = n6;
n6.right = n7;
Node n8 = new Node(8);
n4.left = n8;
Node n9 = new Node(9);
n8.left = n9;
Node n10 = new Node(10);
n7.right = n10;
return head;
}
public static void test(){
Node cur = generateBinaryTree();
int max = getMaxDistanceOfBinaryTree(cur);
System.out.println(max);
int max2 = btMaxDistance(cur);
System.out.println(max2);
Node cur2 = generateBinaryTree2();
int max3 = btMaxDistance(cur2);
System.out.println(max3);
}
public static void main(String[] args) {
test();
}
//树长啥样呢
// 1
// 2 3
// 4 5
// 8 6
// 9 7
// 10
7
7
8
看见没,压根与节点1无关那条路径,9 8 4 2 5 6 7 10 总长度为8,这才是大距离
因此,本题涉及的二叉树动态规划的DP递归套路,是不是很强大。
尽量只讨论与x有关还是无关,然后收集信息,这个信息时每棵树都通用的信息,不分左右,然后整理我们x节点需要的信息,返回
最后一定会拿到head的信息,然后取我们要的结果。
总结
提示:重要经验:文章来源:https://www.toymoban.com/news/detail-410738.html
1)二叉树的动态规划DP递归套路,要熟练掌握,上面有系列文章,看它2个例子就明白了
2)二叉树的树形DP递归套路,往往要分析与x节点有关,还是与x节点无关,才能整理出信息来。
3)笔试求AC,可以不考虑空间复杂度,但是面试既要考虑时间复杂度最优,也要考虑空间复杂度最优。文章来源地址https://www.toymoban.com/news/detail-410738.html
到了这里,关于求二叉树中,任意两个节点之间的距离最大值是多少的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!