滑模控制理论(SMC)-Toy模板网

这篇具有很好参考价值的文章主要介绍了滑模控制理论(SMC)。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

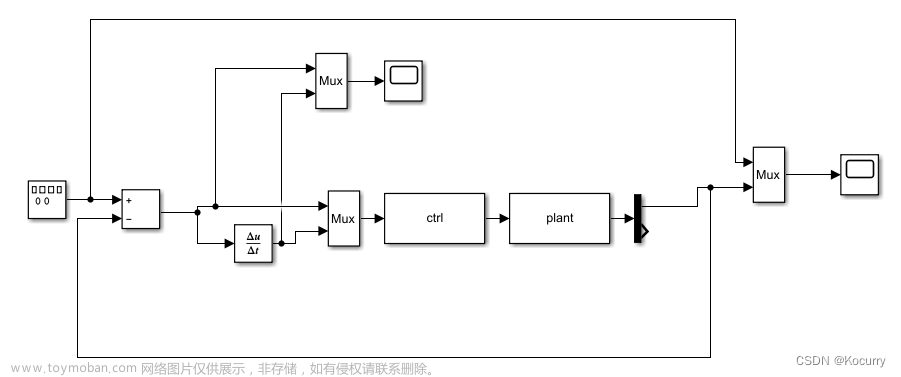
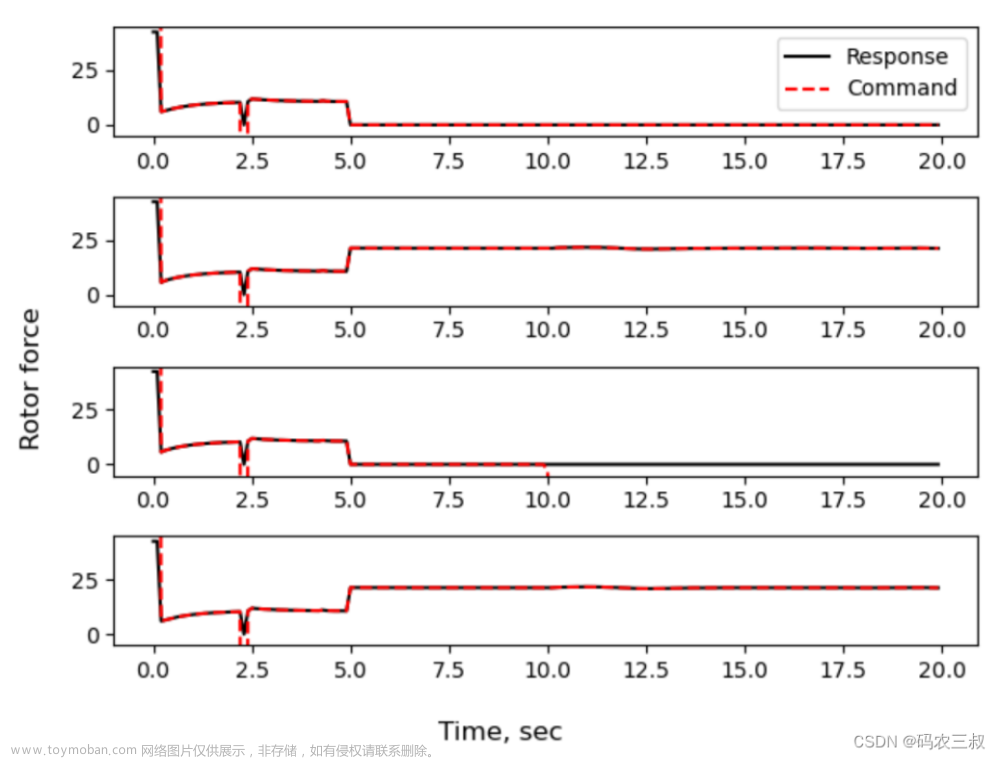
滑模控制理论(Sliding Mode Control,SMC)

滑膜控制理论是一种建立在现代控制理论基础上的控制理论，其核心为李雅普诺夫函数，滑膜控制的核心是建立一个滑模面，将被控系统拉倒滑模面上来，使系统沿着滑模面运动，滑膜控制的优势在于无视外部扰动和不确定性参数，采取一种比较暴力的方式来达到控制目的，但是这种暴力也带来了一些问题，就是正负信号的高频切换，一般的硬件是无法进行信号的高频切换的，所以需要一些其他的方式避免这个问题，还有就是型号的高频切换会导致输出的信号出现震荡，导致系统在所选取的滑模面之间来回震荡，这种震荡是无法消除的，这也是滑膜控制的一个问题。

优点

滑动模态可以设计

对扰动不敏感

缺点

硬件无法适应高频的信号切换

信号高频切换带来的输出信号震荡

系统建模

我们可以建立一个简单的二阶系统的状态方程
$\begin{align} \dot x_1 &= x_2 \nonumber \\ \dot x_2 &= u \nonumber \\ \end{align}$
我们的控制目标很明确，就是希望 $x_1 = 0,x_2=0$

设计滑模面

$s=cx_1+x_2$

这里有个问题就是，滑模面是个什么东西，为什么要设计成这个样子，为什么不是别的样子，其实这个涉及一个问题就是我们控制的目标是什么，是 $x_1 = 0,x_2=0$ ，那如果 $s = 0$ 呢
$\begin{equation} \begin{cases} cx_1 + x_2 = 0 \\ \dot x_1 = x_2 \\ \end{cases} \Rightarrow cx_1+\dot x_1 = 0 \Rightarrow \begin{cases} x_1 = x_1(0)e^{-ct} \\ x_2 = -cx_1(0)e^{-ct} \\ \end{cases} \nonumber \end{equation}$
可以看出状态量最终都会趋于0，而且是指数级的趋于0。 $c$ 越大，速度也就越快。所以如果满足 $s=cx_1+c_2=0$ ,那么系统的状态将沿着滑模面趋于零，（ $s = 0$ 称之为滑模面)

设计趋近律

上面说，如果 $s = 0$ 状态变量最终会趋于0，可以如何保证 $s = 0$ 呢，这就是控制率 $u$ 需要保证的内容了
$\dot s = c \dot x_1 + \dot x_2 = cx_2+u$
趋近律就是指 $\dot s$ ，趋近律的一般有以下几种设计
$\begin {cases} \dot s = - \varepsilon sgn(s), \varepsilon > 0 \\ \dot s = - \varepsilon sgn(s)-ks, \varepsilon > 0 , k>0\\ \dot s = - k|s|^{\alpha}sgn(s), 0 < \alpha < 1 \end{cases}$

$\begin{cases} 1,s>0 \\ -1,s<0 \\ \end{cases}$

根据以上的趋近律，我们就可以获得控制量 $u$ 了(选取第一种控制率)。
$-cx_2-\varepsilon sgn(s)$
我们对系统施加控制量 $u$ 即可保证系统最终稳定在原点。

证明有效性

在控制原理中用李雅普诺夫函数来判断系统的稳定性，对于系统状态方程 $\dot s = cx_2+u$ ，我们此时的目标已经是希望把系统拉倒滑模面附近了，控制目标是 $s$ ,对于 $s$ 如果存在一个连续函数 $V$ 满足下面两个式子，那么系统将在平衡点 $s = 0$ 处稳定，即 ${\lim\limits_{t \to \infty}V = 0}$
${\lim\limits_{|s| \to \infty}V = \infty}$

$\dot V < 0 \ for \ s \ne 0$

我们证明的方法就是令 $\frac {1} {2} s ^ 2$ ，很明显我们满足第一个条件，我们对 $V$ 进行求导，
$\dot V = s \dot s = -s \varepsilon sgn(s) = - \varepsilon|s| < 0$
也是满足第二个条件的，所以最终系统会稳定在滑膜面附近，这也就意味着两个变量也会稳定在滑模面期望他们稳定在的位置，即零点。

无限时间问题

上面的分析看似无懈可击，实际上是没什么用的，因为我们最终得到的结论是，在时间趋于无穷时，系统的状态必将趋于0，这有用吗，并没有，因为无限时间这太恐怖了，人死了系统都没稳定的话这没什么意义，所以我们必须要求他是有限时间可达的，所以我们修改一个李雅普诺夫的第二个条件
$\dot V \le - \alpha V ^ {\frac {1} {2}}$
对于改进后的这个条件可以分离变量再积分
$\begin {align} \frac {\text d V} {\text d t} &\le - \alpha V ^ {\frac {1} {2}} \nonumber\\ V ^ {- \frac {1} {2}} \text d V &\le - \alpha \text d t \nonumber\\ \int^{t}_{0} V ^ {- \frac {1} {2}} \text d V &\le \int^{t}_{0} - \alpha \text d t \nonumber\\ V ^ {\frac {1} {2}} (t) - V ^ {\frac {1} {2}} (0) &\le - \frac {1} {2} \alpha t \nonumber\\ V ^ {\frac {1} {2}} (t) &\le - \frac {1} {2} \alpha t + V ^ {\frac {1} {2}} (0) \nonumber \\ \end {align}$
根据上面的等式可以看出， $V$ 将在有限时间达到稳定，稳定的最终时间为
$t_r \le \frac {2V^ \frac {1} {2} (0)} {\alpha}$
因为李雅普诺夫条件的改变，控制器 $u$ 也需要作出相应改变
$\begin{cases} \dot V = s \dot s = -s \varepsilon sgn(s) = - \varepsilon|s|\\ V = \frac {1} {2} s ^ 2 \\ \dot V \le - \alpha V ^ {\frac{1} {2}} \end{cases} \Rightarrow \dot V = - \varepsilon|s| \le -\alpha \frac{s}{\sqrt {2}} \Rightarrow \varepsilon \ge \frac {\alpha} {\sqrt{2}}$
也就是给之前随意指定的 $\varepsilon$ 增加了一个控制条件

干扰问题

上面的讨论其实还基于一个假设，没有干扰，没有干扰的控制是非常好做的，也是没什么实际意义的，这里我们将干扰项加入状态方程，之前我们讲到了滑膜方法对干扰是不敏感的，这里我们将从原理上解释为什么滑膜方法对干扰不敏感。

加入干扰后的状态方程
$\begin{align} \dot x_1 &= x_2 \nonumber\\ \dot x_2 &= u + d \nonumber\\ \end{align}$
这对我们设计滑膜面没有什么影响，我们的滑膜面如下
$s = cx_1+x_2$
我们的趋近律设计也不变
$\dot s = - \varepsilon sgn(s)$
我们的控制量 $u$ 也不变
$\varepsilon sgn(s) - cx_2$

$\begin{align} \dot s &= c \dot x_1 + \dot x_2 \nonumber\\ &=cx_2 + u + d \nonumber\\ \end{align}$

分析稳定性我们依旧使用李雅普诺夫函数
$\begin{align} V &= \frac {1} {2} s ^ 2 \nonumber\\ \dot V &= s \dot s \nonumber\\ &= s (cx_2 + u + d) \nonumber\\ &= s (- \varepsilon sgn(s) + d) \nonumber\\ & \le -\varepsilon|s| + sd \nonumber\\ & \le -\varepsilon|s| + sL \nonumber\\ & \le |s|(\varepsilon - L) \nonumber\\ \end{align}$
其中 $L$ 为干扰 $d$ 的上界
$\begin{align} \dot V &\le - \alpha V ^ {\frac{1} {2}} \nonumber\\ -\varepsilon|s| + sL & \le -\alpha \frac{s}{\sqrt {2}} \nonumber\\ -\varepsilon|s| & \le -\alpha \frac{s}{\sqrt {2}} - sL \nonumber\\ \varepsilon|s| & \ge \alpha \frac{s}{\sqrt {2}} + sL \nonumber\\ \varepsilon & \ge sgn(s)(\frac{\alpha}{\sqrt {2}} + L) \nonumber\\ \varepsilon & \ge (\frac{\alpha}{\sqrt {2}} + L) \nonumber\\ \end{align}$
所以我们直接证明了，当我们的干扰有上界的情况下，我们的滑膜参数 $\varepsilon $ 只需要满足上述条件就可以以指数级的收敛速度收敛到滑膜面附近。

三阶系统滑膜设计方法示例

三阶系统的模型如下
$\begin {align} \dot x_1 &= x_2 \nonumber\\ \dot x_2 &= x_3 \nonumber\\ \dot x_3 &= f(x) + g(x)u \nonumber\\ \end {align}$
假设，我们期望的 $x_1$ 的目标是 $x_{1d}$ ，注意，这里和前文不同，这里的控制目标不在是0了
$\begin{align} e_1 &= x_1 - x_{1d} \nonumber\\ e_2 &= \dot e_1 = \dot x_1 - \dot x_{1d} = x_2 - \dot x_{1d} \nonumber\\ e_3 &= \dot e_2 = \ddot x_1 - \ddot x_{1d} = x_3 - \ddot x_{1d} \nonumber\\ \end{align}$
设计滑模面
$s = c_1 e_1 + c_2 e_2 + e_3$
设计李雅普诺夫函数
$\frac{1}{2} s ^ 2$
对李雅普诺夫函数进行求导
$\begin{align} \dot V &= s \dot s \nonumber\\ &= s (c_1 \dot e_1 + c_2 \dot e_2 + \dot e_3) \nonumber\\ &= s (c_1 e_2 + c_2 e_3 + x_3 - \ddot x^{(3)}_{1d}) \nonumber\\ &= s (c_1 e_2 + c_2 e_3 + x_3 - f(x) + g(x)u - x^{(3)}_{1d}) \nonumber\\ &= s (\Gamma - f(x) + g(x)u - x^{(3)}_{1d}) \nonumber\\ &= sg(x)(\frac {\Gamma - f(x) - x^{(3)}_{1d}} {g(x)} + u) \nonumber\\ \end{align}$
这里我们设计趋近律
$\dot s = - \varepsilon sgn(s) = \Gamma - f(x) + g(x)u - x^{(3)}_{1d}$
得到控制量 $u$
$\frac {-\varepsilon sgn(s) - \Gamma + f(x) + x^{(3)}_{1d}} {g(x)}$
带入李雅普诺夫函数可得
$\dot V = -s \varepsilon sgn(s) = -\varepsilon |s| \le 0$
这里可以看到系统必将稳定，如果需要控制到达稳定的时间就限制 $\varepsilon$ 即可文章来源地址https://www.toymoban.com/news/detail-411009.html