《LKD3粗读笔记》(6)内核数据结构

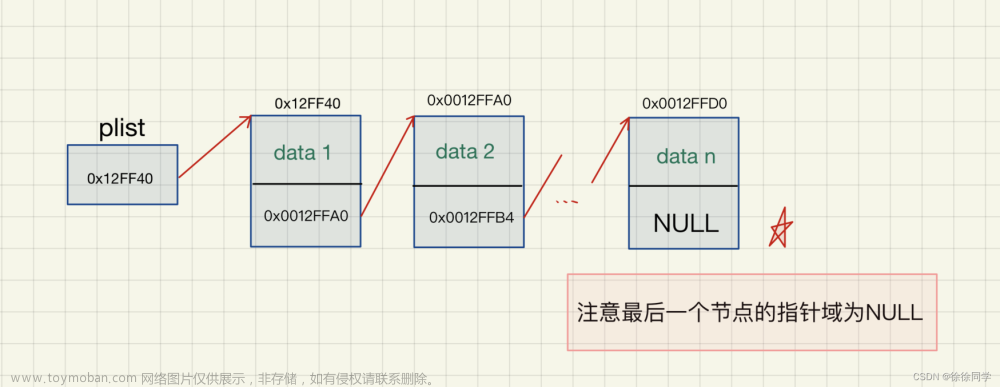
1、链表

1. 单向链表和双向链表
   这里涉及到了对void关键字的理解：C高级编程——关于void类型的解释
   • 链表的特点
     • 链表是一种存放和操作可变数量元素（常称为结点）的数据结构
     • 与静态数组不同的是，链表所包含的元素都是动态创建并插入链表的，在编译时不必知道具体创建多少个元素。
     • 链表中每个元素创建时间不同，它们在内存中无需占用连续内存区。
   • 简单的单向链表结构

     /*一个链表中的某个结点*/
     struct list_element {
     	void *data; 				/*有效数据*/
     	struct list_element* next;	/*指向后一个元素的指针*/
     }
     

   • 简单的双向链表

     /*一个链表中的某个结点*/
     struct list_element {
     	void *data; 				/*有效数据*/
     	struct list_element* next;	/*指向前一个元素的指针*/
     	struct list_element* prev;	/*指向后一个元素的指针*/
     }
     

2. 环形链表
   • 链表首尾相连。
   • Linux内核的标准链表采用的环形双向链表，因为环形双向链表提供最大的灵活性。
3. 沿链表移动
4. Linux内核中的实现
   1. 链表数据结构

      • Linux内核中链表的实现方式是什么样的？
        它不是将数据结构塞入链表，而是将链表结点塞入数据结构。
        eg：举个小狐狸的例子
        官方提供的链表代码在头文件<linux/list.h>中声明：

        struct list_head{
        	struct list_head* next;
        	struct list_head* prev;
        };
        

        现在，将这个链表结点塞入小狐狸这个数据结构：

        struct fox{
        	unsigned long tail_length; 	/*狐狸尾巴长度*/
        	unsigned long weight;     	/*狐狸重量*/  
        	bool sex;					/*狐狸性别*/
        	struct list_head list;      /*所有fox结构体形成链表*/
        };
        

        那么，整个链表大概就是这个样子（画的真丑）：
        
        使用绘图工具重新绘制如下：
        

      • 内核提供的链表操作例程有什么特点，是如何实现的？

        • 链表操作方法统一的特点是：只接受list_head结构作为参数
        • 使用container_of宏可以很方便地从链表指针找到父结构中包含地任何变量。
        • container_of宏要实现什么功能？
          已知结构体type的成员member的地址ptr，求解结构体type的起始地址。
        • container of函数的具体实现？

          #define container_of(ptr, type, member) ({              \        
          const typeof( ((type *)0)->member ) *__mptr = (ptr);    \  //自行思考该行的作用       
          (type *)( (char *)__mptr - offsetof(type,member) );})  //type的起始地址 = ptr - size
          

          其中offsetof函数原型为：

          #define offsetof(TYPE, MEMBER) ((size_t) &((TYPE *)0)->MEMBER)
          

          详解请看：container of()函数简介、Linux内核中的container_of函数简要介绍、C语言高级用法—typeof()关键字
        • 依靠list_entry()方法，内核提供了创建、操作以及其他链表管理的各种例程。list_entry()方法本质上就是container_of宏的套壳：

          #define list_entry(ptr, type, member) \
          container_of(ptr, type, member)
          

          典型的是:以小狐狸为例，有了这个方法之后，我们可用通过结构体list_head获得他的“宿主”也就是fox结构体了。
   2. 定义一个链表
      • 链表的定义有3种方式，它们都是通用的

        #define LIST_HEAD_INIT(name) { &(name), &(name) }
        
        #define LIST_HEAD(name) \
        	struct list_head name = LIST_HEAD_INIT(name)
        
        static inline void INIT_LIST_HEAD(struct list_head *list)
        {
        	list->next = list;
        	list->prev = list;
        }
        

      • 运行时初始化链表(最常见的方式，因为多数元素是动态创建的)
        eg：以前面的小狐狸为例，运行时初始化链表的方式为：

        struct fox *red_fox;
        red_fox = kmalloc(sizeof(*red_fox),GFP_KERNEL);
        red_fox  -> tail_length = 40;
        red_fox  -> weight = 6;
        red_fox  -> sex = MAN;
        INIT_LIST_HEAD(&red_fox -> list);
        

      • 编译器静态初始化结构体

        struct fox red_fox = {
        	.tail_length = 40,
        	.weight = 6,
        	.sex = MAN,
        	.list = INIT_HEAD_LIST(red_fox.list)
        };
        

   3. 链表头
      • 内核链表最杰出的特性是什么？
        所有的链表节点都包含有一个list_head指针，我们可以从任何一个节点起遍历链表，直到遍历完所有节点。
      • Linux内核通常采取什么方式遍历链表？
        Linux内核使用一个特殊指针索引到整个链表，这个特殊的索引节点也是一个常规的list_head:

        static LIST_HEAD(fox_list); //再次以小狐狸为例
        

5. 操作链表(增加、删除、移动和合并节点)
   内核提供了一组函数来操作链表，这些函数都要使用一个或多个list_head，所有这些函数的复杂度都为O(1)。
   1. 向链表中增加一个节点
      • 给链表增加一个节点：

        list_add(struct list_head *new,struct list_head *head)
        

        该函数向指定链表的head结点后插入new节点。
      • 把节点增加到链表尾部：

         list_add_tail(struct list_head *new,struct list_head *head)
        

        该函数向指定链表的head结点前插入new节点。你可以想象一下，你把任何一个结点当作head（Linux采用的是双向环形链表），那么head结点的前一个结点就是尾结点，实际上就是在这个尾结点插入新的结点，插入的位置也就是头节点的前面。
   2. 从链表中删除了一个节点
      这里涉及到了对内联函数的理解，请参考：inline的作用
      • 函数原型：

         list_del(struct list_head *entry)
        

        该函数从链表中删除entry元素。
      • 链表删除函数代码具体实现：

         //把当前删除的节点的前驱和后继分别交给后节点和前节点，但并没有释放对应的内存。
        static inline void __list_del (struct list_head* prev,struct list_head* next){
        	next -> prev = prev;
        	prev -> next = next;
        }
        static inline void list_del(struct list_head *entry){
        	__list_del(entry -> prev,entry -> next);
        }
        

        该函数仅仅是将entry元素从链表移走，所以该函数被调用后，通常需要再撤销包含entry的数据结构体和其中的entry项目。
   3. 移动和合并链表节点
      • 把节点从一个链表移到另一个链表。

        list_move(struct list_head *list,struct list_head *head);
        

        该函数从一个链表中移除list项，然后将其加入另一链表的head节点后面。

        list_move_tail(struct list_head *list,struct list_head *head);
        

        与list_move()类似，不同点在于这里将list项插入到head项前面。
      • 判断链表是否为空

        list_empty(struct list_head *head);
        

        如果指定的链表为空，该函数返回非0值；否则返回0
      • 合并两个未连接的链表

        list_splice(struct list_head *list,struct list_head *head);
        

        该函数合并两个链表，它将list指向的链表插入到指定链表的head元素后面。

        list_splice_init(struct list_head *list,struct list_head *head);
        

        与list_splice()类似，不同点在于由list指向的链表需要重新被初始化。
   4. 节约两次提领（dereference）
      如果已经得到了next和prev指针，那么可以直接调用内部链表函数，这样可以省下一点时间。
      *eg:*以链表删除函数为例：
      可以调用内部函数__list_del(prev,next)代替调用外部包装函数list_del(list)。
6. 遍历链表
   1. 基本方法
      遍历链表最简单的方法是使用list_for_each()宏，该方法的核心是使用了list_entry()方法。以小狐狸为例：

      struct list_head *p;  //链表头（前面有提及）
      struct fox *f;  //小狐狸结构体
      
      /*遍历链表，输入参数为用于指向当前项的临时变量p 以及 链表的链表头list_head*/
      list_for_each(p,&fox_list){ 
      	//本质上是通过链表节点得到fox结构体指针。
      	f=list_entry(p,struct fox,list);// 输入参数分别是：临时变量p、结构体类型 以及 当前结构体变量的成员
      }
      

   2. 可用的方法
      多数内核代码采用list_for_each_entry()宏遍历链表。该宏内部也使用list_entry()宏，但简化了过程：

      list_for_each_entry(pos,head,member)
      //pos:可以看作是list_entry()的返回值
      //head:指向头节点的指针（链表头）
      //member:list_head结构的变量名
      

   3. 反向遍历链表
      使用宏list_for_each_entry_reverse()实现反向遍历链表，使用的方法和list_for_each_entry()是相同的。

      list_for_each_entry_reverse(pos,head,member)
      

      • so，为什么要使用反向遍历链表？
        • 性能原因——当搜寻的节点在当前节点之前，使用反向遍历方法会更快。
        • 实现堆栈数据结构，从链表的尾部遍历，实现LIFO。
   4. 遍历的同时删除
      使用list_for_each_entry_safe()方法实现遍历时删除：

      list_for_each_entry_safe(pos,next,head,member);
      

      注意，开发人员需要通过在潜在的删除操作前存储next（或者previous ）指针到一个临时变量中，以便执行删除操作。
      此外，你可以通过list_for_each_entry_safe_reverse()方法反向遍历链表并删除，具体操作原理和list_for_each_entry_safe类似，故不赘述。
      • 注意点：
        需要在删除数据操作时锁定链表， 因为可能有多个进程并发地执行删除操作。
   5. 其他链表方法
      在<linux/list.h>中可以找到。

2、队列

任何操作系统内核都少不了一种编程模型：生产者和消费者。该模型必须使用队列来实现。标准的队列如图所示：

Linux内核通用队列实现成为kfifo(也就是kernel_fifo)，它实现在文件kernel/kfifo.c中，声明在文件<linux/kfifo.h>中。

1. kfifo
   • kfifo对象维护了两个偏移量： 入口偏移和出口偏移。入口偏移是指下一次入队列时的位置（即队尾），出口偏移是指下一次出队列时的位置（即队头）。当入口偏移等于出口偏移的时候，说明队列空了。注意： 出口偏移总是小于等于入口偏移
   • kfifo提供了两个主要操作： enqueue(入队列)和dequeue(出队列)。enqueue操作拷贝数据到队列的入口偏移位置，操作完后入口偏移随之加上推入的元素数目。dequeue操作从队列中出口偏移处拷贝数据，操作完成后出口偏移随之减去摘取的元素数目。
2. 创建队列
   • 动态创建队列

     int kfifo_alloc(struct kfifo *fifo,unsigned int size,gfp_t gfp_mask);
     

     该函数创建并且初始化一个大小为size的kfifo,内核使用gfp_mask标识来分配队列（后面章节会讲到）。如果成功kfifo_alloc()返回0
   • 用户自行分配缓冲区

     void kfifo_init(struct kfifo *fifo,void *buffer,unsigned int size);
     

     该函数创建一个kfifo对象，他将使用由buffer指向的size大小的内存。
   • 静态创建队列

     DECLARE_KFIFO(name,size);
     INIT_KFIFO(name);
     

     上述方法会创建一个名为name，大小为size的kfifo对象。
3. 推入队列数据

   unsigned int kfifo_in(struct kfifo *fifo,const void *from,unsigned int len)
   

   该函数把from指针所指的len字节数据拷贝到fifo所指的队列中。如果成功，则返回推入数据的字节大小。如果队列空间不足，则返回可用空间的大小。
4. 摘取队列数据
   • 摘取数据（类似于剪切）

     unsigned int kfifo_out(struct kfifo *fifo,const void *from,unsigned int len);
     

     该函数从fifo所指向的队列中拷贝出长度为len字节的数据到to所指向的缓冲中。如果成功，则返回拷贝的数据长度。如果队列中数据大小小于len，则返回可用空间的大小。
   • 查看数据（类似于复制）

     unsigned int kfifo_out_peek(struct kfifo *fifo,void *to,unsigned int len,unsigned int offset);
     

     该函数和kfifo_out()类似，但是这波操作类似于拷贝而非剪切，参数offset指向队列中的索引位置，也就是拷贝的起始位置。
5. 获取队列长度
   • 获得存储kfifo队列的空间的总体大小（以字节为单位），可调用方法kfifo_size()：

     static inline unsigned int kfifo_size(struct kfifo *fifo);
     

   • 获得存储kfifo队列中已经推入的数据大小：

     static inline unsigned int kfifo_len(struct kfifo *fifo);
     

   • 获得存储kfifo队列中剩余空间大小：

     static inline unsigned int kfifo_avail(struct kfifo *fifo);
     

   • 判断队列是空或者是满：

     static inline int kfifo_is_empty(struct kfifo *fifo);
     static inline int kfifo_is_full(struct kfifo *fifo);
     

6. 重置和撤销队列
   • 重置kfifo，即抛弃所有队列的内容，调用kfifo_reset():

     static inline void kfifo_reset(struct kfifo *fifo);
     

   • 撤销一个使用kfifo_alloc()分配的队列，调用kfifo_free():

     void kfifo_free(struct kfifo *fifo);
     

   • 撤销使用kfifo_init()方法创建的队列，需要负责释放相应的缓冲。

3、二叉树

• 什么是树？什么是二叉树？
  • 树，是一个能提供分层的树形数据结构的特定数据结构。在数学意义上，树是一个无环的、链接的有向图。任何一个节点有0或1个入边，0或多个出边。
  • 二叉树，是指每个节点最多只有2个出边的树。

1. 二叉搜索树

   • 什么是二叉搜索树？
     二叉搜索树(binary search trees,BST)，是一个节点有序的二叉树。
   • 二叉搜索树遵循什么法则？
     根的左分支节点值<根节点值<右分支节点值，所有的子树也都是二叉搜索树
   • 给出一个二叉搜索树的示例？
     

2. 自平衡二叉搜索树

   • 什么是平衡二叉树？
     所有叶子节点深度差不超过1的二叉搜索树。
   • 什么是深度？
     一个节点的深度是指从根节点起，到达它一共需经过的父节点数目。
   • 什么是高度？
     树中处于最底层节点的深度。
   • 什么是自平衡二叉树？
     指其操作都试图维持(半)平衡的二叉搜索树。
   • 平衡二叉树的示例？
     

3. 红黑树

   • 什么是红黑树？
     红黑树具有特殊的着色属性，是一种自平衡二叉搜索树，linux主要的平衡二叉树数据结构就是红黑树。
   • 红黑树遵循什么属性？
     ①所有叶子节点要么着红色，要么着黑色。
     ②叶子节点都是黑色。
     ③叶子节点不包含数据。
     ④所有非叶子节点都有两个字节点。
     ⑤如果一个节点是红色，则它的子节点都是黑色。
     ⑥在一个节点到其叶子节点的路径中，如果总是包含同样数目的黑色节点，则该路径相比其他路径是最短的。
   • 更多请自行搜索红黑树的数据结构

4. rbtree
   Linux实现的红黑树称为rbtree，该红黑树插入效率和树中结点数目呈对数关系。rbtree的搜索和插入操作需要自行实现。文章来源地址https://www.toymoban.com/news/detail-411107.html

   • 如何定义rbtree？
     rbtree的根节点由数据结构rb_root描述，创建一个红黑树，要分配一个新的rb_root结构，并且需要初始化为特殊值RB_ROOT.

     struct rb_root root = RB_ROOT;
     

     rbtree的其他节点由结构rb_node描述，给定一个rb_node，我们可以跟踪同名结点指针找到他的左右子节点。
   • 搜索
     eg ：实现在页高速缓存中搜索一个文件区(由一个i节点和一个偏移量共同描述)，每个i节点都有自己的rbtree，以关联在文件中的页偏移。下面函数搜索给定i节点的rbtree，以寻找匹配的偏移值。

     struct page *rb_search_page_cache(struct inode *inode,unsigned long offset)
     {
     	struct rb_node *n = inode -> i_rb_page_cache.rb_node;
     	while (n) {
     		struct page *page = rb_entry(n,struct page,rb_page_cache);
     		if (offset<page->offset)
     			n = n->rb_left;
     		else if (offset>page->offset)
     			n = n->rb_right;
     		else
     			return page;
     	}
     	returnNULL;
     }
     

     在while循环中遍历了整个rbtree, offset做比较操作，循环中找到一个匹配的offset节点，则搜索完成，返回page结构，遍历完全树都没找到，则返回NULL。
   • 插入
     eg ： 接上例进行插入操作。

     struct page *rb_insert_page_cache(struct inode*inode,unsigned long offset,struct rb_node*node)
     {
     	struct rb_node **p = &inode->i_rb_page_cache.rb_node;
     	struct rb_node *parent = NULL;
     	struct page *page;
     	while (*p) {
     		parent = *p;
     		page = rb_entry(parent,struct page,rb_page_cache);
     		if (offset<page->offset)
     			p= &(*p)->rb_left;
     		else if (offset>page->offset)
     			p= &(*p)->rb_right;
     		else
     			return page;
     	}
     	rb_link_node(node,parent,p);
     	rb_insert_color(node, &inode->i_rb_page_cache);
     	return NULL;
     }
     

     和搜索不同的是，该函数希望找不到匹配的offset，这样就可以插入叶子节点。找到插入点后，调用rb_link_node()(在给定位置插入新节点)，然后调用rb_insert_color()方法执行复杂的再平衡动作。如果页被加入到高速缓存中，则返回NULL。如果页原本已经存在高速缓存中，则返回这个已存在的页结构地址。

4、映射

• 用一个简单的例子来表示映射？
  比如，学生的学号与姓名就是一对映射，某人的身份证号和某人的支付宝余额是一对映射…
• 映射在数据结构中用什么实现？
  • 方法1：使用散列表（哈希表）实现，这种数据结构提供了键和值的映射关系，只要给出一个 key， 就可以高效查找到它所匹配的 value，底层通过数组实现，时间复杂度接近️ O(1)。
  • 方法2：使用自平衡二叉树实现，二叉搜索树在最坏的情况下能有更好的表现(对数复杂性相比线性复杂性)，自平衡二叉树同时满足顺序保证。
• 如何理解散列表和自平衡二叉树实现映射？
  • 对于散列表：因为底层是数组实现，所以我们可以这么认为：key是数组下标，实现映射的数据结构是数组，value就是对应的数组元素
  • 对于自平衡二叉树：我们可以这么认为：key是结点指针，实现映射的数据结构是自平衡二叉树，value就是对应的结点值
• Linux内核中如何实现映射？
  • 使用的是自平衡二叉树，它的目标是：映射一个唯一的标识数(UID)到一个指针。在下面的算法中，可以把UID理解为key，把idr理解为实现映射的数据结构，指针ptr理解为value。
  • 一个映射至少实现三种操作

    add (key, value)
    remove(key)
    value = lookup(key)
    

    除此之外，Linux还在add的基础上实现了allocate操作。这个allocate操作不但向map中加入了键值对，而且还产生UID。

1. 初始化一个idr
   调用void idr_init(struct idr *idp)方法。
   eg：

   struct idr id_huh;  /* statically define idr structure */
   idr_init(&id_huh);  /* initialize provided idr structure */ 
   

2. 分配一个新的UID
   • 如何分配UID？
     • 第一步：告诉idr需要分配新的UID，允许其在必要时调整后备树的大小。实现的方法是idr_pre_get()：

       int idr_pre_get(struct idr *idp, gfp_t gfp_mask)；
       //成功返回1,如果idr满，则报错-ENOSPC
       

       该函数在需要时调整由idp指向idr的大小。
     • 第二步：请求新的UID，并且将其加到idr，实现的方法是idr_get_new()。

       int idr_get_new(struct idr *idp, void *ptr,int *id)；
       //分配新UID关联到ptr上，UID存于id，成功返回0，错误返回-EAGAIN
       

   • 举个例子？

     int id;
     do {
     	if (!idr_pre_get(&idr_huh,GFP_KERNEL))
     		return-ENOSPC;
     	ret=idr_get_new(&idr_huh,ptr, &id);
     } while (ret== -EAGAIN);
     

     如果成功，上述片段代码将获得一个新的UID，他将被存储在整形变量id中，并且将UID映射到指针ptr 。
   • 有没有更严谨的请求UID算法？
     使用方法idr_get_new_above():

     int idr_get_new_above(struct idr *idp, void*ptr, int starting_id, int *id)；
     //可以指定一个最小UID，这样除了新的UID大于或等于starting_id外，还确保UID系统运行期间唯一
     

3. 查找UID关联的指针
   使用方法idr_find:

   void *idr_find(struct idr *idp, int id)；//通过idr和id寻找ptr
   //调用成功返回ptr指针，失败返回NULL，所以最好不要将UID映射到空指针，这样无法区分调用成功还是失败
   

   eg:

   struct my_struct *ptr=idr_find(&idr_huh,id);
   if (!ptr)
   	return-EINVAL; /* error */
   

4. 删除UID
   使用方法idr_remove()：

   void idr_remove(struct idr *idp, int id)；//id关联指针从映射中删除
   

5. 撤销idr
   撤销方法为idr_destroy():

   void idr_destroy(struct idr *idp)；
   //释放idr中未使用内存，而不释放当前分配给UID的内存。通常内核不会撤销idr，除非关闭或卸载。
   

   如果要撤销所有UID,则需要先执行方法idr_remove_all()，在执行方法idr_destroy()

   void idr_remove_all(struct idr *idp)；
   

5、数据结构以及选择

• 何时选择链表？
  • 对数据集合的主要操作是遍历数据
  • 需要存储相对较少的数据项
  • 需要和内核中其他使用链表的代码交互
  • 存储的大小不明的数据集合（可以动态添加任何数据类型）
• 何时选择队列？
  • 代码符合生产者/消费者模式
  • 想用一个定长缓冲（队列的添加和删除操作简单有效）
• 何时选择映射？
  • 需要映射一个UID到一个对象
    注意： Linux的映射接口是针对UID到指针的映射，并不适合其他场景。
• 何时选择红黑树？
  • 需要存储大量数据，并且迅速检索（时间复杂度为对数关系，链表的时间复杂度为线性关系）
    注意： 如果没有执行太多次时间紧迫的查找操作，则红黑树不是最好选择，可以用链表；

6、算法复杂度

• 一图解千愁

到了这里，关于《LKD3粗读笔记》(6)内核数据结构的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！