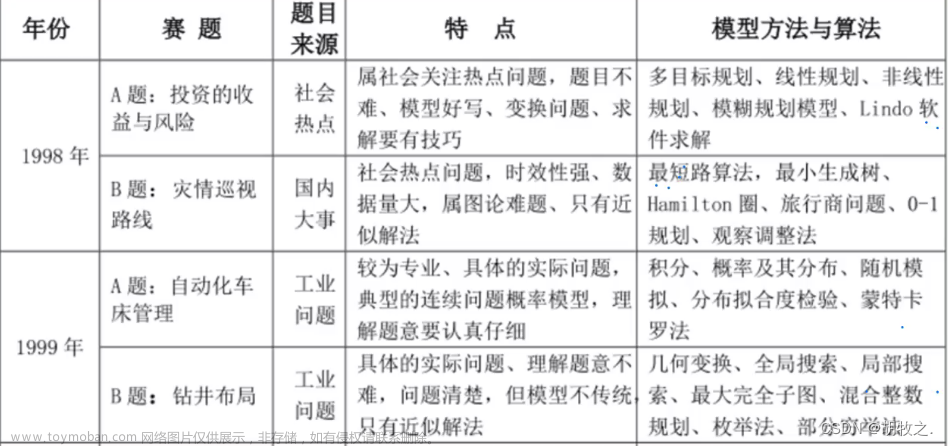
目录
模型的含义
模型的数学概念
模型的建立与求解
matlab代码实现
今天给大家讲解一下国赛中常用到的评价模型,模糊综合评价法。
模型的含义
模糊综合评价法是一种基于模糊数学的综合评价方法。该综合评价法根据模糊数学的隶属度理论把定性评价转化为定量评价,即用模糊数学对受到多种因素制约的事物或对象做出一个总体的评价。它具有结果清晰,系统性强的特点,能较好地解决模糊的、难以量化的问题,适合各种非确定性问题的解决。
那到底什么是模糊呢?我们不妨举一个例子:
在实际生活中,有许多概念难以用确定性的集合去描述。例如长与短,年轻与年老,美与丑,这些都是模糊的概念。怎样才算年轻,怎样才算年老?不同的人有不同的看法,“年轻”与“年老”还可以用岁数去量化它,那么“美”与“丑”,又要用怎样的一个指标去衡量这个概念呢?
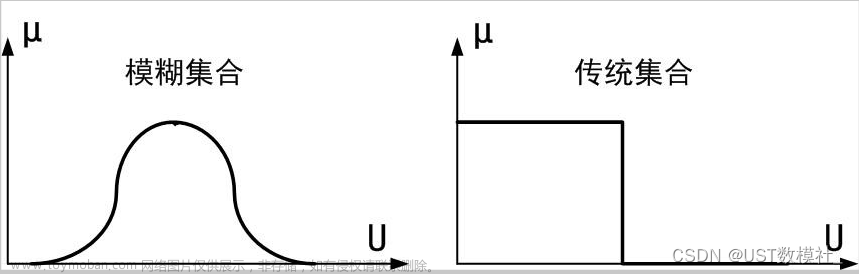
模糊数学就是用来处理涉及模糊概念的问题,尝试使用某种方法将模糊的概念量化,方便进行处理计算。模糊综合评价,自然就是模糊数学在评价类问题的一大应用了,也就是处理涉及模糊概念的评价类问题。
模型的数学概念
模糊集合:模糊集合是用来描述模糊性概念的集合,它与经典集合的区别之一是,模糊集合不具备确定性。例如资产超过500万,我们可以认为他富,也可以认为他穷。一般可分为偏小型,中间型以及偏大型。
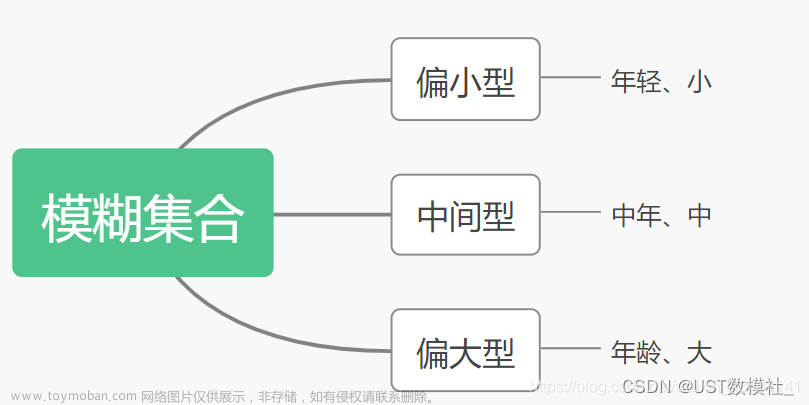
隶属度:我们使用“隶属度”来表示元素与模糊集合之间的关系,也就是元素隶属于模糊集合的程度。隶属度的范围通常在0到1之间,其值越大,就代表越属于这个集合。
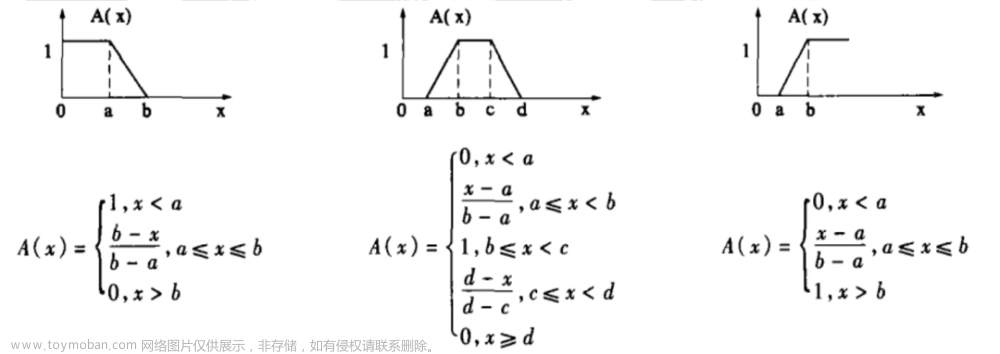
隶属函数:确定隶属函数,其实也就是给定一个模糊集合,之后再通过某些方法,给出我们需要研究的元素相对于该模糊集合的隶属度。下面介绍几种确定隶属函数的方法:
1、模糊统计法
简单的讲就是找个专家或者来个问卷调查,看一下专家给出的评断或者调查统计结果显示比如给一个东西质量打分,优秀占多少,良好占多少,差又占多少。

2、借助已有的客观尺度
对于某些模糊集合,我们可以用已经有的指标去作为元素的隶属度。例如判断小康家庭的恩格尔系数。

3、指派法
这是一个主观性比较强的方法,即凭主观意愿,在确定模糊集合的所属分类后,给它指派一个隶属函数,得到元素的隶属度。下图为梯型的隶属函数图像:
1、因素集(评价指标集)如:(德育、智育、文体)
2、评语集(评价的结果)如:(优、良、中等)
3、权重集(指标的权重)如:(0.3、0.6、0.1)
模型的建立与求解
以评价科研成果等级为例:
一、建立综合评价的因素集
评价集是评价者对评价对象可能做出的各种结果所组成的集合,通常用U表示,U={U1,U2,…Un},其中元素Vi代表影响评价对象的第i个因素。这些因素,通常都具有不同程度的模糊性。
对员工的表现,需要从多个方面进行综合评判,如科研成果的革新程度、安全性能、经济效益、推广前景等。所有这些因素构成了评价指标体系集合,即因素集,记为:U={革新程度U1,安全性能U2,经济效益U3,推广前景U4,成熟型U5}。
二、建立综合评价的评价集
评价集是评价者对评价对象可能做出的各种结果所组成的集合,通常用V表示,V={V1,V2,…Vm},其中元素Vj代表第j种评价结果,可以根据实际情况的需要,用不同的等级、评语或数字来表示。
对科研成果等级的评价有很好、较好、一般、不好等。由各种不同决断构成的集合称为评语集,记为:V={很好V1,较好V2,一般V3,不好V4}。
三、 进行单因素模糊评价,获得评价矩阵
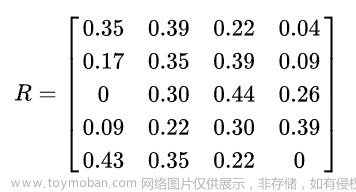
若因素集U中第i个元素对评价集V中第1个元素的隶属度为Ri1,则对第i个元素单因素评价的结果用模糊集合表示为:Ri={Ri1,Ri2,…Rin},以m个单因素评价集 R1,R2,…Rm为行组成矩阵Rm*n,称为模糊综合评价矩阵。
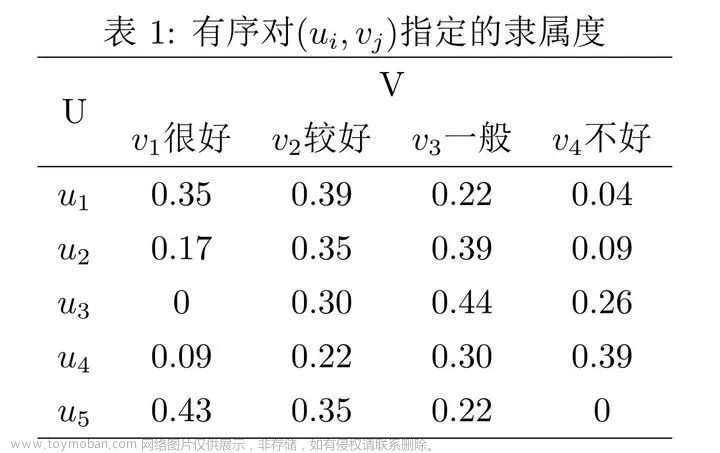
在实例中,某项科研成果通过专家评审打分,按下表给出U ×V 上每个有序对(Ui,Vj)指定的隶属度。
得到单因素评判矩阵R:
四、确定各因素的权重
评价工作中,各因素的重要程度有所不同,为此,给各因素Ui一个权重A1,各因素的权重集合的模糊集,用A表示:A={A1,A2,…An}。
在没有数据时,我们可以通过层次分析法确定权重;在有数据时,我们可以通过熵权法确定权重。在案例中,我们确定各因素的权重为:A={0.35,0.35,0.1,0.1,0.1}
五、建立综合评价模型
确定单因素评判矩阵R和因素权向量A之后,通过模糊变化将U上的模糊向量A变为V上的模糊向量B,即B=A1m*Rmn=(B1,B2,…Bn)。
在实例中,最后得到的模糊向量为B=A*R=(0.23,0.35,0.31,0.11),由计算结果可见,该成果应被评为二等奖。
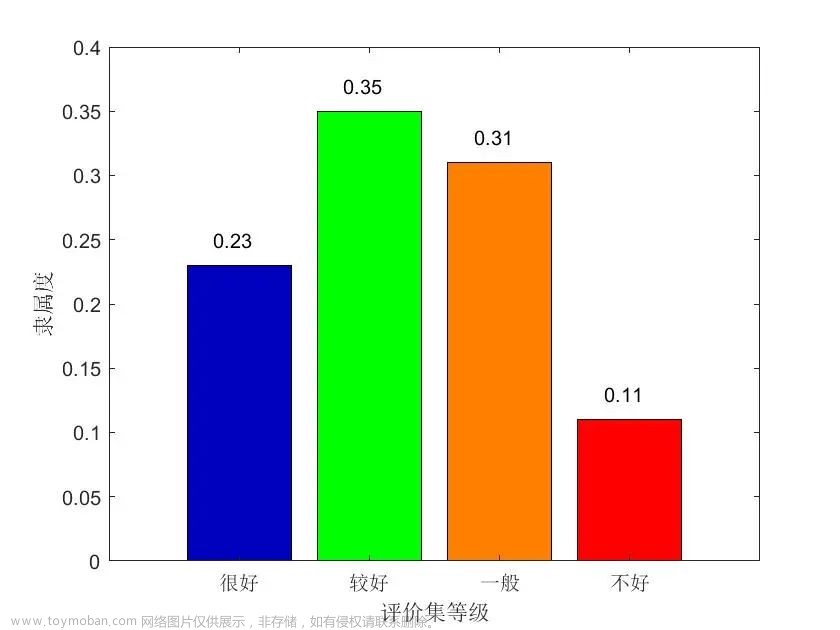
六、确定系统总得分
综合评价模型确定后,确定系统得分,即
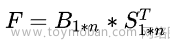
其中F为系统总得分,S 为V 中相应因素的级分。
在实例中,一等奖的级分肯定最高,其次是二等奖,依次往下,设级分依次为S=(100,80,60,30),则该成果最后的系统总得分为72.9。文章来源:https://www.toymoban.com/news/detail-411526.html
总的来说,模糊综合评价法就是先确定因素,评语和权重集,确定隶属函数后计算隶属度,组成判断矩阵,再由判断矩阵*权重集就能得到最后的综合评价向量了,数值最大的也就是最接近对应的评价的。文章来源地址https://www.toymoban.com/news/detail-411526.html
matlab代码实现
%% 模糊评判矩阵
R = [0.35 0.39 0.22 0.04
0.17 0.35 0.39 0.09
0 0.3 0.44 0.26
0.09 0.22 0.3 0.39
0.43 0.35 0.22 0]
%% 各因素的权重
A = [0.35 0.35 0.1 0.1]
%% 隶属度计算
B = A*R到了这里,关于数学建模常用算法—模糊综合评价的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!