在开关电源中，LLC谐振变换器是最常见的DC-DC变换器之一。 LLC谐振电路早在上世纪80年代就已经提出，到如今仍有广泛的应用，可见其优越性。其优点表现在：
1.LLC的开关器件能实现软开关，开关损耗小
2.效率高、功率密度大
LLC按结构的不同分为很多种，如对称半桥、非对称半桥、非对称全桥等。
非对称半桥LLC▲
对称半桥LLC▲
非对称全桥LLC▲
其中，非对称半桥LLC最为简单，所以本文以该电路为例讲解LLC的工作原理。
非对称半桥LLC▲
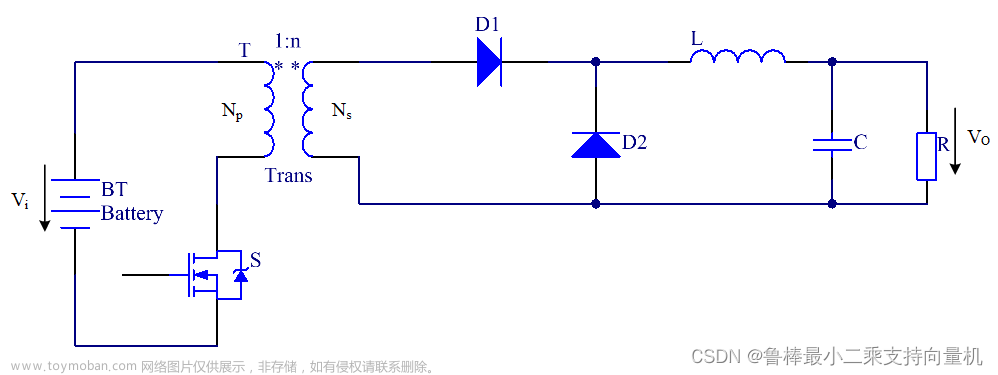
先来具体看看非对称半桥LLC电路的结构（如上）。开关管 Q1、Q2交替导通，在V1处产生方波。由于LLC的工作过程中，体二极管与结电容Cds也发挥了作用，所以将他们画出来了。Cr、Lr分别称为谐振电感、谐振电感。Lm并不是实际上的电感，而是变压器T的励磁电感，为了便于分析所以将其等效出来。Cr、Lr、Lm共同组成的部分，我们称之为谐振腔，它是LLC工作的核心部分，也是LLC名字的由来。变压器副边则是常见的桥式整流，变压器副边的电压是交流的，所以需要整流才能得到直流输出。当然也可以采用其他方式进行整流，例如带中心抽头变压器的全波整流。
§LLC基本工作原理：
LLC谐振变换器利用的是LC串联谐振特性来工作的。
如上电路，开关s初始状态是左侧接通，某时刻将s打到右边，在右侧由LC构成的环路中就会发生谐振。
谐振即环路中的电压电流以正弦波形变化，且电压电流相位相差90°，能量在电感与电容之间往复循环。假如不考虑环路中的电阻，电压电流会等幅震荡，即正弦波形的幅值保持不变。如果考虑实际电路的电阻，则会出现阻尼震荡，即正弦波形的幅值越来越小，直至变为0（如下）。显然，实际中的电路不可能没有电阻，所以要想维持谐振，就得用电源周期性给LC充能。
LC的谐振频率与L、C的数值有关，计算为：
如果利用开关管周期性给谐振腔的电感电容充电，维持谐振腔的谐振，交变的谐振电流流过变压器原边，就能在副边得到交变的感应电压，再经过整流就能得到直流输出了。如果需要调整输出电压，改变V1方波的频率（即改变Q1、Q2的开关频率），就能改变变压器副边的电压，达到输出电压调整的目的。这就是LLC变换器的基本原理。
谐振频率fr是LLC的核心参数，参数计算、稳压都是围绕fr。
§参数计算：
在进行LLC变换器设计时，有几个参数是必须要计算的：谐振频率、电压增益。直接关系到LLC的工作状态。
对于LLC谐振腔，含有两个电感，Lr是一定都会参与谐振的，但是对于Lm，其等效电感受变压器次级电路的影响。
所以我们需要考虑两种极限情况。1.变压器副边的负载无穷小，即副边开路。2.变压器副边的负载无穷大，即副边短路。如此，我们需要考虑两种情况，即Lm参与谐振、Lm不参与谐振。计算出两种情况下的谐振频率：
Lm不参与谐振时（第一谐振频率）：
Lm参与谐振时（第二谐振频率）：
定义两个系数：
式中f为开关频率
将LLC电路的FHA等效电路简化：
Rac是变压器副边电阻等效过来的，其值：
电压增益规定为变压器原边与输入电压的比值，即：
从简化电路可以看出，Lp与Rac电压相等，再把Cr与Ls看成一个整体，Vp其实就是Lp与Rac并联后在谐振电路的分压，即G
所以改变频率就会改变Vp，从而改变输出电压，这就是LLC的调压原理。
定义一个系数Q：
Q与Rac（上式中的Req）成反比，即输出负载R越大，Q越小（空载时，Q为0）；输出负载R越小，Q越大（输出短路时，Q为无穷大）。
根据稳压原理可以推出增益随频率变化函数关系：
如此，就得到LLC的增益曲线图：
不同的曲线代表不同的Q值，可以理解成不同的带载程度。可以发现随着Q增大，增益曲线的驼峰会远离Fr2，而靠近Fr1。
在fs=fr时（即开关频率等于谐振频率），所有曲线的增益都为1。这就是谐振的特点，当谐振腔工作在谐振点，其感抗的值等于容抗的值，即
此时两者刚好抵消，谐振电路中的阻抗有最小值，且等于电路中的阻值即Rac。相当于Vs1全部加在V上，即Vs1=Vp，所以增益为1。
增益曲线图可以分为3个工作区：ZCS区，ZVS区1，ZVS区2。对应不同的LLC工作的状态。因为开关管的开通损耗是比关断损耗大的，所以一般选择让LLC的开关管工作在ZVS区，即让开关频率在曲线波峰的右侧（如下图绿色加粗）。工作在ZVS区时，谐振腔整体成感性，电流滞后于电压。
如果输入电压不变，则输出电压与开关频率f的关系曲线和增益曲线一样。
可以发现，在ZVS区，频率fr越高，增益越小，即输出电压越小。
在进行LLC电路设计时，一般是根据输入输出电压范围，确定合适的变压器匝比以及谐振电容的容值，然后根据选择的谐振频率确定谐振电感的感量；再选择一个合适的K值，根据谐振电感确定变压器原边电感，再根据变压器磁芯选择合适的原副边匝数。
§LLC开关管的驱动：
不同于斩波电路通过PWM占空比调节输出电压，LLC谐振电路是通过调整开关频率调节电压（称之为PFM，脉冲频率调制）。
为了在V1处产生方波。Q1、Q2需交替导通，但是由于开关管开通与关断是需要时间的，无法做到瞬间完成，一旦在上管完全关断前，下管就开通，输出电源Uin就会通过上下管发生直连短路。所以为了避免该情况发生，需要在上下管的驱动间设置一个延时，即上管Q1关断后，延时t再开通下管Q2；同样，下管Q2关断后，延时t再开通上管Q1。我们称这个延时t为死区时间。在这个时间里，上下管G极电压都为0。
一般死区时间在几百ns。由于死区时间的存在，上下管驱动的占空比一定是小于50%的。
§ 软开关：
LLC效率高与其能实现软开关有关系，软开关减少了很多损耗。那么何为软开关？
现有如下电路：
理想中的开关管Q，在G极电压达到开通阈值电压后，DS极会立即导通，电压会立即降为零；在G极电压低于关断阈值电压后，DS极会立即截止，电流会立即降为零。
实际上的开关管不然。在G极电压达到开通阈值电压后，DS极并不会立即导通，而是有一个短暂的开通过程（可以理解为其电阻由很大变到很小），所以在开关管两端的电压会有一个短暂的下降过程，自然，流过其电流也会有一个短暂的上升过程（如下图a）。在这个过程中，开关管两端既有电压还有电流流过，所以就会有功率消耗在开关管上，这个过程消耗的能量就称为开通损耗，其值等于电压电流乘积的积分。
同样，在G极电压低于关断阈值电压后，DS极并不会立即截止，而是有一个短暂的关断过程（可以理解为其电阻由很小变到很大），所以在开关管两端的电压会有一个短暂的上升过程，自然，流过其电流也会有一个短暂的下降过程（如下图b）。在这个过程中，开关管两端既有电压还有电流流过，所以就会有功率消耗在开关管上，这个过程消耗的能量就称为关断损耗，其值也等于电压电流乘积的积分。
开通损耗与关断损耗统称为开关损耗。
在开关电源中，开关管都是以几十到几百kHz的频率工作，产生的开关损耗是非常大的。不仅影响开关电源的效率，还带来巨大的发热量。所以减小开关损耗是很有必要的。
软开关技术应运而生。
之所以叫“软”开关，是因为它的开关过程不会那么强硬，开关管只会在特定时机才开通或者关断。开通的时机就是开关管两端电压为0（我们称之为零电压开通ZVS，如下图a）；关断的时机就是流过开关管的电流为0（称之为零电流关断ZCS，如下图b）。
开通与关断时，开关管两端的电压与流过的电流不会发生交叠，所以消耗的功率就为0，也就不会有开关损耗了（由于开关管的内阻，仍会有少量工作损耗）。
但是对于上面的电路，电源U为直流源时，是无法实现软开关的，因为开关管开通时，其两端一定会有电压，关断时也一定会有电流。假如把直流源换成交流电压源呢（如下图b）？
如果在交流电压正半周开通，也是无法实现ZVS。但是交流电压一旦进入负半周，Q的体二极管就会导通，并将Q的DS极电压钳位在0.7V的固定压降（电流方向：S→D）。此时再通过G极开通，就能实现ZVS了。LLC的ZVC也是利用该原理实现的，只要在MOSFET通过体二极管反向导通时开通DS，就能实现ZVS。具体过程看下文的详细工作过程分析。
§LLC详细工作过程分析：
LLC工作过程相比反激比较复杂些，所以这里拆为很多阶段进行解析。
桥式整流无需多说，所以这里就不详细分析副边的情况。
参数：Vin=1000V，Rac=320Ω，Cr=0.05uF，Lr=20uF，Lm=100uF，fr1=159KHz，fr2=71.5KHz；开关频率：80KHz。
1. 初始状态-Q1导通、Q2关断（谐振腔状态：Cr、Lr、Lm储能）
初始状态下，Q1、Q2皆关断，Cr、Lr、Lm皆为零状态。0+时刻，上管Q1导通。此时谐振回路如上图加粗线所示。谐振电流Ir慢慢增加，谐振电容Cr电压升高，直到Cr电压等于输入电压Uin。该阶段波形如下（红框内）：
▲图例：CH1：Q1、Q2驱动； CH2：Q1、Q2电流； CH3：谐振电流Ir； CH4：谐振电容Cr电压
2.Q1导通、Q2关断（谐振腔状态：Lr、Lm释放能量，Cr继续储能）
当谐振电容Cr电压升高到等于Uin时进入该阶段。Cr电压等于Uin时，谐振电流达到最大值 并在这一阶段下降。Lr与Lm的感应电压反向，Cr继续充电，Cr电压升高。波形如下：
3.Q1关断、Q2关断（Lr、Lm继续释放能量，Cr继续储能）
Q1关断后，Q1所在回路断开，所以Q1的电流立即降为0。由于谐振电流Ir无法突变，仍保持顺时针流动，所以Q2的S极电压会高于D极，Q2的体二极管导通（方向：S极→D极），所以流过Q2的电流会立即增加到Ir。由于二极管的压降固定，所以Q2的电压被钳位在0.7V左右（Vs>Vd）。
Cr电压继续升高，Ir继续减小。
4.Q1关断、Q2开通（Lr、Lm继续释放能量，Cr继续储能）
Q1关断后，经过短暂的死区时间后Q2就会导通。因为在第3阶段时，Q2的体二极管导通，虽然其GS极本体未导通，但是其实与导通无异，Q2的GS极导通后，无非将压降进一步降低。所以谐振腔的情况仍与阶段3一样。注意：因为GS导通前，其两端电压已经为0.7V，Q2的ZVS就在这一步实现了。
在这阶段，Ir继续减小，Cr电压升高。
5. Q1关断、Q2开通（Lr、Lm储能，Cr释放能量）
上一阶段中，谐振电流Ir一直在减小，当其减小到0，相当于Lr与Lm储存的能量全部释放出来，而Cr的电压达到最大。然后，Cr会在这个阶段释放能量，电压下降，Lr与Lm储能。所以Ir会反向增大（波形如下）。直到Cr电压为0，进入下一阶段。
6.Q1关断、Q2开通（Lr、Lm释放能量，Cr储能）
谐振电容Cr电压降为0时，谐振电流Ir达到最大值。在这个阶段，Lr、Lm开始释放能量，Cr开始储能。Lr、lm、Cr电压全都反向。Ir开始反向减小，Cr电压上升（波形如下）。直到Q2关断，进入下一阶段。
7.Q1关断、Q2关断（Lr、Lm释放能量，Cr储能）
Q2关断前，谐振电流Ir以逆时针流动。Q2关断后，谐振电流无法突变，只能通过Q1的体二极管流过（方向：S极→D极）。Q1的体二极管压降将Q1的GS极电压钳位在0.7V。此时Uin相当于在吸收能量。
与上一阶段一样，Ir继续减小，Cr电压上升。直至Q1本体导通，进入下一个阶段。
8.Q1导通、Q2关断（Lr、Lm释放能量，Cr储能）
上一阶段Ir通过Q1的体二极管导通，虽然不是经过Q的本体，但实际上与GS导通无异，所以Q1的GS极导通后，谐振腔状态并不会因此发生变化，与上一阶段无异。
Ir继续减小，Cr电压上升（如下）。直至Ir=0，进入下一个阶段。
9.Q1导通、Q2关断，（Lr、Lm储能、Cr释放能量）
Ir减小到0之后，电流反向，Cr电压下降，Ir增大。直到Cr电压降至0，进入下一阶段。
10.Q1导通、Q2关断，（Lr、Lm、Cr储能）
这个阶段其实就是第2个循环的开始了，情况与第1阶段一致。只是这个阶段并不是从Q1开通开始，而是从Cr电压变为0开始。
这个阶段Ir增大，Cr电压升高，直至其电压等于Uin，然后进入下一阶段。
如此，单个周期过程已经讲解完成，后面不过是以此不断循环。
由于刚谐振时，能量传递未达到平衡，所以刚开始的波形不对称。经过足够的周期后，就会达到稳定状态，波形也会对称了如下。
§同步整流：
何为同步整流？
所谓同步整流就是区别于常规的二极管整流，取而代之的是MOSFET。通过采集MOS管DS电压来控制其导通与截止，以实现整流。
为什么需要同步整流？
二极管导通压降决定了不管输出电压多大，总是有0.7V的电压会被二极管"占用" 。对于一些输出低压大电流的情景（例如新能源汽车的车载DC-DC,输出电压一般为14V，但是电流可以达到100A），使用常规二极管作为整流器件 ，正向导通时会损耗大量能量，其值为电压电流乘积的积分，造成整体效率低，且给整流二极管的散热带来很大问题。
而MOSFET不存在导通压降的问题，其内阻也能做到5mΩ以下。如果使用MOSFET代替二极管整流，就能将损耗降到最低了。
如何实现？
二极管导通的条件是阳极对阴极的压降达到导通电压。
同样，只要我们采集MOSFET的D极对S极的压降，当压降为正，即Vd>Vs时，控制G极以导通MOSFET，反之则关断MOSFET，就能“模拟”二极管的导通特性，实现整流了。所以同步整流MOSFET还需要配合专门的控制电路。
篇幅有效，MATLAB仿真见下篇文章《更新中...》
觉得有用，可以点个赞哦~文章来源：https://www.toymoban.com/news/detail-411895.html
原创文章，转载请注明来源文章来源地址https://www.toymoban.com/news/detail-411895.html
到了这里，关于半桥LLC谐振变换器及同步整流MATLAB仿真（一）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
