高等工程数学 —— 第三章（2）奇异值分解和A的加号逆
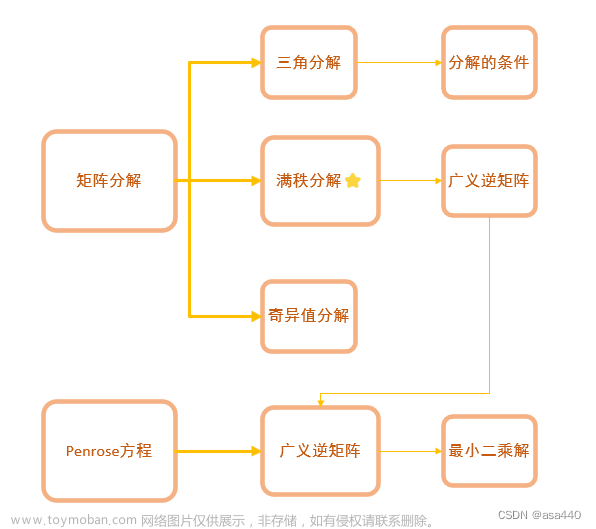
奇异值分解
首先来看什么是奇异值
也别管什么原理了，直接看方法和例题。盘它！
奇异值分解步骤：
- 这里就是先求 A H A A^{H}A AHA的特征值，然后求其特征向量并将每一个特征向量进行单位化得 V V V
- 然后看有几个非零特征向量就分出来几列当 V 1 V_1 V1
- 求出 U 1 U_1 U1后将其补全成方阵，因为是酉矩阵所以补的列向量要满足都两两单位正交
- 最后求 A A A时对 Σ \Sigma Σ的补全满足矩阵乘法就行，让补全后的 Σ \Sigma Σ矩阵的行数和 U U U矩阵的列数一样；补全后的 Σ \Sigma Σ矩阵的列数和 U U U矩阵的行数一样
看道例题好喽！
首先求
A
H
A
A^{H}A
AHA的特征值和特征向量来求
V
V
V
因为非零特征值有两个，所以取
V
V
V的前两列作为
V
1
V_1
V1来参与
U
1
U_1
U1的计算。
这里
U
1
U_1
U1已经是方阵了，所以不用补全了。对
Σ
\Sigma
Σ的补全满足矩阵乘法即可。
广义逆矩阵
- 这里其实就是当 A − 1 A^{-1} A−1不存在时，我们做的一个逆矩阵的推广
- 这里的四个公式我们把 X X X当作 A − A^{-} A−代入发现都成立。可见推广后的逆矩阵 A + A^{+} A+满足这四个条件用来某种程度上代替 A − A^{-} A−
A + A^{+} A+的直接计算方法
奇异值分解计算 A + A^{+} A+
- 注意奇异值分解得到的 U U U和 V V V可以是不一样的，但是相乘后得到 A + A^{+} A+的值是一样的。
例：
-
这里看 U U U补全的最后一列可知，我们补全的原则就是要满足两两正交的单位向量。
-
这里 V V V的列向量都是标准化后的单位向量
-
最后解出来的 A + A^{+} A+值是唯一的
满秩分解计算 A + A^{+} A+
对于行满秩矩阵和列满秩矩阵而言：
- 对于行满秩矩阵而言，满秩分解后 F = E F = E F=E，代入得上式。
- 对于列满秩矩阵而言，满秩分解后 G = E G = E G=E，代入得上式。
- 也不用刻意记，满秩分解完顺水推舟的化成这样了
例题：
- 注意这里要先求出括号里的 ( G G T ) − 1 (GG^T)^{-1} (GGT)−1和 ( F T F ) − 1 (F^TF)^{-1} (FTF)−1的值，然后将四个矩阵从左到右依次相乘。
- 看似满秩分解法求 A + A^{+} A+比奇异值分解求 A + A^{+} A+要简单一点，但是要求两个逆矩阵然后矩阵相乘到最后一大堆分数，恶心的很，呜呜呜呜。
- 注意求逆的时候只做初等行变换，笔者做题的时候傻了，有行有列的最后一直算不对，服了。
A + A^{+} A+的迭代计算方法
这部分我只能说不考，哈哈哈哈。这迭代应该是那种写计算机程序用的，而且这玩意书上一道题的没有。所以我们就简单列一下公式算了，嘻嘻。
Greville递推法
A + A^{+} A+的基本性质
A + A^{+} A+存在且唯一
同时满足以下性质：
广义逆矩阵的应用
例：
先用满秩分解求得
A
+
A^{+}
A+
文章来源：https://www.toymoban.com/news/detail-411906.html
文章来源地址https://www.toymoban.com/news/detail-411906.html
到了这里，关于高等工程数学 —— 第三章（2）奇异值分解和A的加号逆的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
