Dijkstra实现（邻接表C++版）-Toy模板网

这篇具有很好参考价值的文章主要介绍了Dijkstra实现（邻接表C++版）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

Dijkstra实现 —— 邻接表

1. 问题描述

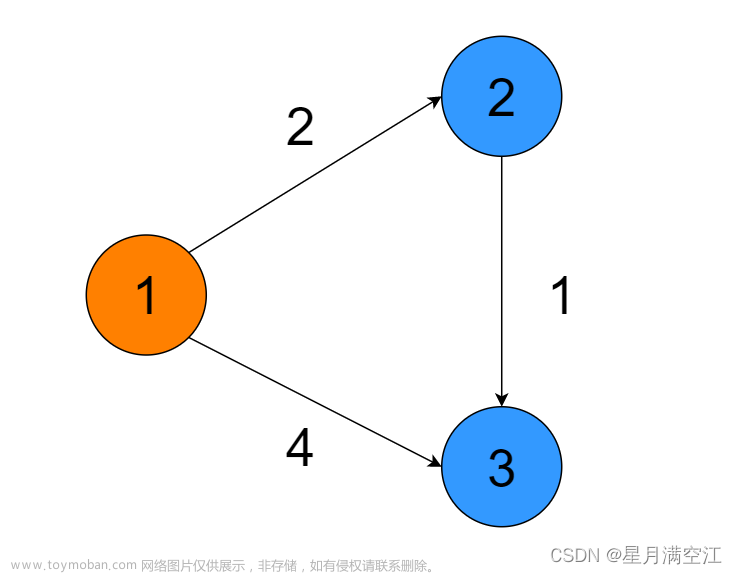
从V0出发，到各个节点的最短距离

Dijkstra实现（邻接表C++版）

2. 解决方法（Dijkstra算法）

1. 建立Dijkstra表

Dijkstra的过程，就是维护并更新一个表来实现的。

其中distance表示是从起始节点，到当前节点的距离。
path表示经过哪个节点达到当前节点。
表初始化为：path全-1，distance全为INT_MAX。

vertices	path	distance
0	-1	∞
1	-1	∞
2	-1	∞
3	-1	∞
4	-1	∞
5	-1	∞

2. 更新

2.1. 选择0（初始化）（假定从0出发）

vertices	path	distance
0	0	0
1	-1	∞
2	-1	∞
3	-1	∞
4	-1	∞
5	-1	∞

2.2 循环更新

每次选择一个新的节点，加入当前的连通分量中，其中选择的规则为：选择当前dis最小的节点（假设为节点Vk）。
将它加入连通分量，并使用它的相邻节点，更新distance，其中更新distance的原则是：
- 如果经过Vk，到达节点Vm的dis （即dis[Vk] + edge{Vk, Vm}）小于当前的dis[vm]，那么dis[vm] = dis[Vk] + edge{Vk, Vm}. （其中edge{Vk, Vm}表示Vk与Vm相连的边的长度）。

举例：从2.1表中，我们可以选择dis最小的节点，显然只有V0，将图中所有与V0相连的节点（即V1，V3，V4 节点）。

其中对于V1：dis[V0] + edge{V0, V1} = 0 + 1; 明显小于当前的dis[V1] = ∞，所以更新dist[1] = 1。V3，V4同理更新为4。

vertices	path	distance
0	0	0
1	0	1
2	-1	∞
3	0	4
4	0	4
5	-1	∞

再次选择一个新的节点：当前distance中最小的点是dis[1] = 1，将V1从dis中抹除（说明已经找到了从0到它的最小距离为1），将V1的所有相连节点加入的新dis计算出来（如果小于当前dis，就更新）：

new_dis_V3 = dis[V1] + edge{V1, V3} = 1 + 2 < dis[V3] = 4，因此更新dis[V3] = 2, 并且更新path为1。

vertices	path	distance
0	0	0
1	0	1
2	-1	∞
3	1	3
4	0	4
5	-1	∞

继续选择dis表中最小节点（其实这时候V0和V1这时候对应的0，1已经使用过了，将不被使用），这次选取的是V3对应的2，将V3的所有相连节点加入的新dis计算出来（如果小于当前dis，就更新）：
- new_dis_v2 = dis[V3] + edge{V3, V2} = 3 + 2 < dis[V2] = ∞，所以更新dis[2] = 5，并且将path[2]设置为3
- new_dis_v4 = dis[V4] + edge{V3, V4} = 3 + 3 > dis[V4] = 4，所以不更新dis[4]

vertices	path	distance
0	0	0
1	0	1
2	3	5
3	1	3
4	0	4
5	-1	∞

… 继续以上路径，可以得到最终结果

3. C++代码实现

3.0 代码设计

3.0.1 数据结构设计

图使用的是邻接表形式，即:

vector<vector<pair<int, int>>> graph; // 邻接表{from, {to, dis}} （即pair<int, int> = {to, dis}）

distance 和 path都是简单的数组结构：

vector<int> path;
vector<int> dis;

3.0.1 更新操作

dis需要经常更新（每次寻找最小的节点，将它删除，并将对应的节点插入）—— 可以用小根堆来做👇

注意：邻接表{from, {to, dis}} （即pair<int, int> = {to, dis}）。这里的cmp就是以pair中的第二个元素，即edg{Vk, Vm}的大小来判断在堆中的位置。

struct cmp{
    bool operator()(pair<int, int>& a, pair<int, int>& b) {
        return a.second < b.second;
    }
};

priority_queue<pair<int, int>, vector<pair<int, int>>, cmp> q;

3.0.2 代码的基本流程

1. 建立图 + 初始化

2. 一个循环，循环n次，更新dis和path

3. 输出结果，程序结束

3.1 代码 + 编译命令

完整的cpp代码如下👇（代码保存于Dijkstra.cpp中，编译命令为g++ Dijkstra.cpp -o dijkstra）文章来源地址https://www.toymoban.com/news/detail-412112.html

// g++ Dijkstra.cpp -o dijkstra

#include <bits/stdc++.h>
using namespace std;

vector<int> path;
vector<int> dis;
vector<vector<pair<int, int>>> graph; // 邻接表{from, {to, dis}} （即pair<int, int> = {to, dis}）

struct cmp{
    bool operator()(pair<int, int>& a, pair<int, int>& b) {
        return a.second < b.second;
    }
};

void print_vec(vector<int> &vec);
void print_graph();
void construct_graph(vector<vector<int>>& times, int n);
void dijkstra(int start);


int main() {
    vector<vector<int>> times = {
        {0, 1, 1},
        {0, 3, 4},
        {0, 4, 4},
        {1, 3, 2},
        {2, 5, 1},
        {3, 2, 2},
        {3, 4, 3},
        {4, 5, 3},
    };
    int n = 6;
    int start_id = 0;
    construct_graph(times, n);
    dijkstra(start_id);
    // print_vec(dis);
    exit(0);
}

void print_graph() {
    int n = graph.size();
    for (int i = 0; i < n; ++i) {
        cout << i << ": ";
        for (auto elem : graph[i]) {
            cout << "{" << elem.first << ", " << elem.second << "}, ";
        }
        cout << endl;
    }
}
void print_vec(vector<int> &vec) {
    for (auto elem : vec) {
        cout << elem << " ";
    }
    cout << endl << "---------------" <<endl;
}

// 构建图
void construct_graph(vector<vector<int>>& times, int n) {
    for (int i = 0; i < n; ++i) {
        graph.push_back(vector<pair<int, int>>());
    }
    for (auto edg : times) {
        graph[edg[0]].push_back({edg[1], edg[2]}); 
    }
}


void dijkstra(int start) {
    cout << "in dijkstra" << endl;
    // 初始化
    int n = graph.size();
    for (int i = 0; i < n; ++i) {
        path.push_back(-1);
        dis.push_back(INT_MAX);
    }
    dis[start] = 0;
    path[start] = start;

    priority_queue<pair<int, int>, vector<pair<int, int>>, cmp> q;
    q.push({start, 0});
    while (!q.empty()) {
        // cout << "q.size() = " << q.size() <<endl;
        int cur_id = q.top().first;
        int cur_dis = q.top().second;
        q.pop();

        // 说明已经访问过了
        if (cur_dis > dis[cur_id]) {
            continue;
        }

        // 将cur_id相邻的节点装入队列
        for (pair<int, int>& neighbor : graph[cur_id]) {
            int next_id = neighbor.first;
            int next_dis = dis[cur_id] + neighbor.second;
            if (next_dis < dis[next_id]) {
                dis[next_id] = next_dis;
                q.push({next_id, next_dis});
                path[next_id] = cur_id;
            }
        }
    }

    cout << "dis = ";
    print_vec(dis);

    cout << "path = ";
    print_vec(path);
}

3.2 运行结果：

levi@LEVI1:~/code$ g++ Dijkstra.cpp -o dijkstra
levi@LEVI1:~/code$ ./dijkstra 
in dijkstra
dis = 0 1 5 3 4 6 
---------------
path = 0 0 3 1 0 2 
---------------