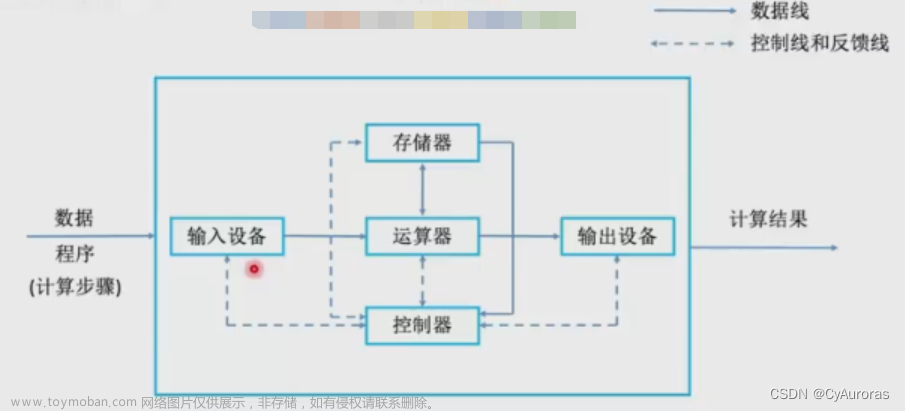
1、概述
消元法(elimination)也是计算机程序解方程的方法,消元法如果奏效了,方程就解出来了。
讨论消元法奏效和失效的情况。后半部分还介绍了 消元矩阵,即我们的消元运算在矩阵乘法中所表现的形式。并从消元矩阵引入,介绍了一些 逆矩阵 的基础知识。
2、使用 消元法 求解方程
2.1、消元法介绍
能够使用消元法分为以下 2 种情况:
- 成功: 矩阵的主元不包含 0, 也就是说,可逆矩阵。
- 失败: 矩阵的主元有至少一个 0,也就是说,不可逆矩阵。
对于一些 “好” 的系数矩阵(可逆矩阵) 来说,我们可以使用消元法来求解方程 ,我们还是从一个例子谈起。
我们仍然使用矩阵计算,将方程写为矩阵形式 。如下:
所谓矩阵的消元法,其实与我们在初等数学中学习的解二元一次方程组的消元法同理,都是通过将不同行的方程进行消元运算来简化方程,最后能得到简化的方程组。只不过这里我们把系数单独抽出来进行运算,寻找一种 U矩阵 (U upper triangular 上三角矩阵).
消元针对对象是系数矩阵AAA
首先注意,左上角的1是消元法的关键,我们称之为主元(pivot),接下来我们通过将第一行乘以倍数加到另一行,将第一列除了主元之外的元素全变为0。
注:
并不是所有的 A 矩阵都可消元处理,需要注意在我们消元过程中,
如果主元位置(左上角)为 0,那么意味着这个主元不可取,需要进行 “换行” 处理:
首先看它的下一行对应位置是不是 0,如果不是,就将这两行位置互换,将非零数视为主元。
如果是,就再看下下行,以此类推。若其下面每一行都看到了,仍然没有非零数的话,那就意味着这个矩阵不可逆,
消元法求出的解不唯一。
下面是 3 个例子:
2.2、回带求解
其实回带求解应该和消元法同时进行,只不过在我们讲解的时候以及在一些软件工作原理中它们是先后进行的,所以我们这里分开讨论,下面我们首先介绍—— 增广矩阵。
仍然是上面例一中我们给出的方程,
,我们接下来首先给出 增广矩阵 形式:
可以一下就看出来,增广矩阵 就是把 系数矩阵 A 和 向量 b 拼接成一个矩阵就行了。
然后像我们之前的消元法,但这次要带着增广矩阵部分一起进行:
再将上面的式子带回方程
从上向下开始求解,很容易求出 x, y, z 的值了。
3、消元矩阵
3.1、行向量与矩阵乘法
上面的消元法是从简单的变换角度介绍了消元的具体操作,接下来我们需要用矩阵来表示变换的步骤,这也十分有必要,因为这是一种 “系统地” 变换矩阵的方法。
矩阵与列向量的乘法,例如:


这并不能解决我们现在的问题,这是矩阵列的线性组合,因为消元法用到的是行变换,那么行向量和矩阵相乘呢?


3.2、消元矩阵介绍
学会了行向量与矩阵之间的乘法,我们就可以使用行向量对矩阵的行做操作了。所谓消元矩阵,就是将消元过程中的行变换转化为矩阵之间的乘法形式。
首先
把构成一个矩阵我们很容易验证这样的矩阵与其他的矩阵相乘不改变矩阵。消元矩阵就是它的变形形式,以上例矩阵说明:
如果:
我们消元过程是将第一行乘以-3加到第二行,这是对第二行的操作,那就从单位矩阵的第二行着手:
单独抽取第二行

这一步消元矩阵就是
记作,就是将矩阵A的第2行第1列的位置变为0的消元矩阵。
同样
记作那么上三角矩阵
设为,那么就是整个消元过程的消元矩阵
核心:求消元矩阵就是从单位阵入手,按照每次变换的消元步骤操作矩阵,能分别得到某行某列,最后累积得到即可。
3.3.1、行变换和列变换
受上面的消元矩阵的启发,交换矩阵中两行:
而交换矩阵中两列:
所以,左乘行交换,右乘列交换
3.3.2、逆矩阵初探
可以说学会了消元矩阵,就相当于可以用矩阵乘法对一个矩阵进行任何变化了,那么考虑一个反过程,即把一个消元结束的 矩阵 U 如何变为 未经消元的 矩阵 A 呢?
答案就是 乘上一个逆矩阵。
上题中的是第一行加到第二行,即那么与之相反,我们在第二行上加上第一行就可以复原这一运算过程,即:
此时的称为,,就是的逆矩阵。文章来源:https://www.toymoban.com/news/detail-412187.html
4、小结
这一个章节,我们从矩阵消元的角度,介绍解方程的通用做法,并介绍了消元矩阵,使我们从矩阵乘法层面理解了消元的过程,并延伸了消元矩阵的应用: 就是基于单位阵的变化,对矩阵进行行列变换的过程。文章来源地址https://www.toymoban.com/news/detail-412187.html
到了这里,关于矩阵消元法的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!