Fama-French 三因子模型-Toy模板网

这篇具有很好参考价值的文章主要介绍了Fama-French 三因子模型。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

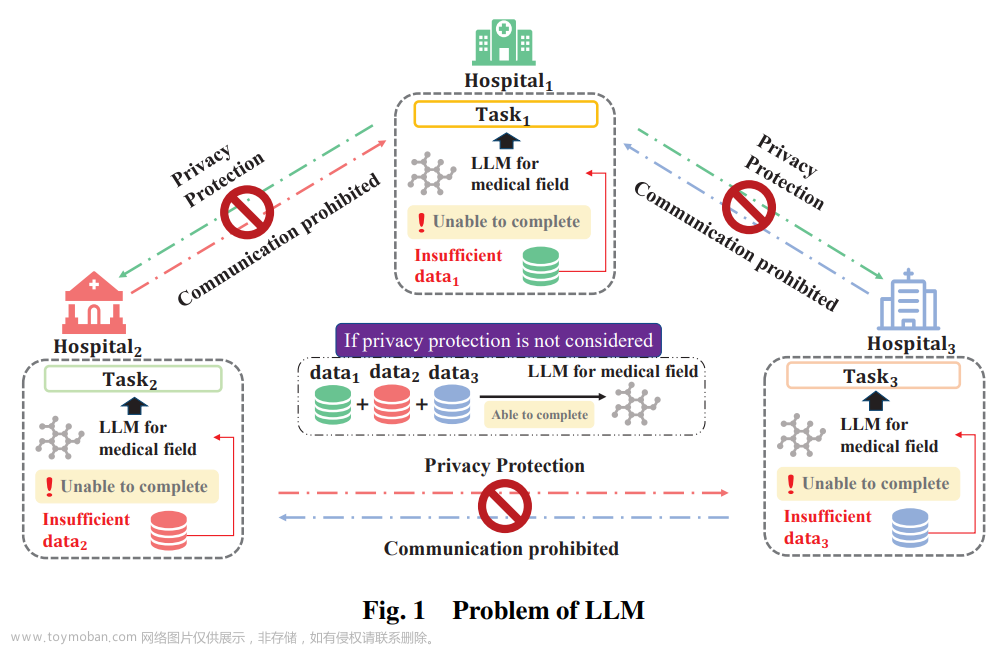
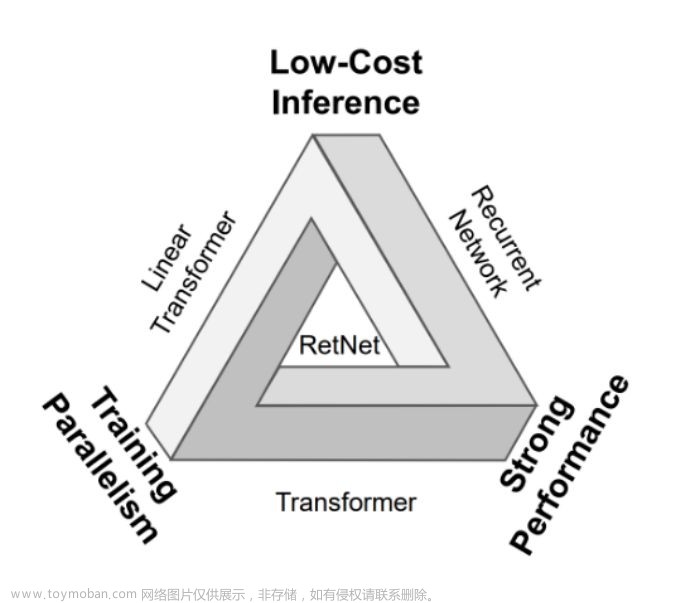
概述

自提出CAPM模型以后，不断有学者对其进行实证验证和应用。有证据表明，市场风险溢酬因子不能充分解释个别风险资产的收益率，因此学者们不断探寻影响资产定价的其它因子。

Fama和French于1992年7月和1993年8月对美国股票市场中股票收益的决定因素进行了全面性的研究分析，从可以解释股票收益率的众多因素中提取出3个重要的影响因子，即市场风险溢酬因子、市值因子和账面市值比因子，依照CAPM模型用这3个因子建立起线性模型来解释股票的收益率，这就是三因子模型。

其因子说明如下：

• 市场风险溢酬因子：对应市场投资组合的收益率

• 市值因子：对应的做多市值较小公司、做空市值较大公司的投资组合之收益率

• 账面市值比因子：对应的是做多高 B/M 比公司、做空低 B/M 比公司的投资组合之收益率。

其中：

B/M：账面市值比

BM=股东权益/公司市值.
股东权益(净资产)=资产总额-负债总额 (每股净资产x流通股数)
公司市值=流通股数x每股股价
账面市值比(BM)=股东权益/公司市值=(每股净资产x流通股数)/(流通股数x每股股价)=每股净资产/每股股价=B/P=市净率的倒数

应用

在实证中，我们常用：

来做回归检验，公式中

为超额收益率。在进行实证研究应用时，投资组合（或个股）收益率Rit、无风险收益率Rft、市场投资组合Rmt、市值因子组合SMBt和账面市值比因子组合HMLt的数据都是已知的，通过线性回归拟合最小化残差平方和我们可以得到参数

、

的估计值检验超额收益及3个因子的系数是否显著地异于0，也就是检验3个因子是否能够解释收益率。

Rit和Rmt的数值获取：国泰安数据库、中国证券市场交易数据CSMAR等有提供股票交易及收益率数据，市场投资组合收益率Rmt可以直接从数据库中苑；若研究对象为投资组合，Rit需要用个股收益率经过加权平均计算，加权平均有两种试：一种是等比例加权平均、另一种是按市值比例加权平均。

Rft的数值获取：无风险利率Rft可以取值为中国人民银行公布的人民币利率，也可以参考政府债券的利率。投资组合（或个股）i的风险溢酬 Rit-Rft和市场风险溢酬Rmt-Rft即可计算出。

模型代码实现：

以华夏银行股票（600015.SH）为例，获取2014年1月至2015年4月的数据，利用三因子模型计算影响其收益率受到哪方面影响比较大。

第一步：先计算华夏银行股票的各期收益率：

import ffn

import tushare as ts

import pandas as pd

import project_conf

import matplotlib

matplotlib.use('TkAgg')

import matplotlib.pyplot as plt

#----数据准备

pro = ts.pro_api(project_conf.tushare_token)

formStart ="20140101"

formEnd ="20150414"

#获取（600015.SH）华夏银行股票

stock_code='600015.SH'

#从公共配置文件中获取tushare的Key并且初始化pro对象

pro = ts.pro_api(project_conf.tushare_token)

#--------获取股票数据

df_hx= pro.daily(ts_code=stock_code, start_date=formStart, end_date=formEnd)

# #将日期列转换成日期格式并设置为索引

df_hx.index=pd.to_datetime(df_hx['trade_date'])

#将数据按正序排序

df_hx.sort_index(ascending=True,inplace=True)

#计算收益率

df_hx_return=ffn.to_returns(df_hx['close'])

df_hx_return.name='return'

df_hx_return.dropna(inplace=True)

运行结果：

第二步：载入三因子数据，并与第一步计算的收益率合并成一张表格

#获取三因子(文件中是已经计算好的三因子，见附件)

three_factors=pd.read_table('datafile/ThreeFactors.txt',index_col='TradingDate')

#设置日期作为索引

three_factors.index=pd.to_datetime(three_factors.index)

#截取2014年1月2日以后的数据

three_factors_2014=three_factors.query('index>"2014-01-02"')

#获取三个因子变量(其中，标1的是用流通市值加权平均计算的，标2的是用总市值加权平均计算的这里取标2的

df_tf=three_factors_2014[['RiskPremium2','SMB2','HML2']]

df_data=pd.merge(df_hx_return,df_tf,left_index=True,right_index=True)

print(df_data.head())

运行结果：

第三步：制作散点图，分析华夏收益率分别与三个因子之间的相关性

#开始作图分析相关性

plt.subplot(2,2,1)

plt.scatter(df_data['return'],df_data['RiskPremium2'])

plt.subplot(2,2,2)

plt.scatter(df_data['return'],df_data['SMB2'])

plt.subplot(2,2,3)

plt.scatter(df_data['return'],df_data['HML2'])

plt.show()

运行结果：

从图可以看到，其收益率与三个因子都是高度相关的。

第四步：训练线性回归模型，输出参数

#开始训练模型

import statsmodels.api as sm

reg_three_facter=sm.OLS(df_data['return'],sm.add_constant(df_data.iloc[:,1:4]))

res=reg_three_facter.fit()

print(res.summary())

#提取模型参数

print("模型输出参数为")

print(res.params)

运行结果：

Summary输出的结果：

提取的参数：

模型输出参数为

const 0.000166

RiskPremium2 1.046047

SMB2 0.246412

HML2 0.509862

dtype: float64

结论：

综合上述模型的输出结果，可以看到，三个因子对华夏银行股价均有不同程度的影响，其中RiskPremium2（即市场风险溢酬）对其股价影响最大，说明华夏银行自身经营较稳健，价格受自身波动影响不明显，而受市场、行业影响较大。文章来源地址https://www.toymoban.com/news/detail-412408.html

到了这里，关于Fama-French 三因子模型的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！