线性回归（线性拟合）与非线性回归(非线性拟合)原理、推导与算法实现（一）-Toy模板网

这篇具有很好参考价值的文章主要介绍了线性回归（线性拟合）与非线性回归(非线性拟合)原理、推导与算法实现（一）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

关于回归和拟合，从它们的求解过程以及结果来看，两者似乎没有太大差别，事实也的确如此。从本质上说，回归属于数理统计问题，研究解释变量与响应变量之间的关系以及相关性等问题。而拟合是把平面的一系列点，用一条光滑曲线连接起来，并且让更多的点在曲线上或曲线附近。更确切的说，拟合是回归用到的一种数学方法，而拟合与回归的应用场合不同。拟合常用的方法有最小二乘法、梯度下降法、高斯牛顿（即迭代最小二乘）、列-马算法。其中最最常用的就是最小二乘法。并且拟合可以分为线性拟合与非线性拟合，非线性拟合比较常用的是多项式拟合。根据自变量的个数，拟合也可以分为曲线拟合与曲面拟合等。

而回归大多数采用最小二乘法。回归可以分为一元线性回归、一元非线性回归、多元线性回归、多元非线性回归等。

通常情况下，拟合通常所处理的是一元函数（即曲线拟合），求自变量与因变量之间的关系；对于多元回归问题，一般会涉及很多个解释变量。通常情况下，我们会把线性回归与线性拟合定义等同。本文对于回归问题，与拟合方法结合，讲解对于不同情况下拟合方程的求法，对相关系数等知识不做展开。

一：最小二乘法。

无论是在高等数学、线性代数，还是数理统计，我们都可以看到最小二乘法的身影。只不过每一部分侧重点不同，最终是殊途同归的。但是兔兔建议用矩阵的方法来做，这样很便于理解，计算起来也很方便。

最小二乘法的基本思路是：确定函数f(x),使得各个点x1,x2..xn处的函数值偏差f(x1)-y1、f(x2)-y2...f(xn)-yn的平方和或绝对值和最小。如果是一元线性拟合（回归），我们可以设方程为f(x)=ax+b。

这时我们求得函数值偏差平方和为 $线性回归（线性拟合）与非线性回归(非线性拟合)原理、推导与算法实现（一）$ 。为了求它的最小值，利用高数的方法，就可以使M分别对a和b的偏导为0，最终求解得方程组：

$线性回归（线性拟合）与非线性回归(非线性拟合)原理、推导与算法实现（一）$

把方程组解出来得a,b就得出拟合结果了。这个式子也就是我们在数理统计中一元回归方程中常用的式子之一，不过比较麻烦。当自变量（解释变量）的个数是多个时，我们设方程为 $线性回归（线性拟合）与非线性回归(非线性拟合)原理、推导与算法实现（一）$ ，或者是多项式拟合，设函数为 $线性回归（线性拟合）与非线性回归(非线性拟合)原理、推导与算法实现（一）$ 。这样逐个求偏导就麻烦很多。

这个时候矩阵的方法就使得拟合结果十分简洁。而且可以发现，如果用矩阵进行一元线性拟合，展开后和上面那个结果是一致的。

例如对于多元线性回归（二元时也可以看作是平面拟合），我们设每组数据有p个指标，一共有n组数据，在多元统计中，我们称：

为样本数据矩阵（观测阵）。如果我们设方程为 $线性回归（线性拟合）与非线性回归(非线性拟合)原理、推导与算法实现（一）$ ，把每一组数据带入，求偏导等于0 时各个a的值。这个推导过程比较麻烦。不过，如果我们对于这个式子，定义X、Y、a为：

$线性回归（线性拟合）与非线性回归(非线性拟合)原理、推导与算法实现（一）$

这样等式就是。之后就是

这样，我们就很容易得到a了，虽然不是严格的证明，但是推算和应用却十分的简便！严格的矩阵求导证明方法兔兔写在下面了，感兴趣的同学可以看一下。（关于矩阵求导可以看兔兔的另一篇《矩阵求导（本质、原理与推导）详解》）

线性回归（线性拟合）与非线性回归(非线性拟合)原理、推导与算法实现（一）

那么，一元多项式拟合也是如此。如果设方程为 $线性回归（线性拟合）与非线性回归(非线性拟合)原理、推导与算法实现（一）$ 。定义X,Y,a为：

$线性回归（线性拟合）与非线性回归(非线性拟合)原理、推导与算法实现（一）$

这样等式就是Xa=Y,解法与推导与以上过程一样，结果为：。

对于多元非线性回归（拟合），也可以设多元多项式形式，拟合出多元多项式函数。

算法实现：

（1）二元线性回归：

对表格的数据做二元线性回归。

指标x1	7	1	11	7	11	3	8	9	2
指标x2	26	29	56	31	52	55	71	31	54
y	93	91	190	108	177	172	231	111	167

代码实现：

import numpy as np
x1=[7,1,11,7,11,3,8,9,2]
x2=[26,29,56,31,52,55,71,31,54]
y=[93,91,190,108,177,172,231,111,167]
X=np.mat([[1 for i in range(len(x1))],x1,x2]).T #把样本转成X
Y=np.mat(y).T #把y转成Y
a=np.linalg.inv(X.T*X)*X.T*Y #求a的公式
a0=a[0,0];a1=a[1,0];a2=a[2,0]
ax=plt.axes(projection='3d')
xx=np.arange(2,12,0.1)
yy=np.arange(20,75,0.5)
XX,YY=np.meshgrid(xx,yy)
Z=a0+a1*XX+a2*YY #平面方程
ax.scatter(x1,x2,y,color="red") #画散点
ax.plot_surface(XX,YY,Z,cmap="winter") #画拟合平面
plt.show()

散点图如下：

线性回归（线性拟合）与非线性回归(非线性拟合)原理、推导与算法实现（一）

拟合平面图：

线性回归（线性拟合）与非线性回归(非线性拟合)原理、推导与算法实现（一）

我们发现，大部分点都落在平面附近。

（2）一元多项式回归

可以对表格的数据做三次多项式拟合。

x	1	2	4	5	6	7	10	11	13
y	18	20	0	-10	-12	0	180	308	702

import numpy as np
x=[1,2,4,5,6,7,10,11,13]
y=[18,20,0,-10,-12,0,180,308,702]
def to_X(x,n):
    '''把数据X转成矩阵X，n是拟合多项式的次数'''
    l=[]
    for i in x:
        s=[]
        for j in range(n+1):
            s.append(i**j)
        l.append(s)
    return np.mat(l)
Y=np.mat(y).T
X=to_X(x=x,n=3) #做三次多项式拟合
a=np.linalg.inv(X.T*X)*X.T*Y
xx=np.arange(0,14,0.1)
yy=a[0,0]+a[1,0]*xx+a[2,0]*xx**2+a[3,0]*xx**3
plt.scatter(x,y,color="red") #画散点图
plt.plot(xx,yy) #拟合曲线
plt.show()

散点图与拟合曲线图如下所示：

线性回归（线性拟合）与非线性回归(非线性拟合)原理、推导与算法实现（一）

我们发现，用三次多项式拟合，效果比较好。至于其它的多项式同学们也可以尝试以下，但需要注意的是：有时不一定多项式次数越多，拟合效果越好。

（3）二元多项式拟合（曲面拟合）

对于曲面拟合情况，我们可以和曲线拟合，分为n次多项式拟合。如果假设是二次曲面，就是 $线性回归（线性拟合）与非线性回归(非线性拟合)原理、推导与算法实现（一）$ 。三次曲面： $线性回归（线性拟合）与非线性回归(非线性拟合)原理、推导与算法实现（一）$

计算方法仍是把数据转换成矩阵X，代入公式。我们对下面数据做二次曲面拟合。

x1	1	-2	6	3	4	-4	-2	3	10
x2	2	9	-4	3	6	-3	2	2	-4
y	9	49	4	80	101	50	0	25	6

import numpy as np
x1=[1,-2,6,3,4,-4,-2,3,10]
x2=[2,9,-4,3,6,-3,2,2,-4]
y=[9,49,4,80,101,50,0,25,6]
def to_X(x1,x2):
    n=len(x1)
    X=[[1 for i in range(n)],
       [i**2 for i in x1],
       [j**2 for j in x2],
       [i*j for i,j in zip(x1,x2)]]
    return np.mat(X).T
X=to_X(x1,x2)
Y=np.mat(y).T
a=np.linalg.inv(X.T*X)*X.T*Y
a0=a[0,0];a1=a[1,0];a2=a[2,0];a3=a[3,0]
ax=plt.axes(projection='3d') #画散点图
ax.scatter(x1,x2,y,color='red')
xt=np.arange(-5,10)
yt=np.arange(-5,10)
Xt,Yt=np.meshgrid(xt,yt)
Z=a0+a1*Xt**2+a2*Yt**2+a3*Xt*Yt
ax.plot_surface(Xt,Yt,Z) #画拟合曲面
plt.show()

运行结果如下图所示。

线性回归（线性拟合）与非线性回归(非线性拟合)原理、推导与算法实现（一）

二：梯度下降法

关于梯度下降法，兔兔在《梯度下降法（Gradient descant）算法详解》一文已经讲过。在这里，我们先设函数f(x),然后求损失函数取最小值时的a的值（这里用二分之一是为了方便，求导后乘以2后化为1）。如果用矩阵表示,可以是。为了使损失函数最小，可以用梯度下降的方法并求得a值。关于矩阵的导数兔兔在上面的矩阵求导过程中已经写过，这里就不再重复了。

算法实现

x	1	3	5	7	9
y	3	5	7	8	12

import numpy as np
x=[1,3,5,7,9]
y=[3,5,7,8,12]
X=np.mat([[1 for i in range(5)],x]).T
Y=np.mat(y).T
def Grand_descend(x,y,circle=100,alpha=0.001):
    '''梯度下降'''
    a=np.random.normal(size=(2,1)) #初始化a
    for i in range(circle): #迭代次数
        a-= alpha*(X.T*X*a-X.T*Y) #批量梯度下降
    return a
a=Grand_descend(x=X,y=Y)
xt=np.arange(0,10)
yt=a[0,0]+a[1,0]*xt
plt.scatter(x,y,color='red')
plt.plot(xt,yt,color='green')
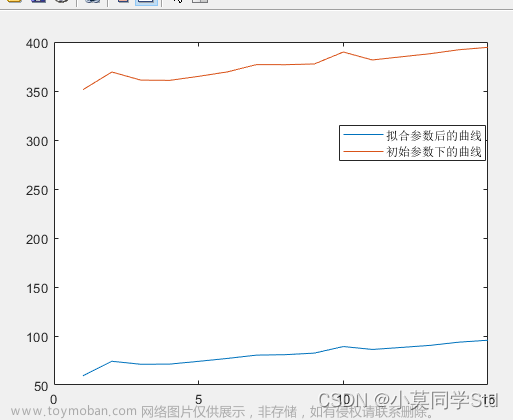
plt.show()

结果如下：

线性回归（线性拟合）与非线性回归(非线性拟合)原理、推导与算法实现（一）

这里学习率需要小一些，否则容易出现梯度爆炸。迭代次数也需要适当。对于前面最小二乘法的三个例子，同样可以用梯度下降这种方法来进行拟合计算。

三：总结

关于回归（拟合）问题，本文先介绍了最小二乘法与梯度下降法，二者在公式推导上有很多相似的地方，目的都是在确定函数形式后，求损失函数的最小值时的参数。关于线性拟合问题，相对容易一些，而对于非线性的问题，往往还要因具体情况而分析，选特定的方法，兔兔之后会单独讲解。关于高斯牛顿与列-马算法，二者也有许多相似之处，兔兔将会在第二部分进行讲解。文章来源地址https://www.toymoban.com/news/detail-412718.html

到了这里，关于线性回归（线性拟合）与非线性回归(非线性拟合)原理、推导与算法实现（一）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！