01背包问题——以小明的背包1 为例-Toy模板网

这篇具有很好参考价值的文章主要介绍了01背包问题——以小明的背包1 为例。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

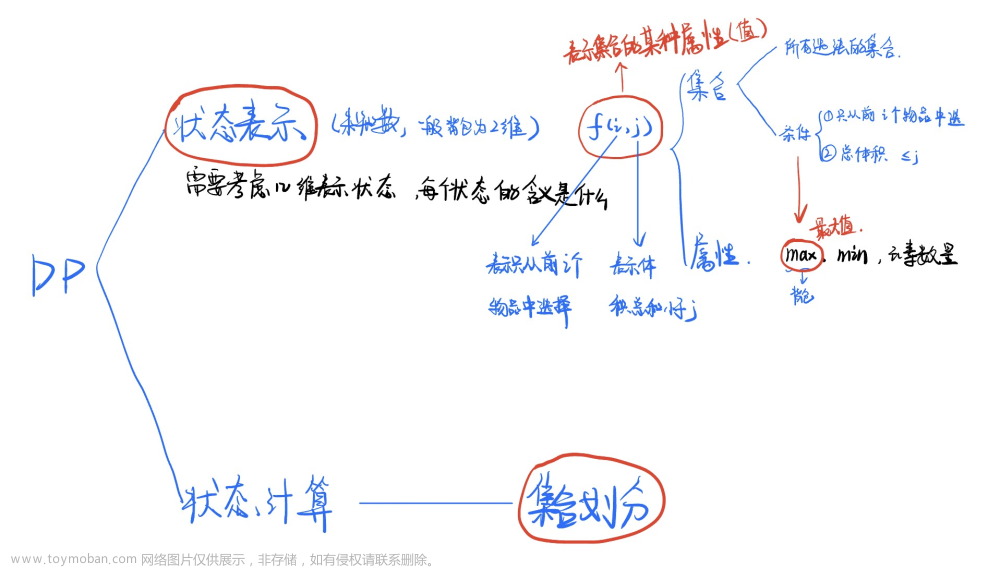
本文旨在加强01背包问题的记忆与理解，步骤会细化

问题如下：

小明有一个容量为 VV的背包。

这天他去商场购物，商场一共有 N 件物品，第 i 件物品的体积为 w ，价值为 v 。

小明想知道在购买的物品总体积不超过 V 的情况下所能获得的最大价值为多少，请你帮他算算。

输入描述
输入第 1 行包含两个正整数 N,V，表示商场物品的数量和小明的背包容量。

第 2∼N+1 行包含 2 个正整数 w,v，表示物品的体积和价值。

输入如下：

下面直接给出题解代码

#include <iostream>
using namespace std;
int dp[105][3005];
struct good{
  int v;
  int w;
}a[105];
int main()
{
  	int n,v;
  	cin>>n>>v;
  	for(int i=1;i<=n;i++)
 	{
    	cin>>a[i].w>>a[i].v;
	}
 	for(int i=1;i<=n;i++)
	{
    	for(int j=1;j<=v;j++)
   		{
     		if(j<a[i].w)
     		dp[i][j]=dp[i-1][j];
     		else
     		dp[i][j]=max(dp[i-1][j-a[i].w]+a[i].v,dp[i-1][j]);
 		}
	}
	cout<<dp[n][v];
  return 0;
}

该题是01背包问题的基础题。
下面给出样例输入对应的dp值：
01背包问题——以小明的背包1 为例

分析：

对于一个物品而言，有两种选择（0 1 的体现），要么装进背包，要么，不装进背包。那么对于无限空间下的情况就有 2^n-1 种。显然难以完全计算并判断。而动态规划则很好的解决了这个问题。
下面分为两种情况：

一、该物品可装。可装的话，需要对应 w 的空间，假设装完之后正好达到满空间，则应该是 dp[i][j]=dp[i-1][j-w]+v; 可见该处的值由 i-1 行的dp决定，即完成了前面几个物品装与不装的判断后给出的答案。要想装入该物品必然需要满足该物品空间的前驱点。

二、该物品不装。不装有可分成两种情况。有可能是空间不满足，无法装入，所以不装。也有可能是因为装入之后占用了空间，反而挤出了前面判读过最优值情况下的物品，使得值反而变小。那么这个最优值在哪呢？很显然，当背包空间相同的时候，最优值就是 i-1 行对应相同背包容量的解。判断两者哪个更加合理即可。

优化代码：
利用滚动数组节省空间，代码如下：文章来源地址https://www.toymoban.com/news/detail-412743.html

#include <iostream>
using namespace std;
int dp[3005];
int main()
{
  int n,v;
  cin>>n>>v;
  for(int i=1;i<=n;i++)
  {
  	cin>>w>>v>>s;
  	for(int j=v;j>=0;j--)//一定要从j值大出开始，否则会影响后续滚动
  	{
  		dp[j]=max(dp[j],dp[j-w]+v);	
  	}
  }
  cout<<dp[v];
  return 0;
}