C语言-实现顺序二叉树和平衡二叉树AVL-Toy模板网

这篇具有很好参考价值的文章主要介绍了C语言-实现顺序二叉树和平衡二叉树AVL。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

1. 结构体

在实现二叉树之前先看下结构体的一些使用方法

数组是保存一系列相同的数据。在实际问题中，一组数据往往有很多种不同的数据类型。例如，登记学生的信息，可能需要用到 char型的姓名，int型或 char型的学号，int型的年龄

///第一种方式
struct Person{
    int age;
    char name[20];
};
//之后定义变量
struct Person a, b;
 
///第二种方式（声明的同时定义）
struct Person {
    int age;
    char name[20];
}a, b;
 
///第三种方式（不需要提供结构体名字，直接定义）
struct {
    int age;
    char name[20];
}a, b;

访问结构成员

访问其中的各个元素，用结构成员运算符点（.）。即访问成员的一般形式是：结构变量名 . 成员名
如 a.name 表示学生 a 的姓名。

结构成员的初始化

1）结构体的成员逐个赋值

struct Person stu1;      //定义结构体变量
strcpy(stu1.name, "Jack");
stu1.age= 18;

2）整体赋值

struct Person stu1 = {"jack", 12};

也可以在初始化的时候赋值

struct Person {                 //声明结构体 Person
    char name[20];               
    int age;                   
}stu = {"Mike", 20};        //注意初始化值的类型和顺序要与结构体声明时成员的类型和顺序一致

也可以按照任意的顺序使用指定初始化：

struct Person st = { .name = "Smith",
                          .age= 18 };

3）整体拷贝

struct Person stu1 = {"jack_mike", 12};
struct Person stu2;
stu2 = stu1;

如上每次使用结构体均需要写struct，可以使用typedef 简化书写

typedef struct Person {
    char name[20];
    int age;
}Person;
// 定义一个结构体
    Person stu1 = {"jack", 12};

结构成员指针

结构变量作为函数的参数传递时，将整个结构体变量拷贝为副本，传送的空间开销比较大，特别是当成员有数组的时候，程序效率较低。所以可以考虑使用结构体指针。

通过结构指针间接访问成员值:

访问的一般形式：
（*结构指针变量）. 成员名或结构指针变量 -> 成员名

typedef struct Person {
    char name[20];
    int age;
}Person;

int main(){
    Person stu1 = {"jack", 12};
    Person* stuP = &stu1;
// (*stuP).name
    printf("Person name: %s \n", (*stuP).name);
//  stuP->name
    printf("Person name: %s \n", stuP->name);

    return 0;
}

2. 二叉树

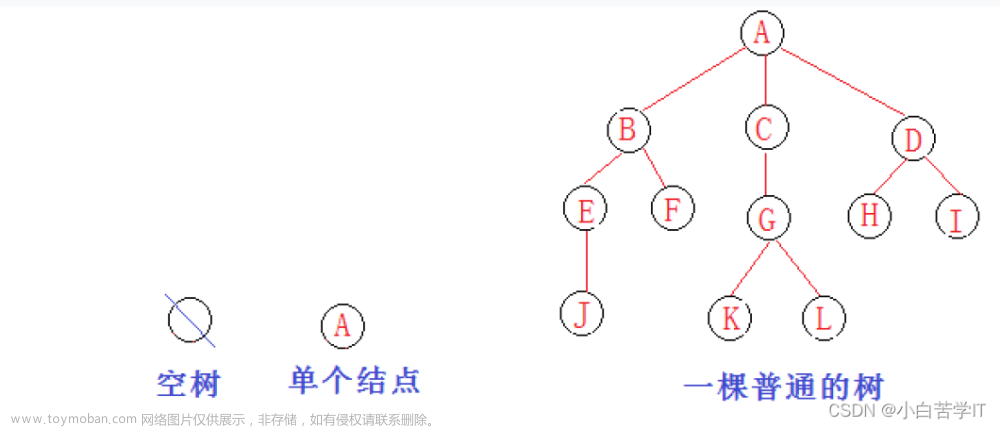
2-1）树的基本概念

C语言-实现顺序二叉树和平衡二叉树AVL

节点的度：一个节点含有的子树的个数称为该节点的度；如上图：A的为6
叶节点或终端节点：度为0的节点称为叶节点；如上图：B、C、H、I…等节点为叶节点
非终端节点或分支节点：度不为0的节点；如上图：D、E、F、G…等节点为分支节点
双亲节点或父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点；如上图：A是B的父节点
孩子节点或子节点：一个节点含有的子树的根节点称为该节点的子节点；如上图：B是A的孩子节点
兄弟节点：具有相同父节点的节点互称为兄弟节点；如上图：B、C是兄弟节点
树的度：一棵树中，最大的节点的度称为树的度；如上图：树的度为6
节点的层次：从根开始定义起，根为第1层，根的子节点为第2层，以此类推；
树的高度或深度：树中节点的最大层次；如上图：树的高度为4
堂兄弟节点：双亲在同一层的节点互为堂兄弟；如上图：H、I互为兄弟节点
节点的祖先：从根到该节点所经分支上的所有节点；如上图：A是所有节点的祖先
子孙：以某节点为根的子树中任一节点都称为该节点的子孙。如上图：所有节点都是A的子孙
森林：由m（m>0）棵互不相交的树的集合称为森林；

二叉树

C语言-实现顺序二叉树和平衡二叉树AVL

二叉树是由一个根节点加上两棵别称为左子树和右子树的二叉树组成；二叉树不存在度大于2的结点

2-2）二叉树的创建与递归遍历

C语言-实现顺序二叉树和平衡二叉树AVL

依据前序遍历建二叉树，树结构如上图所示：

参数是二级指针时，需要传入左节点的地址，需要改变指针的指向

#include <stdio.h>
#include <stdlib.h>
 
typedef struct treeNode{
    struct treeNode* left;
    struct treeNode* right;
    char data;
}treeNode;
 
treeNode* mallocTreeNode(char data){
    treeNode* node = (treeNode*)malloc(sizeof(treeNode));
    node->data = data;
    return node;
}
 
// 使用递归的方法创建一棵二叉树，不用return 这里使用二级指针
void createTree(treeNode** node, char* src, int* index){
    char ch = *(src + *index);
    (*index)++;
    printf("ch is %c \n", ch);
    if (ch != '#'){
        // 根左右，前序遍历二叉树
        *node = mallocTreeNode(ch);
        createTree(&((*node)->left), src, index);
        createTree(&((*node)->right), src, index);
    }else{
        *node = NULL;
    }
}
 
treeNode* createTree2(char* src, int* index){
    char ch = *(src + *index);
    (*index)++;
    printf("ch is %c \n", ch);
    if (ch != '#'){
        // 根左右，前序遍历二叉树
        treeNode* node = mallocTreeNode(ch);
        node->left = createTree2(src, index);
        node->right = createTree2(src, index);
        return node;
    }
    return NULL;
}

main 函数

int main(){
    printf("this is binary tree test =====\n");
    char* src = "ABD##E##C##";
    // Node* root = create_tree();
    treeNode* root = NULL;
    int index = 0;
    // createTree(&root, src, &index);
    root = createTree2(src, &index);
    printf("root left= %c \n", root->left->data);
 
    return 0;
}

递归遍历二叉树：前序遍历、中序遍历、后续遍历

// 前序遍历二叉树: 中左右
void printPreOrderTree(treeNode* root){
    if (root != NULL){
        printf(" %c - ", root->data);
        printPreOrderTree(root->left);
        printPreOrderTree(root->right);
    } 
}
 
// 中序遍历二叉树: 左中右
void printInOrderTree(treeNode* root){
    if (root != NULL){
        printInOrderTree(root->left);
        printf(" %c - ", root->data);
        printInOrderTree(root->right);
    } 
}
 
// 后序遍历二叉树: 左右中
void printBackOrderTree(treeNode* root){
    if (root != NULL){
        printBackOrderTree(root->left);
        printBackOrderTree(root->right);
        printf(" %c - ", root->data);
    } 
}

二叉树的非递归遍历可以看这篇博文

5-3）顺序二叉树

顺序二叉树的中序遍历是有顺序的。

#include <stdio.h>
#include <stdlib.h>
 
typedef struct treeNode{
    struct treeNode* left;
    struct treeNode* right;
    int data;
}treeNode;
 
treeNode* mallocTreeNode(int data){
    treeNode* node = (treeNode*)malloc(sizeof(treeNode));
    node->data = data;
    return node;
}
 
// 中序遍历二叉树: 左中右
void printInOrderTree(treeNode* root){
    if (root != NULL){
        printInOrderTree(root->left);
        printf(" %d - ", root->data);
        printInOrderTree(root->right);
    } 
}
 
// 由于需要改变头部节点的值 // -> 运算符优先级比 & 大
void orderedTreeInsert(treeNode** node, int data){
    if(*node == NULL){
        *node = mallocTreeNode(data);
        (*node)->left = NULL;
        (*node)->right = NULL;
    }else if (data > (*node)->data ){
        
        orderedTreeInsert(&(*node)->right, data);
    }else if(data < (*node)->data){
        orderedTreeInsert(&(*node)->left, data);
    }else{
        // 如果2 个值相等，则不插入，忽略
        return;
    }
}
 
// 需要找到最底层的 node 先free，然后一直往上递归。类似于后序遍历。左右根
void freeNode(treeNode** node){
    if (*node != NULL){
        freeNode(&(*node)->left);
        freeNode(&(*node)->right);
        printf("free node: %d \n", (*node)->data);
        free(*node);
        *node = NULL;
    }
}
 
int main(){
    printf("this is ordered tree == \n");
    const int SIZE = 7;
    int data[7] = {4, 6, 3, 7, 2, 9, 1};
    treeNode* root = NULL;
    for (int i=0; i< SIZE; i++){
        orderedTreeInsert(&root, data[i]);
    }
    printInOrderTree(root);
    printf("\n");
    freeNode(&root);
 
    return 0;
}

main函数创建顺序二叉树

int main(){
    int data[7] = {4, 6, 3, 7, 2, 9, 1};
    int size= sizeof(data) / sizeof(int);
    treeNode* root = NULL;
    for (int i=0; i< size; i++){
        orderedTreeInsert(&root, data[i]);
    }
    printInOrderTree(root);
    printf("\n");
    freeNode(&root);
 
    return 0;
}

5-4）二叉平衡树 AVL 树

二叉排序树可以在一定程度上提高查找（搜索）的效率，但仍然会出现特殊情况，让二叉排序树失效。例如，将序列{1,2,3,4,5,6, 7}中的元素依次插入到二叉排序树中，会得到右斜树，这就相当于一个单链表了，搜索效率降低为O(n)。

C语言-实现顺序二叉树和平衡二叉树AVL

上述的二叉排序树输出的中序遍历和后续遍历的值为如下，可以看出退化成了一个链表了。

1 -  2 -  3 -  4 -  5 -  6 -  7 - 
back print 
 7 -  6 -  5 -  4 -  3 -  2 -  1 -

平衡二叉树的性质：
C语言-实现顺序二叉树和平衡二叉树AVL

可以是空树。

假如不是空树，任何⼀个结点的左子树与右子树都是平衡⼆叉树，并且 高度之差的绝对值不超过 1 。

二叉平衡树的构建

首先判断当前节点的值与插入的节点值的大小，递归插入到左、右节点中
如果是插入到右节点，先判断左右子树是否是平衡的，如果不平衡的话，则判断如下：

-1）如果当前插入的值大于节点的右节点值的话，则表示是 RR形式的，需要左旋
-2）如果当前插入的值小于节点的右节点值的话，则表示是 RL 形式的，先对当前节点的右节点进行右旋，更新节点，再对根部节点左旋。

如果是插入到左节点，先判断左右子树是否是平衡的，如果不平衡的话，则判断如下：

-1）如果当前插入的值小于节点的左节点值的话，则表示是 LL 形式的，需要右旋
-2）如果当前插入的值大于于节点的左节点值的话，则表示是 LR 形式的，先对当前节点的左节点进行左旋，更新节点，再对根部节点右旋。

RR形式，左旋
C语言-实现顺序二叉树和平衡二叉树AVL


void RRrotation(treeNode* node, treeNode** root){
    // 缓存 tmp，因为tmp 会最终作为新的头部节点
    treeNode* tmp = node->right;
    node->right = tmp->left;
    tmp->left = node;
    // 更新tmp 和 node 的节点的高度
    node->height = MAX(getTreeHeight(node->left), getTreeHeight(node->right)) + 1;
    tmp->height = MAX(getTreeHeight(tmp->left), getTreeHeight(tmp->right)) + 1;
    // 更新根部节点
    *root = tmp;

LL形式，右旋
C语言-实现顺序二叉树和平衡二叉树AVL

void LLrotation(treeNode* node, treeNode** root){
    treeNode* tmp = node->left;
    node->left = tmp->right;
    tmp->right = node;
    node->height = MAX(getTreeHeight(node->left), getTreeHeight(node->right)) + 1;
    tmp->height = MAX(getTreeHeight(tmp->left), getTreeHeight(tmp->right)) + 1;
    // 更新根部节点
    *root = tmp;
}

右孩子的左子树 RL

右孩子的左子树插入导致失衡
C语言-实现顺序二叉树和平衡二叉树AVL

左孩子的右子树 LR

左孩子的右子树插入导致失衡

C语言-实现顺序二叉树和平衡二叉树AVL

#include <stdio.h>
#include <stdlib.h>
 
#define MAX(a, b) ((a > b) ? (a) : (b))
 
typedef struct treeNode{
    struct treeNode* left;
    struct treeNode* right;
    int height;
    int data;
}treeNode;
 
treeNode* mallocTreeNode(int data){
    treeNode* node = (treeNode*)malloc(sizeof(treeNode));
    node->data = data;
    node->height = 0;
    return node;
}
 
int getTreeHeight(treeNode* node){
    return node ? node->height : 0;
}
 
void avlTreeInsert(treeNode** node, int data){
    if (*node == NULL){
        *node = mallocTreeNode(data);
        (*node)->left = NULL;
        (*node)->right = NULL;
    }else if(data > (*node)->data){
        // 如果插入的节点要大于当前的节点,插入到右节点
        avlTreeInsert(&(*node)->right, data);
        // 再对节点进行旋转
        int leftHeight = getTreeHeight((*node)->left);
        int rightHeight = getTreeHeight((*node)->right);
        // 如果是左右子树是不平衡的树
        if (rightHeight-leftHeight == 2){
            // 如果当前节点还大于右边最大的节点，则进行左旋
            // 找到首个节点即可。
            if (data > (*node)->right->data){
                RRrotation(*node, node);
            }else{
                // RL 形式的树，先对node->right 节点右旋，然后对node 左旋
                RRrotation((*node)->right, &(*node)->right);
                LLrotation(*node, node);
            }
        }
    }else if(data < (*node)->data){
        avlTreeInsert(&(*node)->left, data);
        int leftHeight = getTreeHeight((*node)->left);
        int rightHeight = getTreeHeight((*node)->right); 
        if (leftHeight-rightHeight == 2){
            if (data < (*node)->left->data){
                // LL 形式节点
                LLrotation(*node, node);
            }else{
                // LR 形式的树，先对node->left 节点左旋，然后对更新后的node 节点右旋
                LLrotation((*node)->left, &(*node)->left);
                RRrotation(*node, node);
            }
        }       
    }else{
        return;
    }
    (*node)->height = MAX(getTreeHeight((*node)->left), getTreeHeight((*node)->right)) + 1;
}
 
void orderPrintTree(treeNode* root){
    if (root != NULL){
        // 中序遍历: 左根右
        orderPrintTree(root->left);
        printf(" -%d ", root->data);
        orderPrintTree(root->right);
    }
}
 
void printBackOrderTree(treeNode* root){
    if (root != NULL){
        printBackOrderTree(root->left);
        printBackOrderTree(root->right);
        printf(" %d - ", root->data);
    } 
}
 
 
int main(){
 
    int arr[] = {1, 2, 3, 4, 5, 6, 7};
    int size = sizeof(arr) / sizeof(int);
    treeNode* root = NULL;
    for (int i=0; i< size; i++){
        avlTreeInsert(&root, arr[i]);
    }
    orderPrintTree(root);
    printf("back order === \n");
    printBackOrderTree(root);
 
    return 0;
}

二叉平衡树的搜索的时间复杂度为 O(log2n)

二叉平衡树博客惨参考文章来源地址https://www.toymoban.com/news/detail-413049.html

到了这里，关于C语言-实现顺序二叉树和平衡二叉树AVL的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！