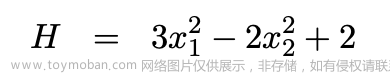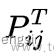有约束优化问题
第一篇文章讲述了,怎么从二次多项式获得QUBO,获得QUBO后,量子退火法就可以直接给你最优解(没有特殊说明的话,所有的变量都是0或1)。其实,实际问题一般都是有约束的,比如上篇的例题加上约束条件后。
这种带约束的优化问题,我们要求出满足约束条件下的令H值最小的,(x1,x2)的组合。没有约束的情况,(x1,x2)的组合和H的取值如下表,最优解为(x1,x2)=(0,1):
从上面的表中可以看到,因为需要满足约束条件,最优解变为(x1,x2)=(0,0)。这道例题变量比较少,可以很快找到满足约束条件的最优解。
其实,正常有约束的优化问题会变换成下面的形式,然后求解。
其中惩罚函数g()就是从约束条件获得。怎么把约束条件转化为惩罚函数呢?答案就是,把约束条件转化为对应的**【哈密顿算符(Hamiltonian) 】**
约束条件转换为【哈密顿算符H】
我们可以这么想,如果有一个二次多项式,让它取最小值的解,刚好是某个【哈密顿算符H】的最小值(H=0)的解。以上面的约束条件为例:
x
1
⩾
x
2
x1 \geqslant x2
x1⩾x2
那么满足约束条件的(x1, x2)有[ (0, 0), (1, 0), (1, 1) ]三个组合。逆向思维,这三个组合会是哪个【哈密顿算符H】的最小值的解呢?有兴趣的读者可以自己想一想,这里我直接给出答案。
上面H=0的解,就是满足约束条件的,(x1, x2)=[ (0, 0), (1, 0), (1, 1) ]。对应的QUBO矩阵就是。
这时候带有惩罚函数项的新的H变为:
很多读者到这里,就会有疑问,每次都要把二次多项式写成QUBO矩阵的话,很麻烦。能不能直接输入二项式呢?答案是,可以的。
Pyqubo:自动把二次多项式转换为QUBO
# neal是模拟退火的库
import neal
# pyqubo 可以使用Binary定义变量,Constarint定义约束
from pyqubo import Binary, Constraint
x1, x2 = Binary('x1'), Binary('x2')
# M是约束强度
M = 5.0
#定义哈密顿算符H
H = 3 * x1**2 - 2 * x2**2 + M * Constraint((x2 - x1*x2), label='x1>=x2')
model = H.compile()
# 无视offset就行了,QUBO用来做模拟退火的输入
qubo, offset = model.to_qubo()
sampler = neal.SimulatedAnnealingSampler()
raw_solution = sampler.sample_qubo(qubo)
raw_solution.first.sample
>>> {'x1': 0, 'x2': 0}
我们可以看到,最后的结果是(x1, x2)=(0, 0)。确实是最优解。但是M值(就是前面公式里的 λ \lambda λ)如果太小,可能得不到最优解。文章来源:https://www.toymoban.com/news/detail-413254.html
常见条件约束对应的H
前任栽树,后人乘凉,常见的约束条件对应的H如下表所示:
本文介绍了,如何添加约束条件到目标函数中,下篇讲一个经典的旅行商最短路径问题如何建模,求解。文章来源地址https://www.toymoban.com/news/detail-413254.html
到了这里,关于量子退火算法入门(2):有约束优化问题的QUBO怎么求?的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!