高斯滤波及其原理
一、高斯函数的基础
1.1 期望、方差与标准差
用来刻画随机变量某一方面特征的常数被称为随机变量的数字特征,其常用的有:
数学期望:
在概率论和统计学中,数学期望(mean)是试验中每次可能结果的概率乘以其结果的总和,是最基本的数学特征之一。它反映随机变量平均取值的大小。
需要注意的是,期望值并不一定等同于常识中的“期望”——“期望值”也许与每一个结果都不相等。期望值是该变量输出值的平均数。期望值并不一定包含于变量的输出值集合里。大数定律表明,随着重复次数接近无穷大,数值的算术平均值几乎肯定地收敛于期望值。举个简单的例子:掷骰子游戏中,玩家摇到红色(1和4)可以赢得90元,摇到蓝色(2、3、5、6)输掉60元。而摇到红色的概率为1/3,蓝色的概率为2/3,也就是说玩家有1/3的期望获得90元,而商家有2/3的 期望获得60元,客观来说一次游戏玩家获得的金钱为30,而商家获得40元。
对于离散型(随机变量只取得有限个值或无穷能按次序一一列出)的随机变量的一切可能取值 x x xi与对应的概率 p p p( x x xi)乘积之和称为该离散型随机变量的数学期望(若该求和绝对收敛),记作 E ( x ) E(x) E(x)或者 μ \mu μ,他是简繁算数平均的一种推广, 类似加权平均,即 μ = ∑ k = 1 ∞ x k p k \mu=\sum_{k=1}^{\infty}{x_kp_k} μ=∑k=1∞xkpk。离散的才有均值。
对于连续型随机变量 x x x的概率密度函数为 f ( x ) f(x) f(x),若积分绝对收敛,则积分的值 ∫ − ∞ ∞ x f ( x ) d x \int_{-\infty}^{\infty}xf(x)dx ∫−∞∞xf(x)dx为随机变量的数学期望,即 μ = ∫ − ∞ ∞ x f ( x ) d x \mu=\int_{-\infty}^{\infty}xf(x)dx μ=∫−∞∞xf(x)dx。连续的有数学期望可是没有均值。
方差:
方差是在概率论和统计方差衡量随机变量或一组数据时离散程度的度量。概率论中方差用来度量随机变量和其数学期望(即均值)之间的偏离程度。统计中的方差(样本方差)是每个样本值与全体样本值的平均数之差的平方值的平均数。在许多实际问题中,研究方差即偏离程度有着重要意义。简单来说就是描述一个变量离其期望值的距离,即各个误差的平方累加,再除以总数,即对于离散型随机变量 σ 2 = ∑ ( X − μ ) 2 N \sigma^2=\frac{\sum(X-\mu)^2}{N} σ2=N∑(X−μ)2,其中 σ 2 \sigma^2 σ2为总体方差, X X X为变量, μ \mu μ为总体均值, N N N为总体例数。而对于连续型随机变量 σ 2 = ∫ ( x − μ ) 2 f ( x ) d x \sigma^2=\int{(x-\mu)^2f(x)dx} σ2=∫(x−μ)2f(x)dx。
标准差:
标准差是方差的算术平方根,用 σ \sigma σ表示,标准差也被称为标准偏差,反映了一个数据集的离散程度。如下图(概率密度函数 f ( x ) f(x) f(x))通过标准差可以直观得到距离平均值 μ \mu μ到 μ + σ \mu+\sigma μ+σ之间的概率。注意,概率密度函数是对连续随机变量定义的,且它本身并不是概率,只有对连续随机变量的概率密度函数在某区间内进行积分后才能得到概率,对于一个连续型随机变量而言,他取任何固定值的概率都为0,也就是说考察随机变量在某一点的概率取值是没有意义的。因此,在考察连续型随机变量的分布时,讨论的是它在某个区间的概率取值。这时就要借助其累积分布函数( F ( X ) F(X) F(X))。

补充:概率分布函数PDF和累积分布函数CDF
累积分布函数(Cumulative Distribution Function, CDF),简称分布函数,对于随机变量
X
X
X,如下定义的函数F
F
(
X
)
=
P
(
X
≤
x
)
−
∞
<
x
<
∞
F(X)=P{(X\leq x)} \quad\quad\quad\quad -\infty<x<\infty
F(X)=P(X≤x)−∞<x<∞
称为
X
X
X的累积分布函数,对于任意给定的实数
X
X
X,分布函数等于该随机变量小于等于
x
x
x的概率。
概率分布函数(Probability Density Function, PDF):对于连续型随机变量
X
X
X的累积分布函数
F
(
x
)
F(x)
F(x),如果存在一个定义在
x
x
x轴上的非负函数
f
(
x
)
f(x)
f(x),使得对于任意实数
x
x
x,有下式成立
F
(
X
)
=
∫
−
∞
x
f
(
t
)
d
t
F(X)=\int_{-\infty}^{x}f(t)dt
F(X)=∫−∞xf(t)dt
则称
f
(
x
)
f(x)
f(x)为
X
X
X的概率密度函数,显然,当概率密度函数存在的时候,累积分布函数是概率密度函数的积分,两者的图像如下所示:

1.2 一维高斯函数
高斯函数(Gaussian Function),也简称为Gaussian,是以数学家Carl Friedrich Gaussian的名字命名的。其一维形式如下:
f
(
x
)
=
a
e
−
(
x
−
b
)
2
2
c
2
(
a
>
0
)
\Large f(x) = ae^{-\frac{(x-b)^2}{2c^2}} \\ (a>0)
f(x)=ae−2c2(x−b)2(a>0)
高斯函数的一维图像是对称的钟形(bell curve),以上公式中各个字符在图像中的含义为:a是曲线尖峰的高度,b是尖峰中心的坐标,c称为标准方差,表征的是bell钟状的宽度。高斯函数广泛应用于模糊、正态分布统计、卷积等方面,具体来说可以做荧光笔效果、毛玻璃效果、边缘平滑、抗锯齿等。

由高斯积分公式
∫
−
∞
∞
e
−
x
2
d
x
=
π
\int_{-\infty}^{\infty}{e^{-x^2}}dx=\sqrt{\pi}
∫−∞∞e−x2dx=π,令
y
=
x
−
b
y=x-b
y=x−b,可得
d
x
=
d
y
dx=dy
dx=dy,令
z
2
=
y
2
2
c
2
z^2=\frac{y^2}{2c^2}
z2=2c2y2,可得
d
y
=
2
c
d
z
dy=\sqrt{2}cdz
dy=2cdz。
则
∫
−
∞
∞
a
e
−
(
x
−
b
)
2
2
c
2
d
x
\int_{-\infty}^{\infty}{ae^{\frac{-(x-b)^2}{2c^2}}}dx
∫−∞∞ae2c2−(x−b)2dx
当且仅当
a
=
1
c
2
π
a=\frac{1}{c\sqrt{2\pi}}
a=c2π1时上式积分值为1,在这种情况下,高斯是正态分布随机变量的概率密度函数。而正态分布就是使
b
=
μ
,
c
=
σ
b=\mu,c=\sigma
b=μ,c=σ,此时:
f
(
x
)
=
1
σ
2
π
e
−
(
x
−
μ
)
2
σ
2
f(x)=\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{(x-\mu)^2}{\sigma^2}}
f(x)=σ2π1e−σ2(x−μ)2
当
μ
=
0
,
σ
2
=
1
\mu=0,\sigma^2=1
μ=0,σ2=1时为标准正态分布,此时:
f
(
x
)
=
1
2
π
e
−
x
2
σ
2
f(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{\sigma^2}}
f(x)=2π1e−σ2x2
1.2二维高斯函数
二维高斯函数形式为:
f
(
x
,
y
)
=
A
e
−
(
(
x
−
x
0
)
2
2
σ
x
2
+
(
y
−
y
0
)
2
2
σ
y
2
)
\Large f(x,y)=Ae^{-(\frac{(x-x_0)^2}{2\sigma_x^2}+\frac{(y-y_0)^2}{2\sigma_y^2})}
f(x,y)=Ae−(2σx2(x−x0)2+2σy2(y−y0)2)
其中A是幅值,
x
0
x_0
x0,
y
0
y_0
y0是中心点坐标,
σ
x
2
和
σ
y
2
\sigma_x^2和\sigma_y^2
σx2和σy2是方差,图示如下图所示,
A
=
1
A=1
A=1,
x
0
=
y
0
=
0
x_0=y_0=0
x0=y0=0,
σ
x
2
=
σ
y
2
=
1
\sigma_x^2=\sigma_y^2=1
σx2=σy2=1

同样,类似于一维高斯函数,得到的高斯函数如下:
G
(
x
,
y
)
=
1
2
π
σ
2
e
−
x
2
+
y
2
2
σ
2
\Large G(x,y) = \frac{1}{2\pi\sigma^2}e^{-\frac{x^2+y^2}{2\sigma^2}}
G(x,y)=2πσ21e−2σ2x2+y2
二、高斯滤波原理
2.1高斯图像分析
使用matlab直观的分析高斯图像,在实际的matlab编程中,高斯函数用到的参数有:
· ksize 高斯函数的大小
· sigma 高斯函数的方差
· center 高斯函数尖峰中心点坐标
· **bias ** 高斯函数尖峰中心点的偏移量,用于控制阶段高斯函数
为了方便直观的观察高斯函数不同参属下的结果图像,使用代码实现参数的自动递增,并且生成gif图像,完整代码如下:
function mainfunc()
% 测试高斯函数,递增的方法实现高斯函数参数的改变对整个高斯函数的影响,
% 并自动保存为gif格式输出。
% created by zhao.buaa 2016.09.28
% 引用https://blog.csdn.net/qinglongzhan/article/details/82348153中的代码,修改了视角,输入mainfunc();即可运行
%% 保存gif动画
item = 10; % 迭代次数
dt = 1; % 步长大小
ksize =20; % 高斯大小
sigma = 2; % 方差大小
filename = ['ksize-' num2str(ksize) '-sigma-' num2str(sigma) '--' num2str(sigma+dt*item) '.gif']; %必须预先建立gif文件
% main loop
for i = 1:item
center = round(ksize/2); % 中心点
bias = ksize*10/10; % 偏移中心点量
ksigma = ksigma(ksize, sigma, center, bias); % 构建核函数
tname = ['ksize-' num2str(ksize) '-sigma-' num2str(sigma) '-center-' num2str(center)];
figure(i), mesh(ksigma), title(tname);
%设置固定的x-y-z坐标范围,便于观察,axis([xmin xmax ymin ymax zmin zmax])
axis([0 ksize 0 ksize 0 0.008]); view([30, 30]);% 改变可视角度
sigma = sigma + dt;
% 自动保存为gif图像
frame = getframe(i);
im = frame2im(frame);
[I,map] = rgb2ind(im,256);
if i==1
imwrite(I,map,filename,'gif','Loopcount',inf, 'DelayTime',0.4);
else
imwrite(I,map,filename,'gif','WriteMode','append','DelayTime',0.4);
end
end;
close all;
%% 截断高斯核函数,截断的程度取决于参数bias
function ksigma = ksigma(ksize, sigma, center,bias)
%ksize = 80; sigma = 15;
ksigma=fspecial('gaussian',ksize, sigma); % 构建高斯函数
[m, n] =size(ksigma);
for i = 1:m
for j = 1:n
if( (i<center-bias)||(i>center+bias)||(j<center-bias)||(j>center+bias) )
ksigma(i,j) = 0;
end;
end;
end;
以上主要用到了fspecial这个matlab函数,该函数的官方解释为:
H = fspecial(‘gaussian’,HSIZE,SIGMA) returns a rotationally symmetric Gaussian lowpass filter of size HSIZE with standard deviation SIGMA (positive). HSIZE can be a vector specifying the number of rows and columns in H or a scalar, in which case H is a square matrix.
即高斯低通滤波,有两个参数,HSIZE表示模板尺寸,sigma为滤波器的标准差,可以看到 σ \sigma σ越大,钟形越胖(同一维高斯函数),同时整个高斯函数的尖峰逐渐减小,整体也更加平滑,也就是对图像的平滑效果也越明显。

保持其他参数不变,对上述高斯函数进行截断,即将上述代码中的 b i a s = k s i z e ∗ 10 / 10 bias = ksize*10/10 bias=ksize∗10/10;改为 b i a s = k s i z e ∗ 3 / 10 bias = ksize*3/10 bias=ksize∗3/10,则结果如下图,也就是说对超过一定区域的原始图像信息不再考虑(可能类似于高斯模板有大有小),从而保证在更加合理的利用靠近高斯函数中心点的周围像素。

2.2高斯核与高斯函数的关系以及计算
以上关于高斯图像的讨论,并没有解释高斯模板的由来以及和高斯滤波的关系,其实高斯滤波用的就是高斯函数图像的特性进行的。简单来说就是高斯滤波器是一类根据高斯函数的形状来选择权值的线性平滑滤波器。在对图像进行卷积的时候其实是对图像进行点操作,用所求像素点周围的像素通过模板的权值计算得到新的像素值。而图像形状的不同也就代表了不同的参数,从而得到不同的模板。还是以上面程序中提到的fspecial函数为例,看看怎么计算高斯模板。
常用零均值离散高斯滤波器函数进行计算,上面提到二维高斯函数的形式为
G
(
x
,
y
)
=
1
2
π
σ
2
e
−
x
2
+
y
2
2
σ
2
G(x,y) = \frac{1}{2\pi\sigma^2}e^{-\frac{x^2+y^2}{2\sigma^2}}
G(x,y)=2πσ21e−2σ2x2+y2(曲线积分面积为1),而在图像上是离散的点,将该函数离散化得到:
H
(
i
,
j
)
=
1
2
π
σ
2
e
−
(
i
−
k
−
1
)
2
+
(
j
−
k
−
1
)
2
2
σ
2
\Large H(i,j) = \frac{1}{2\pi\sigma^2}e^{-\frac{(i-k-1)^2+(j-k-1)^2}{2\sigma^2}}
H(i,j)=2πσ21e−2σ2(i−k−1)2+(j−k−1)2
高斯卷积核H:(2k+1)×(2k+1),
σ
\sigma
σ为方差。
验证fspecial的计算:在matlab中输入 k = f s p e c i a l ( ′ g a u s s i a n ′ , 3 , 1 ) ; k=fspecial('gaussian',3, 1); k=fspecial(′gaussian′,3,1);,得到的kernel如下:

对于上述公式,取k=1,
σ
=
1
\sigma=1
σ=1,即可得到3×3的高斯卷积核如下:
KaTeX parse error: Undefined control sequence: \matrix at position 13: H = \left[ \̲m̲a̲t̲r̲i̲x̲{ \frac{1}{2\…
然而计算出的高斯卷积核还应该进一步归一化,也就是计算出来的高斯模板中各个数值其和必须为1,因为不归一化计算出来系的像素值会偏离原来的像素范围。归一化如下所示:
KaTeX parse error: Undefined control sequence: \matrix at position 13: H = \left[ \̲m̲a̲t̲r̲i̲x̲{ 0.0585 & 0.…
2.3 高斯核与高斯模板的关系
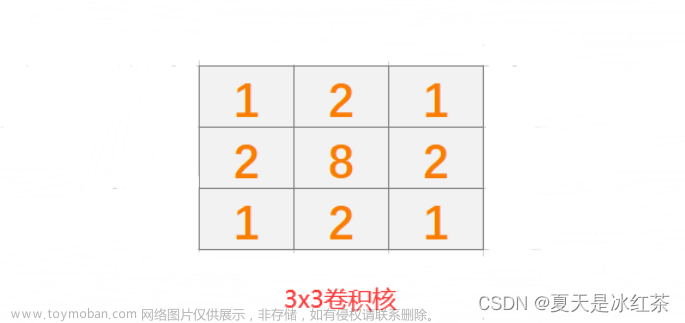
为了区别,暂且把以上计算出来的称为高斯核吧,而我们经常会用到一些形如以下的高斯模板,那么这个高斯模板和高斯核有什么关系呢,高斯模板实际上也就是模拟高斯函数的特征,具有对称性并且数值由中心向四周不断减小,这个模板刚好符合这样的特性,并且非常简单,容易被大家接受,于是就比较经典!
KaTeX parse error: Undefined control sequence: \matrix at position 21: …c{1}{16}\left[ \̲m̲a̲t̲r̲i̲x̲{ 1 & 2 & 1\\…
2.4 OpenCV中cvSmooth函数的用法
但是以上这样一个简单的矩阵是远远不能满足我们对图像处理的要求的,我们需要按照自己的要求得到更加精确的模板,那么接下来我们先看看OpenCV中高斯核的计算,紧接着再进一步编程实现自己想要的高斯模板。
OpenCV中GaussianBlur的原型为:
void cv::GaussianBlur ( InputArray src,
OutputArray dst,
Size ksize,
double sigmaX,
double sigmaY = 0,
int borderType = BORDER_DEFAULT
)
关于该函数的官方文档如下:
https://docs.opencv.org/4.x/d4/d86/group__imgproc__filter.html#gaabe8c836e97159a9193fb0b11ac52cf1
Blurs an image using a Gaussian filter.
The function convolves the source image with the specified Gaussian kernel. In-place filtering is supported.
Parameters
src input image; the image can have any number of channels, which are processed independently, but the depth should be CV_8U, CV_16U, CV_16S, CV_32F or CV_64F.
dst output image of the same size and type as src.
**ksize ** Gaussian kernel size. ksize.width and ksize.height can differ but they both must be positive and odd. Or, they can be zero’s and then they are computed from sigma.
sigmaX Gaussian kernel standard deviation in X direction.
sigmaY Gaussian kernel standard deviation in Y direction; if sigmaY is zero, it is set to be equal to sigmaX, if both sigmas are zeros, they are computed from ksize.width and ksize.height, respectively (see getGaussianKernel for details); to fully control the result regardless of possible future modifications of all this semantics, it is recommended to specify all of ksize, sigmaX, and sigmaY.
borderType pixel extrapolation method, see BorderTypes. BORDER_WRAP is not supported.
也就是说,高斯核的Size必须是正奇数或者也可以是0,当为0时,可以通过sigma进行计算,另外sigmaX和sigmaY分别代表X、Y方向的均方差。当sigmaY=0时,其值与sigmaY相同,而当两者皆没有给出时,可以通过Ksize进行计算。其中用到了getGaussianKernel()函数,而getGaussianKernel函数原型为:
Mat cv::getGaussianKernel ( int ksize,
double sigma,
int ktype = CV_64F
)
同样分析其官方文档:
Returns Gaussian filter coefficients.
The function computes and returns the (\texttt{ksize} \times 1) matrix of Gaussian filter coefficients:
[G_i= \alpha e^{-(i-( \texttt{ksize} -1)/2)^2/(2 \texttt{sigma}^2)},]
where (i=0…\texttt{ksize}-1) and (\alpha) is the scale factor chosen so that (\sum_i G_i=1).
Two of such generated kernels can be passed to sepFilter2D. Those functions automatically recognize smoothing kernels (a symmetrical kernel with sum of weights equal to 1) and handle them accordingly. You may also use the higher-level GaussianBlur.
-
Parameters
ksizeAperture size. It should be odd ( (\texttt{ksize} \mod 2 = 1) ) and positive.sigmaGaussian standard deviation. If it is non-positive, it is computed from ksize as
sigma = 0.3*((ksize-1)*0.5 - 1) + 0.8.ktypeType of filter coefficients. It can be CV_32F or CV_64F .
简单总结一下就是根据ksize去计算 σ \sigma σ的大小,根据公式 σ = 0.3 ( ( k s i z e − 1 ) × 0.5 − 1 ) + 0.8 \sigma=0.3((ksize-1)×0.5-1)+0.8 σ=0.3((ksize−1)×0.5−1)+0.8,反过来也可以根据 σ \sigma σ去计算核的大小。这里根据的是高斯分布的特点(如图所示,数值分布在(μ—3σ,μ+3σ)中的概率为0.9974),如果核矩阵更大,那么相应的Sigma也更大,相反,如果Sigma更大,那么核矩阵覆盖范围也更大。
2.5 编写计算高斯模板的自定义函数
编写了一个自定义的计算高斯模板的函数如下,在 σ \sigma σ缺省(等于0)时,通过OpenCV中的公式计算 σ \sigma σ值,同样,在高斯模板尺寸缺省时,通过该公式由 σ \sigma σ反过来计算模板大小,完整代码如下:
double ** createGuassion(int , double);
double ** createGuassion(int kSize, double sigma)
{
if (kSize%2==0 || kSize<0 || (kSize==0&&sigma==0))
{
return 0;//当模板大小为偶数、或者小于0、或者模板大小与sigma同时为0时返回
}
else if (kSize==0)
{
kSize = 2 * (sigma - 0.8) / 0.3 + 3;
kSize = round(kSize);//
if (kSize % 2 == 0)
{
kSize += 1;
}
}
else if (sigma == 0)
{
sigma = 0.3*((kSize - 1)*0.5 - 1) + 0.8;//sigma缺省时,利用该公式计算sigma
}
double **guass;//生成的高斯矩阵
double sum = 0;//用于归一化求和
double x2 = 0;
double y2 = 0;
int center = (kSize - 1) / 2;//高斯核中心点的行标和列标(从0开始计),所以必须保证kSize为奇数
guass = new double*[kSize];//注意,double*[k]表示一个有10个元素的指针数组
for (int i = 0; i < kSize; ++i)
{
//先创建一个kSize×kSize的模板矩阵
guass[i] = new double[kSize];
}
for (int i = 0; i < kSize; i++)
{
x2 = pow(double(i - center), 2); //高斯函数中的x平方
for (int j = 0; j < kSize; j++)
{
y2 = pow(double(j - center), 2);//高斯函数中的y平方
sum += guass[i][j] = exp(-(x2 + y2) / (2 * sigma*sigma));//赋值并累加
}
}
//归一化处理
if (sum != 0)
{
for (int i = 0; i < kSize; i++)
{
for (int j = 0; j < kSize; j++)
{
guass[i][j] /= sum;
}
}
}
return guass;
}
int main()
{
double **p = createGuassion(3, 1);
for (int i = 0; i < 3; ++i)
{
for (int j = 0; j < 3; ++j)
{
printf("%-9f\x20", *(*(p + i) + j));
//p+i表示a[i]的地址
//"%-9f中, '-'表示左对齐(无'-'默认为右对齐);9表示这个元素输出时占两个空格的空间
//"\x20"表示以十六进制数20所代表的字符,即空格(space的ASCII为32)
}
printf("\n");
}
printf("\n");
for (int i = 0; i < 3; ++i)
{
for (int j = 0; j < 3; ++j)
{
printf("%7.4f\x20", *(*(p + i) + j));
//p+i表示a[i]的地址
//"%-7.4f中, '-'表示左对齐(无'-'默认为右对齐);
//7.4表示这个元素输出时占7列,其中包括4个小数
}
printf("\n");
}
printf("\n");
return 0;
运行结果如下,上面是原输出,当取计算的4位小数时,结果与matlab中计算的一模一样,由此也验证了该函数的正确性。
0.075114 0.123841 0.075114
0.123841 0.204180 0.123841
0.075114 0.123841 0.075114
0.0751 0.1238 0.0751
0.1238 0.2042 0.1238
0.0751 0.1238 0.0751
另外分析在使用创建的高斯模板进行卷积的时候,二维函数处理应该是这样:
for(i=0;i<img.height;i++)
for(j=0;j<img.width;j++)
for(m=0;m<kSize;kSize++)
for(n=0;n<kSize;kSize++)
......
这样卷积算法的复杂度应该是O(height*width*kSize*kSize)
然而高斯函数具有可分离性,也就是说一个二维的高斯函数可以分解成相同的一维高斯函数,用其来处理两遍图像,效果一样,但是算法复杂度就变成了O(height*width*kSize*2),这样算法复杂度就会减小不少。
相应的模板函数变为:
//生成一维高斯模板,水平的和垂直方向上的模板是一样的,与上面的二维类似,只不过少计算一维
double* CreateMuban(int kSize ,double sigma)
{
double *gauss = new double[kSize];//声明一维模板
int radius = (kSize - 1) / 2;//这是高斯中心
double sum = 0;
for (int i = 0; i < kSize; i++)
{//高斯函数前面的常数项因为在归一化的时候将会消去,故这里不重复计算
gauss[i] = exp(-(i - radius)*(i - radius)/(2*sigma*sigma));
sum = sum + gauss[i];
}
for (int i = 0; i < kSize; i++)
{//归一化
gauss[i] = gauss[i] / sum;
}
return gauss;
}
//这里得到得guassian模板就是一维的,用来处理图像时,要分别进行两次操作,即对水平和垂直方向分别进行卷积。
2.6 边界点的处理
应该注意到在OpenCV中的GuassianBlur中有一个参数为BorderType,这就涉及到边界点的处理,因为卷积中如果一个像素点处于边界,周边没有足够的点,这个时候应该怎么处理?常见的方法要么是补0,要么就是把已有的点拷贝到另一点的对应位置,模拟出完整的矩阵。边界点的处理以及高斯的分布处理将放到卷积中总结。
参考文献:
百度百科
https://zhuanlan.zhihu.com/p/40060966
https://www.pianshen.com/article/1236562010/
https://blog.csdn.net/qinglongzhan/article/details/82348153文章来源地址https://www.toymoban.com/news/detail-413432.html
https://www.cnblogs.com/ping-36/articles/2810203.html
https://blog.csdn.net/qinglongzhan/article/details/82348153
https://docs.opencv.org/4.x/d4/d86/group__imgproc__filter.html#gaabe8c836e97159a9193fb0b11ac52cf1
https://www.cnblogs.com/bingdaocaihong/p/7007346.html文章来源:https://www.toymoban.com/news/detail-413432.html
https://blog.csdn.net/qinglongzhan/article/details/82348153
到了这里,关于高斯滤波及其原理的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!