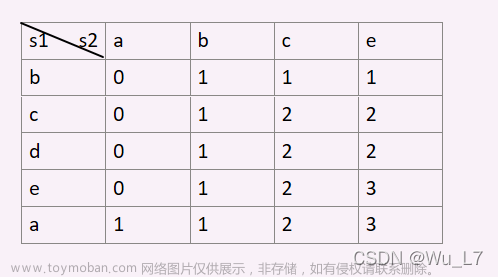
最长公共子序列
文章有些长,希望能够耐心看完,并且对你有帮助,文章是自己看了书之后,总结的,如果有什么错误的地方,欢迎指出。
一些基本的概念:
子序列: 原序列中删除若干个元素得到的序列,即原序列中可以不连续的一段
子串: 原序列中任意个连续的序列元素组成的序列,即原序列中必须连续的一段。
(两者的元素顺序必须和原序列中的顺序一样)
最长公共子序列: 一个序列即是X序列的子序列,也是Y序列的子序列,则该序列称为为X和Y的公共子序列。对于两个序列的公共子序列是不唯一的,因此,最长公共子序列顾名思义就是长度最长的公共子序列。
思路分析:
方一、从最优子结构去考虑
求最长公共子序列长度:
分析:
因为动态规划的题目是满足最优子结构(最优解包含其子问题的最优解)这一基本条件的,因此我们通过分析最优子结构的特征,从而推出最优值的递推式,然后从子问题最优解出发,求解出整个问题的最优解即可。
假设一个最优子结构情况,对于一个序列Z = {z1, z2, …… , zk}是 X = {x1, x2, ……, xm} 和 Y ={y1, y2 , ……, yn}的最长公共子序列,根据对最后一个元素考虑,我们可以分成三种情况来具体讨论:
1)xm = yn = zk
将xm和yn的值作为序列Z的最长公共子序列的最后一个元素,如果去掉xm和yn,那么对于序列Z的最长公共子序列的长度肯定会减小1,即c[i - 1] [j - 1] = c[i] [j] - 1; 因此,当xm = yn时的递推公式是: c[i] [j] = c[i - 1] [j - 1] + 1;
(为什么要将xm和yn值做为最长公共子序列最后一个元素?你想,两个序列相等的元素且都在最后一个,并且和已知最长公共子序列的最后一个元素相等,无论X和Y前面怎么取公共部分,是不是最后这两个元素都可以作为一个公共部分加入到公共子序列的末尾)
2)xm ≠ yn, xm ≠ zk
表明xm肯定不会作为最长公共子序列的最后一个元素,那么我们把xm去掉,对于{x1, x2,……, xm-1} 和 {y1, y2,……, yn -1}的最长公共子序列也还是{z1, z2,……, zk-1}
3)xm ≠ yn, yn ≠ zk
同理2)情况
由1)2)3)得最优值的递推式:
对于c[i] [j]数组:指只取X前i个元素和只取Y前j个元素能够得到的最长公共子序列的值(即存放最优子结构的值)。
由1)可知,如果xi = yj,那么可以从没有xi和yj的最优子结构即c[i - 1] [j - 1]转移过来
即 c[i] [j] = c[i - 1] [j - 1] + 1;
由2)3)可知,如果xi ≠ yj, 那么我们只需要取xi和yj-1最优子结构和xi-1和yj最优子结构的最大长度即可。
即c[i] [j] = max(c[i] [j - 1] , c[i - 1] [j] );
综上可以得出递推式:

自底向上求出问题的最优解:
对子结构考虑的最优情况,得出的递推式是对所有求子问题的最优解适用的,通过该递推公式,自底向上计算子问题的最优值,那么最后的答案也肯定是最优的(这也就是动态规划的最优子结构的特征)
代码:
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 1010;
char s1[N], s2[N];
int len1, len2;
int c[N][N];
int main()
{
//最优子结构状态值初始化(当然也可以不写,因为全局变量默认为0)
memset(c, 0, sizeof(c));
//输入序列s1和s2的长度
cin>>len1>>len2;
//输入需要求最长公共子序列的序列s1和s2
cin>>s1+1>>s2+1;
for(int i = 1; i <= len1; i ++){
for(int j = 1; j <= len2; j ++){
if(s1[i] == s2[j])c[i][j] = c[i - 1][j - 1] + 1;
else c[i][j] = max(c[i - 1][j], c[i][j - 1]);
}
}
cout<<c[len1][len2]<<'\n';
return 0;
}
求最长公共子序列内容:
分析:
对于一个最优子结构c[i] [j]的来源一共有三个,分别是
1)c[i] [j] = c[i - 1] [j - 1] + 1;
2)c[i] [j] = c[i - 1] [j] ;
3)c[i] [j] = c[i] [j - 1];
在自底向上计算最优值的时候,我们可以开一个临时的数组b[i] [j]去记录这3个来源,然后根据最值反向追踪最长公共子序列:
1)b[i] [j] = 1, 即表示取了x[i]或y[j]作为最长公共子序列的一部分,我们输出即可。
2)b[i] [j] = 2,即表示当前c[i] [j]的状态来自c[i - 1] [j],我们追踪c[i - 1] [j]
3)b[i] [j] = 3, 即表示当前c[i] [j]的状态来自c[i] [j - 1],我们追踪c[i] [j - 1]
代码:
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 1010;
char s1[N], s2[N];
int len1, len2;
int c[N][N];
int b[N][N];
void print(int i, int j){
if(i == 0 || j == 0)return;
if(b[i][j] == 1){
print(i - 1, j - 1);
cout<<s1[i];
}
else if(b[i][j] == 2)print(i - 1, j);
else print(i, j - 1);
}
int main()
{
//最优子结构状态值初始化
memset(c, 0, sizeof(c));
//输入序列s1和s2的长度
cin>>len1>>len2;
//输入需要求最长公共子序列的序列s1和s2
cin>>s1+1>>s2+1;
for(int i = 1; i <= len1; i ++){
for(int j = 1; j <= len2; j ++){
if(s1[i] == s2[j]){
c[i][j] = c[i - 1][j - 1] + 1;
b[i][j] = 1;
}
else if(c[i - 1][j] >= c[i][j - 1]){
c[i][j] = c[i - 1][j];
b[i][j] = 2;
}
else {
c[i][j] = c[i][j - 1];
b[i][j] = 3;
}
}
}
print(len1, len2);
// cout<<c[len1][len2]<<'\n';
return 0;
}
当然如果你不想浪费空间,你也可以不用这个临时数组b,直接通过c数组判断即可:
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 1010;
char s1[N], s2[N];
int len1, len2;
int c[N][N];
void print(int i, int j){
if(i == 0 || j == 0)return;
if(c[i][j] == c[i - 1][j - 1] + 1){
print(i - 1, j - 1);
cout<<s1[i];
}
else if(c[i][j] == c[i - 1][j])print(i - 1, j);
else print(i, j - 1);
}
int main()
{
//最优子结构状态值初始化
memset(c, 0, sizeof(c));
//输入序列s1和s2的长度
cin>>len1>>len2;
//输入需要求最长公共子序列的序列s1和s2
cin>>s1+1>>s2+1;
for(int i = 1; i <= len1; i ++){
for(int j = 1; j <= len2; j ++){
if(s1[i] == s2[j])c[i][j] = c[i - 1][j - 1] + 1;
else c[i][j] = max(c[i - 1][j], c[i][j - 1]);
}
}
print(len1, len2);
//cout<<c[len1][len2]<<'\n';
return 0;
}
方二、闫氏DP分析法(从集合的角度考虑):
分析:
很久之前在Acwing上学习后,写的题解(字丑):
我们通过f[i] [j]去表示所有A[1 ~ i]和B[1 ~ j]的公共子序列的集合,其表示的属性是最大值(即最长长度)。
我们通过最长公共子序列是否包含最后两个元素即a[i]和b[j]对这个集合来进行划分,可以分为4种情况:
- a[i]和b[j]相等
- a[i]和b[j]不相等,a[i]和bx匹配x在j之前
- a[i]和b[j]不相等,b[j]和ax匹配x在i之前
- a[i]和b[j]不相等,两数都没有匹配
对于f[i] [j] = f[i - 1] [j - 1] + 1覆盖情况1
对于f[i] [j] = max{f[i - 1] [j], f[i] [j - 1]}覆盖情况2 3 4文章来源:https://www.toymoban.com/news/detail-413587.html

 文章来源地址https://www.toymoban.com/news/detail-413587.html
文章来源地址https://www.toymoban.com/news/detail-413587.html
代码:
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1e3 + 5;
int n, m;
int f[N][N];
char a[N], b[N];
int main()
{
cin >> n;
cin >> a + 1;
cin >> m;
cin >> b + 1;
for(int i = 1; i <= n; i ++)f[i][0] = i;
for(int j = 1; j <= m; j ++)f[0][j] = j;
for(int i = 1; i <= n; i ++){
for(int j = 1; j <= m; j ++){
int diff;
if(a[i] == b[j])diff = 0;
else diff = 1;
f[i][j] = min({f[i - 1][j] + 1, f[i][j - 1] + 1, f[i - 1][j - 1] + diff});
}
}
// for(int i = 0; i <= n; i ++){
// for(int j = 0; j <= m; j ++){
// cout << f[i][j] << ' ';
// }
// cout << '\n';
// }
cout << f[n][m] << '\n';
return 0;
}
/*
状态表示:
集合:a前i 变成b前j需要的操作
属性:min
状态计算:
划分:根据最后一个元素从增、删、改进行划分
//替
1)A[i] == B[j] 不用进行操作
f[i][j] = f[i - 1][j - 1];
2)A[i] != B[j]
f[i][j] = f[i - 1][j - 1] + 1;
3)A[i] 增B[j](ai 和 bj - 1 对齐)
f[i][j] = f[i][j - 1] + 1;
4)A[i] 删 A[i](ai - 1 和 bj 对齐)
f[i][j] = f[i - 1][j] + 1;
状态转移:
*/
//状态表示:f[i][j]是以1~ai的序列和以1~bj的序列的最长的公共子序列长度
//当枚举到的两个元素相同时:
//说明可以将该元素加入到两个子序列的最长公共子序列上,因此就直接对于f[i][j]=f[i-1][j-1]+1,表示在1~a[i-1]和
//1~b[j-1]的公共最长子序列的基础上加1,将f[i-1][j-1]状态加一转移给f[i][j]
//因此我们转移公式就是:f[i][j]=f[i-1][j-1]+1
//当枚举到的两个元素不同:
//那我们肯定是不能够将他们加入到两个子序列的最长公共子序列上,因此我们要去寻找之前最长的公共子序列长度转移过来
//对于a[i]和b[j]不相等存在3中情况:
//1、a[i]属于a和b的最长公共子序列,a[i]和bx匹配x在j之前,那么我们就要从f[i][j-1]将状态转移过来,此时的状态就
//是到i,j为止最长的公共子序列长度
//2、b[j]属于a和b的最长公共子序列,b[j]和ax匹配x在i之前,那么我们就要从f[i-1][j]将状态转移过来此时的状态就是
//到i,j为止最长的公共子序列长度
//3、a[i]和b[j]都不属于a和b的最长公共子序列,我们应当是从f[i-1][j-1]去将状态转移过来,但对于f[i-1][j]和f[i][j-1]
//是已经将f[i-1][j-1]的状态包括在里面(因为这三者是相等的)
//因此我们转移公式就是:f[i][j]=max(f[i][j-1],f[i-1][j])
到了这里,关于最长公共子序列(详细代码 注释 分析 以及求出最长公共子序列内容方法)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!