四种方法解决01背包问题-Toy模板网

这篇具有很好参考价值的文章主要介绍了四种方法解决01背包问题。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

01背包问题

四种方法解决01背包问题

01背包问题可以用dp或者dfs的方法来做

dfs的好处在于：它可以找出所有的选择方案，如果题目需要找方案的个数或者输出所有方案，就只能够选择dfs，而如果是用来输出最值，那么还是dp好点

dp的好处在于：dp是用来找出最优的方案，dp在每个1~V的体积总能找出当前体积下的最优方案（贪心），那么到最后他显然是输出的最优的方案，而如果要找出方案的个数，dp就显得无能为力了

1.无优化版dp

四种方法解决01背包问题

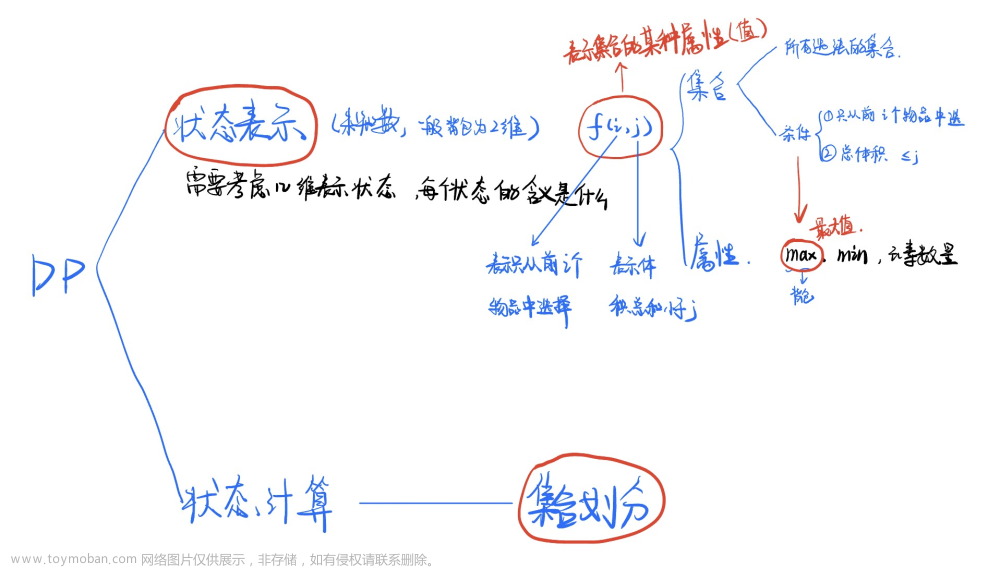
原问题：从前N个物品中选择，且体积不超过V的最大价值

子问题：从前i个物品中选择，且体积不超过j的最大价值

状态定义：dp[i][j]

集合：所有从前i个物品中选择，且提及不超过j的所有方案

属性：max

状态计算/集合划分：

根据最后一个不同点，可以分为不重不漏的两个子集

选择了第i个物品 dp[i-1][j-v[i]]+w[i]
没有选择第i个物品 dp[i-1][j]

由于dp数组表示当前集合的最大值，所以两个子集可以划分为dp[i-1][j-v[i]]+w[i],dp[i-1][j]

#include <iostream>
#include <algorithm>
using namespace std;
int N, V;
int v[1004],w[1004];
int res[1002][1002];
int maxn = -1;

int main()
{
	memset(res, 0, sizeof(res));
	cin >> N >> V;
	for (int i = 1;i <= N;i++)
		cin >> w[i] >> v[i];
	for(int i=1;i<=N;i++)
		for (int j = 1;j <= V;j++)
		{
			if (j < w[i])
			{
				res[i+1][j] = res[i][j];
			}
			else
			{
				res[i +1][j] = max(res[i][j], res[i][j - w[i]] + v[i]);
			}
		}
	//如果采用由当前元素是否选去计数下一个元素的挑选总价值的话(下标从1开始)
	//那么结果就要改为res[N+1][V],因为此时的集合为：dp[i+1][j]=从前i个元素挑选的总体积不超过j的集合
	//这个方法的好处是，下标可以从0开始，不用考虑边界问题（只要数组稍微略出一点）


	/*如果采用到当前元素才计数他的数组值应该是多少的话(下标从1开始)
	* 那么结果仍然是res[N][M]，因为此时的集合为:dp[i][j]=从前i-1个元素挑选的总体积不超过j的集合
	* 这个方法下标不可以从0开始，否则会访问到错误的地址值
	*/
	
	
	cout << res[N+1][V];
}

解释

在这里我记录一下dp的二维数组

i,j	1	2	3	4	5
1	2	2	2	2	2
2	2	4	6	6	6
3	2	4	6	6	8
4	2	4	6	6	8

四种方法解决01背包问题

表格外的红色箭头表示的是仅选择了第i个元素，而斜线表示在dp[i][j]的基础上再加上他的本身，从上到下的直线表示了不选本身，只是继承了dp[i-1][j]这个值

2.记忆化搜索

本题的dfs搜索树如下

四种方法解决01背包问题

#include <iostream>
#include <algorithm>
#include <cstring> 
using namespace std;
int N, V;
int v[1004], w[1004];
int dp[1004][1004];
/*普通搜索会tle，如果要用搜索的话，本题需要浪费一定的空间来进行记忆化搜索*/
int dfs(int i, int nowv)
{/*dfs判断当前第i个物品是否能够选择，nowv表示当前的容量*/
	if (i == N + 1)			//出界return
		return 0;
	if (dp[i][nowv] > 0)
		return dp[i][nowv];
	if (nowv < w[i])				//不能挑选
	{
		return dp[i][nowv] = dfs(i + 1, nowv);
	}
	else
	{
		return dp[i][nowv] = max(dfs(i + 1, nowv), dfs(i + 1, nowv - w[i]) + v[i]);
	}
}
int main()
{
	memset(dp, 0, sizeof(dp));
	cin >> N >> V;
	for (int i = 1;i <= N;i++)
		cin >> w[i] >> v[i];
	cout << dfs(1, V);
}

3.滚动数组法

时间复杂度没有降低，但是降低了空间复杂度

这里dp数组只用了两行来存储

#include <iostream>
#include <algorithm>
#include <cstring> 
using namespace std;
const int MAXN = 1100;
int v[MAXN], w[MAXN], dp[2][MAXN];
int main() {
    int N, V; cin >> N >> V;
    for (int i = 1; i <= N; ++i) cin >> w[i] >> v[i];
    /*我们知道dp的递推式是：dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i])
    从这个可以看出每一项的数组值都只会来自于dp数组的上面一行，而再上面的一行可以看到并不需要使用到
    所以我们就采用了一个滚动数组的方法，运用类似循环的方法来存储dp数组
    这里 在第二重for循环里 t2表示的是当前数组，t1表示的是上一个数组
    当整个dp循环结束后，t1表达的是结果(最下面的一行dp数组)
    这个方法并不需要去管他有多少个物品，可以降低空间复杂度
    */
    int* t1 = dp[0];            //滚动数组第一行指针
    int* t2 = dp[1];            //滚动数组第二行指针
    for (int i = 1;i <= N;i++)
    {
        for (int j = 1;j <= V;j++)
        {
            if (j < w[i])
                t2[j] = t1[j];
            else
                t2[j] = max(t1[j], t1[j - w[i]] + v[i]);
        }
        swap(t1, t2);
    }
    cout << t1[V] << endl;

}

4.一维优化dp法

这个方法比滚动数组法更加极致，仅用了一行来存储dp数组，极大降低了空间复杂度

dp的一维优化，首先要保证的是，在进行集合划分/状态计算时，前面两个子集合的值已经被递推出来了并且存在

如果我们仍采用j从0~V遍历的话，其实可以看到

四种方法解决01背包问题

枚举到j时，前面dp[i][0~j-1]这些状态已经被计算了，不是子集和dp[i-1][0~j-1]

所以我们应该用j从V~0遍历

这样子，当集合计算时，能够保证dp[i][j]的两个子集合的值存在

最后一个被计算的集合是dp[n][0]==dp[0]

dp[n][v]==dp[v]

文章来源地址https://www.toymoban.com/news/detail-413609.html

#include <iostream>
#include <algorithm>
#include <cstring> 
using namespace std;
const int MAXN = 1100;
int v[MAXN], w[MAXN], dp[MAXN];

int main()
{
	int N,V;
	cin >> N >> V;
	for (int i = 1;i <= N;i++)
		cin >> w[i] >> v[i];
	for(int i=1;i<=N;i++)
		for (int j = V;j >0;j--)
		{
			if (j < w[i])
				dp[j] = dp[j];
			else
			{
				dp[j] = max(dp[j], dp[j - w[i]] + v[i]);
			}
		}
	cout << dp[V];
	
}

到了这里，关于四种方法解决01背包问题的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！