安全多方计算之八：Mix-Match-Toy模板网

这篇具有很好参考价值的文章主要介绍了安全多方计算之八：Mix-Match。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

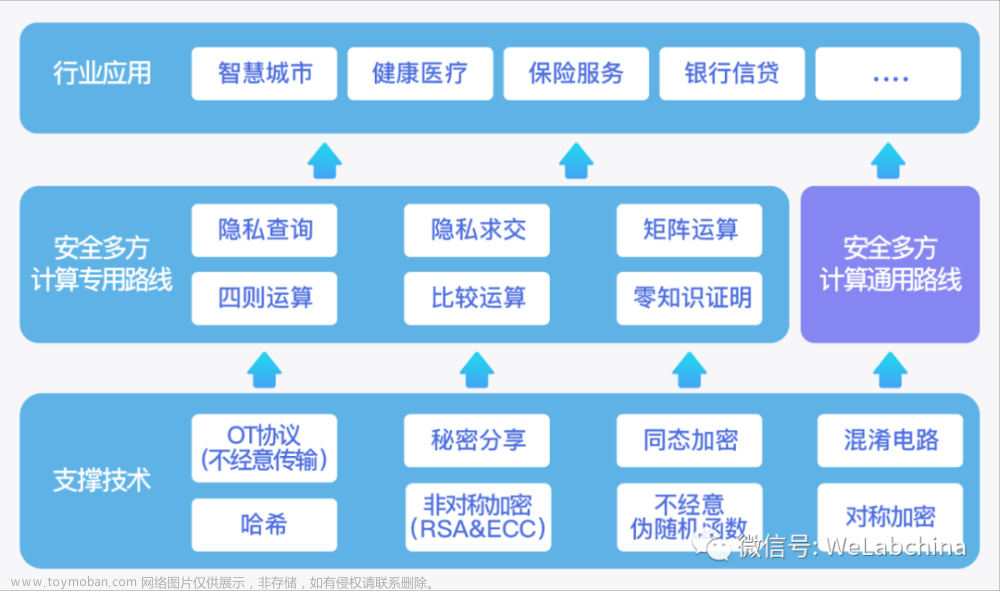
M.Jakobsson和A.Juels提出了基于Mix-Match的安全多方计算协议构造方法，该类协议包括Mix与Match两个阶段：

Mix阶段：通过构造混合网络，生成盲表（Blinded table）
Match阶段：通过执行PET协议进行查表，得到对应的输出

最后参与者共同解密输出，该类协议参与者之间所需传输的消息量较少，对于逻辑运算和Bit运算较为高效。

1. 混合网络

从直观上讲，混合网络是一个多方协议，协议的输入是一个密文表，该密文表中的密文与一组明文有着一一对应的关系。协议将这个密文表随机置换后得到另外一个密文表，输出的密文表和相同的一组明文也是一一对应的。即输出的密文表是输入密文表的随机置换。

混合网络的安全性在于攻击者无法确定输出密文表中的某一条密文与输入密文表中的哪一条密文是对应的。

基于ElGamal加密方案的混合网络

假定参与混合网络的 $n$ 个参与者都共享一个具备身份认证的广播信道（或存在一个公告板），将一个ElGamal加密方案的公钥 $y$ 公布给每个参与者。由参与者集合 $P$ 的某一个子集充当混合服务器（Mix Server）的角色，与 $y$ 对应的私钥使用 $(t, n)$ 门限方案在混合服务器中分享。

混合网络的参与者将自己的输入广播或传送到公告板上，混合网络的输入是一个ElGamal的密文序列 $(\alpha_1,\beta_1),(\alpha_{2},\beta_{2}),\cdots,(\alpha_{k},\beta_{k})$ 混合服务器依次独立地将混合网络输入的密文序列进行再次加密，随机置换顺序，混合网络的输出也是一个ElGamal密文序列 $(\alpha'_{\sigma(1)'},\beta'_{\sigma(1)}),(\alpha'_ {\sigma(2)'},\beta'_{\sigma(2)}), \cdots,(\alpha_{\sigma(k)'},\beta_{\sigma(k)})$ 其中 $(\alpha'_{i'}, \beta'_ {i})$ 表示 $(\alpha_{i},\beta_{i})$ 的随机再次加密结果, $\sigma$ 表示在 $k$ 个元素上的随机置换。

2. PET协议

假设 $(\alpha,\beta)$ 和 $(\alpha',\beta')$ 分别表示 $m_{1},m_{2}$ 使用ElGamal加密方案加密后的密文，参与相同明文测试协议的参与者在不解密的情况下通过执行协议判断 $(\alpha,\beta)$ 和 $(\alpha',\beta')$ 所对应的明文是否相同。

考虑密文 $(\varepsilon,\zeta) = (\alpha/\alpha',\beta/\beta')$ ，如果 $(\alpha, \beta)\equiv(\alpha',\beta')$ ，则 $\varepsilon, \zeta)$ 表示明文 $1$ 加密后的密文。

PET（Plaintext Equivalence Test） 协议的基本思路是让协议的参与者 $P_{i}$ 使用如下的方法隐藏 $(\varepsilon, \zeta)$ :

$P_{i}$ 选择 $z_{i} \in Z_{q}$ ,然后计算 $(\varepsilon_ {i}, \zeta_ {i}) = (\varepsilon^{z_{i}},\zeta^{z_{i}})$

如果 $(\alpha, \beta)\equiv(\alpha',\beta')$ ， $(\varepsilon, \zeta)$ 代表 $1$ 加密后的密文，则 $(\varepsilon_ {i}, \zeta_ {i})$ 仍是 $1$ 加密后的密文
如果 $(\alpha, \beta)\neq (\alpha',\beta')$ ， $(\varepsilon, \zeta)$ 代表 $m_{1}/m_{2}$ 加密后的密文，由于 $z_{i}$ 是一个随机数，所以 $(\varepsilon_ {i}, \zeta_ {i})$ 是一个随机数加密后的密文。

执行过程如下:

(1)每个协议参与者 $P_ {i}$ 选择 $z_ {i}$ 。 $P_{i}$ 对选择的 $z_{i}$ 公布一个Pedersen承诺， $C_{i}=g^{z_i}h^{r_i}$ ，其中 $r_{i} \in Z_{q}$ ， $h$ 是 $Z_{q}$ 的一个生产元， $log_{g}h$ 对所有的参与者都是未知的。
(2)每个 $P_ {i}$ 计算 $(\varepsilon_ {i}, \zeta_ {i}) = (\varepsilon^{z_{i}},\zeta^{z_{i}})$ ,然后广播 $(\varepsilon_ {i}, \zeta_ {i})$ 。
(3)每个 $P_ {i}$ 向其他参与者证明 $(\varepsilon_ {i}, \zeta_{i})$ 是与 $C_{i}$ 相关的并且是正确计算的。需要使用零知识证明协议证明他知道一个二元组 $z_ {i}, r_{i})$ ，使得 $C_{i}=g^{z_i}h^{r_i}$ ,并且 $\varepsilon_{i}=\varepsilon ^ {z_ {i}},\zeta_{i}=\zeta^{z_i}$ 。
(4)协议的参与者共同计算 $(\gamma,\delta)=(\prod^{i=1}_{n}\varepsilon_ {i}, \prod^{i=1}_{n}\zeta_{i}$ ，并解密 $(\gamma,\delta)$ 。
(5)如果解密结果是 $1$ ，则 $(\alpha, \beta)\equiv(\alpha',\beta')$ ；如果解密结果不为 $1$ ，则 $(\alpha, \beta)\neq (\alpha',\beta')$ 。

3. Mix-Match协议

使用 $B_{i}=\{b_{i1},b_{i2},\cdots,b_ {ik}\}$ 表示参与者 $P_{i}$ 的输入，基于Mix-Match的安全多方计算协议目标就是正确计算
$f(B_{1}, B_ {2},\cdots,B_{n})$ ，同时保证 $P_{i}$ 的输入 $B_{i}$ 的保密性。

执行步骤如下：

（1）构建门电路

计算之前，所有协议的参与者将需计算的函数 $f$ 用一个由若干门电路组成的单向图 $C_f$ 来表示。假设 $C_{f}$ 由 $N$ 个门电路组成，记作 $G_ {1},G_{2},\cdots, G_{N}$ 。不失一般性，假设每个门电路 $G_{i+1}$ 都比 $G_{i}$ 深，也就是说每个门电路的计算应该按照顺序从 $G_{1}$ 到 $G_{N}$ ， $G_{N}$ 的输出就是整个电路 $C_{f}$ 的输出。

（2）生成逻辑表

为描述简单起见，假定所有的门电路 $G_{i}$ 都只有两个输入值，一个输出值，并且输入值和输出值都可以用一个位来表示。

使用逻辑表 $T_{i}$ 表示 $C_{f}$ 中的门电路 $G_{i}$ ，由于假定 $G_{i}$ 都是二进制的门电路，则 $T_{i}$ 是一个4行3列的表。例如， $G_{i}$ 是一个AND门，则 $T_{i}$ 如下表所示。

左输入	右输入	输出
0	0	0
0	1	0
1	0	0
1	1	1

可以看出， $T_{i}$ 为一个标准的真值表，包含所有可能的输入与输出。 $T_{i}(u,v)$ 表示逻辑表 $T_{i}$ 的 $u$ 行 $v$ 列的值。

（3）输入阶段

所有协议参与者中使用秘密分享方案分享系统的私钥，系统的公钥是公开的。协议参与者 $P_i$ 将自己的输入 $B_i$ 使用公钥随机加密（如ElGamal加密方案），广播加密结果(或贴上公告牌)。

（4）混合阶段（Mix）

使用MN对 $T_{i}$ 进行混合，隐秘，随机置换。经过MN作用后，输出盲表 $\bar{T_{1}},\bar{T_{2}},\cdots,\bar{T_{N}}$ 。 $\bar{T_{i}}$ 表示经过MN混合网络加密、隐秘、随机置换后的逻辑盲表(只有随机行置换，列的顺序不变)。

（5）匹配阶段（Match）

每个协议参与者使用PET协议将加密的输入与混合后的逻辑表进行比较，即查表。和普通的查表不一样的地方在于，Match比较的是密文，所以要使用PET协议，查完一个盲表即是计算了一个门电路，每个参与者依次计算所有的门电路即可得到函数的输出，这个输出也是加密的。

对于组成 $C_{f}$ 的门电路 $G_{1},G_ {2},\cdots,G_ {N}$ ，协议的每个参与者 $P_{i}$ 独立的进行如下计算：假设 $l_{i}$ 和 $r_{i}$ 分别表示 $G_{i}$ 输入的密文， $P_{i}$ 使用PET协议对二元组 $l_{i},r_{i})$ 和 $\bar{T_{i}}$ 中的每一行的前两项进行比较。

如果 $PET(l_{i},\bar{T_{i}}[u,1])=1$ 且 $PET(r_{i},\bar{T_{i}}[u,2])=1$ ，则 $G_{i}$ 的输出应该是 $\bar{T_{i}}[u,3]$ 。 $P_{i}$ 分别对 $u=1,2,3,\cdots$ 进行比较,直到发现匹配的一行为止。

（6）输出阶段

计算完 $G_{N}$ 后， $P_{i}$ 得到了 $O_{N}$ ，即 $G_{N}$ 的输出，这个输出结果也是 $f$ 的输出结果。所有协议的参与者 $P_{i}$ 共同解密 $O_{N}$ ，即可得到正确的计算结果。

如果参与者 $P_{i}$ 提供了错误的输入，即该参与者所提供的输入密文不对应任何一个有效的位，则匹配一个 $\bar{T_{i}}$ 就会找不到匹配的行，由此可发现 $P_{i}$ 提供了错误的输入。其他参与者发现 $P_{i}$ 有欺诈行为后，可将 $P_{i}$ 驱逐出协议的执行，有正确性行协议的参与者一起重新执行协议。Mix-Match 协议的安全性在很大程度上依赖于混合网络的安全性。

Mix-Match协议可以比较容易地扩展到非二进制门电路的形式，如果 $G_{i}$ 有 $j$ 个输入，则 $G_{i}$ 对应的逻辑表的输人部分也有 $j$ 列，相应的， $T_{i}$ 应该有 $2^{j}$ 行。如果 $G_{i}$ 需要不止一个输出，则扩展 $G_{i}$ 对应的逻辑表 $T_{i}$ ，使 $T_{i}$ 的输出部分具有多个值即可。如果 $C_{f}$ 需要多个值的输出，则只需简单地将最后的若干门电路 $G_{N-k^{\prime}},G_{N-k+1'}, \ldots, G_{N}$ 的输出作为 $C_{f}$ 的输出，在输出阶段进行多次共同解密即可。

使用Mix-Match的协议所需要传输的信息量较少，广播传输的信息量是 $O (n N)$ ，其中 $n$ 是协议参与者的数量， $N$ 是需要计算的函数被表示为门电路之后电路中门的数量。

4. 百万富翁问题的Mix-Match解决方案

问题描述

Alice拥有财富为A，Bob拥有财富为B，其中 $A=a_1a_2,B=b_1b_2$ ，Alice与Bob需要在不泄露 $A, B$ 的前提下，计算 $F (A, B)$ 。 $\begin{cases} 0 \;\;\; if \; A=B \\ \\1 \;\;\; if \; A>B \\ \\2 \;\;\; if \; A<B \end{cases}$

（1）构建门电路

$F (A, B)$ 可以通过包含3个门 $G_1,G_2,G_3$ 的两层门电路来构造。其中 $G_1,G_2$ 构成第一层， $G_1$ 的输入为 $a_1,b_1$ ，输出为 $o_1$ ， $G_2$ 的输入为 $a_2,b_2$ ，输出为 $o_2$ ； $G_3$ 构成第二层，输入为 $o_1,o_2$ ，输出为 $F (A, B)$ 。

安全多方计算之八：Mix-Match
（2）生成逻辑表

为 $G_1,G_2,G_3$ 生成逻辑表 $T_1,T_2,T_3$ （包含所有输入及对应输出），其中 $o_1,o_2$ 的输出逻辑与 $F (A, B)$ 一致。 $o_i(i=1,2) = \begin{cases} 0 \;\;\; if \; a_i=b_i \\ \\1 \;\;\; if \; a_i>b_i \\ \\2 \;\;\; if \; a_i<b_i \end{cases}$ 针对逻辑表 $T_1,T_2,T_3$ ，需要对其进行编码，确保每组输入都是被唯一定义的。编码规则如下：