🌇个人主页:_麦麦_
📚今日名言:繁华落尽,我心中仍有花落的声音。一朵,一朵,在无人的山间轻轻飘落。——席慕蓉《桐花》

目录
一、前言
二、正文
1.归并排序
1.1 基本思想
1.2【递归版】具体实现
1.3【递归版】代码部分
1.4【非递归版】具体实现
1.5【非递归版】代码部分
1.6特性总结
2.计数排序
2.1基本思路
2.2具体实现
2.3代码部分
2.4特性总结
三、结语
一、前言
在本篇文章中,将会为小伙伴们详细的讲解“归并排序”。不过说到这里,有的小伙伴可能就会说了标题中不是还有“计数排序”嘛,这到底是什么呢?其实在前文中我们所展现的关于排序的思维导图是属于比较排序的,而除了比较排序之外,另一类排序就是非比较排序。而计数排序恰恰是非比较排序中一类相对常见的排序,所以也拿出来向小伙伴们介绍啦!
那么比较排序和非比较排序的区别在什么地方呢?顾名思义,比较排序需要对元素进行比较从而得出符合预期的排序,而非比较排序则无须对元素进行比较就能够得到预期的排序。至于如何实现归并排序和计数排序,那么就好好往下看叭!
二、正文
1.归并排序
1.1 基本思想
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有 序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
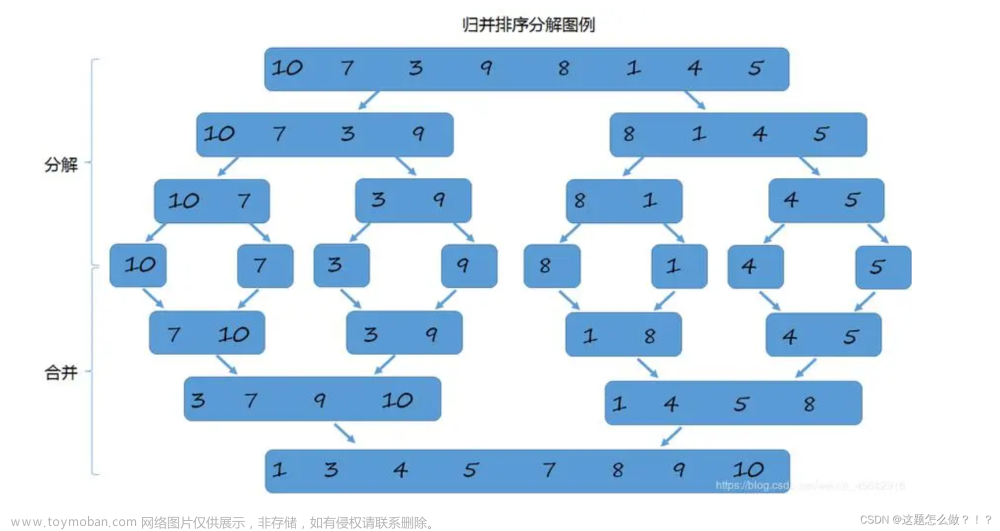
简单来说,就是相比于直接让一个无序的序列变得有序,合并两个有序的序列要更为简单一些,因此我们就可以逐渐细分,将一个无序的序列分为两个序列,使这两个序列有序后再进行合并。但是这两个序列要如何有序呢,再将这两个序列分为四个序列,使这四个序列有序后,再进行合并……直至分解后的序列无法进行再分解,这时的序列中就只有一个元素了,与其余序列比较以及后面的合并也最为简单,这也是递归版的归并排序的大致思路。
下面就分别用动态图和分解图来帮助小伙伴们更好的理解叭!


1.2【递归版】具体实现
那么这种思路体现在代码中,该如何实现呢。接下来我们就来讲讲递归版归并排序的代码思路。
在代码的书写中,大致分为两个模块,第一步是”归”,将大序列不断细分成两个小序列,第二个则是“并”,将小序列排好序后再将其合并。
那么具体该如何做呢?
在“归”这一步中,我们可以将这个序列不断对半分开,可以不是严谨的对半,由于我们本文是对数组进行归并排序,因此只需要将数组首元素和末尾元素的下标相加除以2即可作为分隔序列的边界。那么不断切分到什么时候为止呢?相信小伙伴们很容易答出当这个序列只有一个元素的时候就无须再切分了,因为此时它已经是“有序”了。
在“并”这一步中,大致有两步。首先是让两个序列有序,然后就是将两个有序序列合并。我们先来讲讲合并这一步,在两个序列已经有序的前提下,我们只需对两个序列从头一一比较即可,以升序为例,当序列一的首元素较小时,我们就将该元素取出,反之则取出序列而的元素,接下来重复以上操作即可,最后当两个序列的元素全部取出后,我们就会发现这个由两个序列的元素组成的新序列也是有序的。不过这都是建立要合并的两个序列是有序的前提下,那么要如何做到呢。其实是很简单的,由于我们将序列不断切分至只有一个元素,那么此时的序列就是有序的,而这些最小单位的序列合并后由上面可以知道定然也是有序了呀,这也就是归并排序的奥妙所在。
下面我们就以升序的代码为例:
1.3【递归版】代码部分
//归并排序[递归]
void _MergeSort(int* arr, int begin, int end, int* tmp)
{
//区间只有一个元素
if (begin == end)
return;
int mid = (begin + end)/2;
//左区间归并
_MergeSort(arr, begin,mid, tmp);
//右区间归并
_MergeSort(arr, mid+1, end, tmp);
//排序
int begin1=begin;
int end1 = mid;
int begin2 = mid+1;
int end2 = end;
int i = begin;
while (begin1 <= end1 && begin2 <= end2)
{
if (arr[begin1] < arr[begin2])
tmp[i++] = arr[begin1++];
else
tmp[i++] = arr[begin2++];
}
while(begin1 <= end1)
tmp[i++] = arr[begin1++];
while (begin2 <= end2)
tmp[i++] = arr[begin2++];
//拷贝
memcpy(&arr[begin], &tmp[begin], sizeof(int) * (end-begin+1));
}
void MergeSort(int* arr, int n)
{
//申请一个数组用于归并排序
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc failed");
}
//排序
_MergeSort(arr, 0, n-1, tmp);
//释放
free(tmp);
tmp = NULL;
}
1.4【非递归版】具体实现
不过对于一名合格的程序猿来说,自然还要掌握排序的非递归版,因为当递归的深度太深的时候,程序就有可能无法正常运行,因此也就有了非递归版的归并排序。
在理解完递归版的归并排序之后,再来看看非递归其实就很简单了。我们会发现归并排序无非就是就是将大序列切分成一个个小序列再将小序列排好序后合并即可,因此我们是否可以采用循环的方式来实现呢,答案当然是肯定的啦。
不过在具体的代码实现上,小伙伴们的写法在一个地方可能会有所不同,就是拷贝数组的数组的时候,是将所有的相同长度的序列排好序后并合并后的拷贝到原数组上,用方言来说就是“梭哈”,还是当一对相同长度的序列排好序且合并后就马上拷贝到原数组。其实本质上两者并无本质区别,只是在对数组的边界判断会有所不同而已。
具体代码如下:
1.5【非递归版】代码部分
//归并排序[非递归梭哈版]
void MergeSortNonR1(int* arr, int n)
{
//申请一个数组用于归并排序
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc failed");
}
//排序
int gap = 1;
//所有相同长度的序列的归并
while (gap < n)
{
int i = 0;
int j = 0;
//一对序列的归并
for (i = 0; i < n; i += 2 * gap)
{
//划分边界
int begin1 = i;
int end1 = i + gap - 1;
int begin2 = i + gap;
int end2 = i + 2 * gap - 1;
//边界判断
if (end1 > n - 1 || begin2 > n - 1)
{
break;
}
if (end2 > n - 1)
{
end2 = n - 1;
}
while (begin1 <= end1 && begin2 <= end2)
{
if (arr[begin1] < arr[begin2])
tmp[j++] = arr[begin1++];
else
tmp[j++] = arr[begin2++];
}
while (begin1 <= end1)
tmp[j++] = arr[begin1++];
while (begin2 <= end2)
tmp[j++] = arr[begin2++];
memcpy(&arr[i], &tmp[i], sizeof(int) * gap);
//增大序列长度
gap *= 2;
}
}
}
//归并排序[非递归非梭哈版]
void MergeSortNonR2(int* arr, int n)
{
//申请一个数组用于归并排序
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc failed");
}
//排序
int gap = 1;
//所有相同长度的序列的归并
while (gap < n)
{
int i = 0;
int j = 0;
//一对序列的归并
for (i = 0; i < n; i += 2 * gap)
{
//划分边界
int begin1 = i;
int end1 = i + gap - 1;
int begin2 = i + gap;
int end2 = i + 2 * gap - 1;
//边界判断
if (end1 > n - 1)
{
end1 = n - 1;
begin2 = n;
end2 = n - 1;
}
if (begin2 > n - 1)
{
begin2 = n;
end2 = n - 1;
}
if (end2 > n - 1)
{
end2 = n - 1;
}
while (begin1 <= end1 && begin2 <= end2)
{
if (arr[begin1] < arr[begin2])
tmp[j++] = arr[begin1++];
else
tmp[j++] = arr[begin2++];
}
while (begin1 <= end1)
tmp[j++] = arr[begin1++];
while (begin2 <= end2)
tmp[j++] = arr[begin2++];
}
memcpy(arr, tmp, sizeof(int) * n);
//增大序列长度
gap *= 2;
}
}1.6特性总结
①归并的缺点在于需要O(N)的空间复杂度,归并排序的思考更多的是解决在磁盘中的外排序问题。
② 时间复杂度:O(N*logN)
③ 空间复杂度:O(N)
④ 稳定性:稳定
2.计数排序
2.1基本思路
计数排序的基本思想是对于给定的输入序列中的每一个元素x,确定该序列中值小于x的元素的个数(此处并非比较各元素的大小,而是通过对元素值的计数和计数值的累加来确定)。一旦有了这个信息,就可以将x直接存放到最终的输出序列的正确位置上。
例如,如果输入序列中只有17个元素的值小于x的值,则x可以直接存放在输出序列的第18个位置上。当然,如果有多个元素具有相同的值时,我们不能将这些元素放在输出序列的同一个位置上,因此,上述方案还要作适当的修改
通俗来说,就是通过计算序列中每个元素所出现的个数,就能过将这些元素按照我们的需求处于正确的位置,听起来是不会很神奇呀,那就接着往下看叭!
2.2具体实现
在了解完计数排序的基本思路后,那么到底该如何实现呢,那么就不卖关子啦。
首先我们需要额外创立一个数组来记录序列中每个元素所出现次数。那么创立之后,随之而来的就是这个数组要开多大呢?这就涉及到两种计数方式了,分别是绝对位置映射计数,而另一种就是相对位置映射计数。
对于绝对位置映射计数来说,序列的元素所出现的次数就存储在新数组以记录元素为下标的位置,比如说数字“3”出现了4次,那么我们就在新数组的下标为3的位置修改为4,表明数字“3”在序列中出现了4次。不过这种方式还是存在很大的弊端的,就是当这一串序列的数字并不连续集中的时候,数组就会有很多的元素为0,既浪费时间也浪费空间,因此就衍生出了相对位置映射计数。也就是我们代码实现所采用的方式。
对于相对位置映射计数,我们需要遍历序列,找到序列中的最大值和最小值,依据两者的差值来确定的数组的大小,而序列中的元素减去最小值后便可作为新数组的下标来存储出现的次数,是谓相对位置。
具体代码如下:
2.3代码部分
//计数排序
void CountSort(int* arr, int n)
{
//找出数组中最大数和最小数
int i = 0;
int max = arr[0];
int min = arr[0];
for (i = 0; i < n; i++)
{
if (arr[i] > max)
max = arr[i];
if (arr[i] < min)
min = arr[i];
}
int sz = max - min + 1;
//申请一个数组
int* a = (int*)malloc(sizeof(int) * sz);
if (a == NULL)
{
perror("malloc failed");
}
memset(a, 0, sizeof(int) * sz);
//记录元素出现的次数
for (i = 0; i < n; i++)
{
a[arr[i] - min]++;
}
//对数组进行排序
int num = 0;
for(i=0;i<sz;i++)
{
while (a[i]--)
{
arr[num++] =i+min;
}
}
}
2.4特性总结
① 计数排序在数据范围集中时,效率很高,但是适用范围及场景有限。
② 时间复杂度:O(MAX(N,范围))
③空间复杂度:O(范围)
④ 稳定性:稳定
三、结语
到此为止,关于归并排序和计数排序的讲解就告一段落了,而其他的排序也会在下面的文章中继续讲解,敬请期待呀!
关注我 _麦麦_分享更多干货:_麦麦_的博客_CSDN博客-领域博主
大家的「关注❤️ + 点赞👍 + 收藏⭐」就是我创作的最大动力!谢谢大家的支持,我们下期见! 文章来源:https://www.toymoban.com/news/detail-414450.html
文章来源地址https://www.toymoban.com/news/detail-414450.html
到了这里,关于【数据结构】——归并排序和计数排序的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!