安全多方计算之九：不经意传输-Toy模板网

这篇具有很好参考价值的文章主要介绍了安全多方计算之九：不经意传输。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

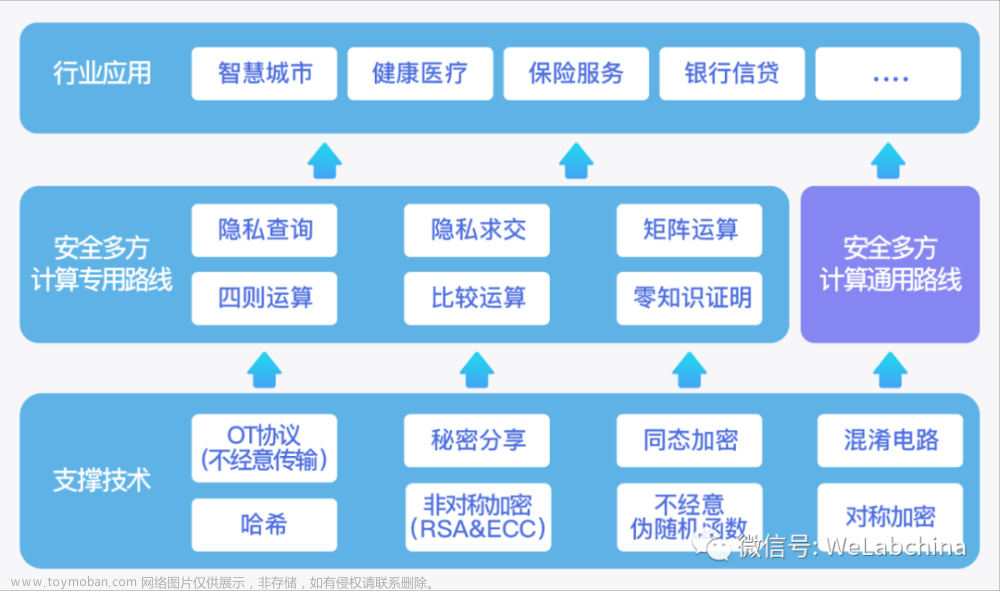
考虑这样的场景：A意欲出售许多个问题的答案，B打算购买其中一个问题的答案，但又不想让A知道他买的哪个问题的答案。即B不愿意泄露给A他究竟掌握哪个问题的秘密，此类场景可通过不经意传输协议实现。

不经意传输(OT，Oblivious Transfer)又称健忘传输或茫然传输，由Rabin于1981年提出。不经意传输是从一个消息集合秘密获取取部分消息的方法，该协议执行完毕后，接收方知道他是否收到这个秘密，但发送方却不知道。不经意传送是密码学中的基本构件，广泛应用于比特承诺、零知识证明、安全多方计算和电子支付等协议中。

不经意传输包括：1-out-of-2不经意传输、1-out-of-n不经意传输、m-out-of-n不经意传输。

1. Blum不经意传输

Blum不经意传输又称Rabin不经意传输，该协议中发送方以50%的概率传送一个秘密(整数 $n$ 的因数分解)给接收者，接收者有50%的机会收到这个秘密，有50%的机会什么也没有收到。

（1）A选择形式为 $4 r + 3$ 的两个个大素数，发送Blum数 $n=p\times q$ 给B，但将 $p, q$ 作为秘密保留。
（2）B随机选取一个整数 $x$ ，满足 $0<x<n,\operatorname{gcd}(x, n)=1$ ，即 $x$ 是比 $n$ 小且与 $n$ 互素的正整数，然后发送 $\equiv x^{2}(\bmod n)$ 给A。
（3）A根据已知的 $p, q$ 求出 $x^{2} \equiv a(\bmod p)$ 对应的 $2$ 个根，然后A随机选择其中的一个根发送给B。
（4）如果B接收到的是 $y$ 或 $n - y$ ，则B通过已知的 $x$ 和接收到的 $y$ 就可以得出 $p$ 和 $q$ ： $\operatorname{gcd}(x+y, n)=p$ 或 $\operatorname{gcd}(x+y, n)=q$ 。若 B 接收到的是 $x$ 或 $n - x$ ，则B得不出 $n$ 的任何信息。

2. 1-out-of-2不经意传输

$OT_{1}^{2}$ 不经意传输：Alice拥有两个消息 $M_1,M_2$ ，Bob得到其中的一份消息且Alice不知道是哪一个。

方法一

(1) Alice产生两个公开密钥/私人密钥对，共4个密钥，她把两个公开密钥发进给Bob。
(2) Bob生成一个对称算法(例如DES)密钥 $K$ ，选择Alice的一个公开密钥加密他的DES密钥 $K$ ，发送给 Alice（但不告诉她使用的是哪个公开密钥）。
(3) Alice每次使用一个她的私人密钥来解密Bob的密钥。Alice要么使用了正确的密钥并成功地解密Bob的DES密钥 $K$ ，要么使用了错误的密钥只是产生了一堆毫无意义而看上去又像一个随机DES密钥的位 $K ‘$ 。由于她不知道正确明文，所以不知道哪个是正确的。
(4) Alice分别使用产生的两个DES密钥加密她的两个消息，假设使用 $K$ 加密 $M_1$ ，使用 $K ‘$ 加密 $M_2$ ，将 $E_{K}(M_1),E_{K'}(M_2)$ 发送给 Bob。
(5) Bob收到一个用正确DES密钥加密的消息 $E_{K}(M_1)$ 和一个用无意义DES密钥加密的消息 $E_{K'}(M_2)$ ，当Bob用他的DES密钥解密每一份消息时，他能读其中之一，另一份在他看起来毫无意义。

此时Bob现在有了Alice两份消息中的一个（本例中是 $M_1$ ），而Alice不知道他能读懂哪一个。

方法二

（1)Alice选择两个随机数 $r_{0}, r_{1}$ ，发送给Bob。
（2)Bob选择一个随机数 $r$ ，用Alice的公钥 $d$ 加密 $r$ : $E_d(r)=r^{d}$ ，并且选择一个随机数（假设选择 $r_{0}$ ），计算 $S=r_0+E_d(r)$ ，发送给Alice。
（3)Alice计算 $S_{0}=S-r_{0},S_{1}=S-r_{1}$ ，并用私钥 $e$ 解密计算 $D_e(S_{0}),D_e(S_{1})$ ，然后发送 $M_{0}'=M_{0} \oplus D_e(S_{0}),M_{1}'=M_{1} \oplus D_e(S_{1})$ 给Bob。
（4）Bob计算 $M_{0}'\oplus r,M_{1}'\oplus r$ ，其中 $\begin{aligned} M_{0}' \oplus r &= M_{0} \oplus D_e(S_{0}) \oplus r \\ &= M_{0} \oplus D_e(S-r_0)\oplus r \\ &= M_{0} \oplus D_e(r_0+E_d(r)-r_0)\oplus r \\ &= M_{0} \oplus D_e(E_d(r)) \oplus r \\ &= M_{0} \oplus r \oplus r \\ &= M_{0}\end{aligned}$ Bob恢复了消息 $M_0$ ，同时Alice不知道Bob恢复的哪个消息。

3. 1-out-of-n不经意传输

$OT_{1}^{n}$ 不经意传输：Alice拥有 $n$ 个消息 $(M_{1}, M_{2}, \ldots, M_{n})$ ，Bob得到其中某一个 $M_{i}$ 且Alice不知道是哪一个。

系统参数：设 $p, q$ 均为素数， $p = 2 q + 1$ ， $G_{q}$ 是 $Z_{P}^{*}$ 的一个 $q$ 阶子群， $g, h$ 为 $G_{q}$ 的两个生成元， $Z_{q}$ 表示模 $q$ 的最小剩余集，协议两个参与方Alice和Bob都知道 $\left(g, h, G_{q}\right)$ 。

（1) Bob选择 $\in_{R} Z_{q}$ 和 $\leq i \leq n)$ ，计算 $y=g^{r} h^{i} \bmod p$ 发送给Alice;
（2) Alice对所有 $\leq j \leq n, k_{j} \in z_{q}$ ，计算 $a_{j}=g^{k_{j}} \bmod p, b_{j}=M_{j}\left(y / h^{i}\right)^{k_{j}} \bmod p$ 将 $\left(a_{1}, b_{1}\right),\left(a_{2}, b_{2}\right), \ldots,\left(a_{n}, b_{n}\right)$ 发送给Bob;
（3) Bob 计算 $\begin{aligned} b_{i} /a_{i}^{r} \bmod p &= M_{i}\left(y/h^{i}\right)^{k_{i}}/a_{i}^{r} \bmod p \\ &= M_{i}\left(g^{r} h^{i}/h^{i}\right)^{k_{i}}/{(g^{k_{j}})}^{r} \bmod p \\ &= M_{i} \end{aligned}$ Bob恢复了消息 $M_i$ ，同时Alice不知道Bob恢复的哪个消息。