【数据结构】稀疏矩阵的压缩存储（三元组表、十字链表）（C语言）-Toy模板网

这篇具有很好参考价值的文章主要介绍了【数据结构】稀疏矩阵的压缩存储（三元组表、十字链表）（C语言）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

稀疏矩阵是指矩阵中大多数元素为零的矩阵。从直观上讲，当非零元素个数低于总元素的30%时，这样的矩阵为稀疏矩阵。

1. 三元组表

1.1 三元组表的存储结构

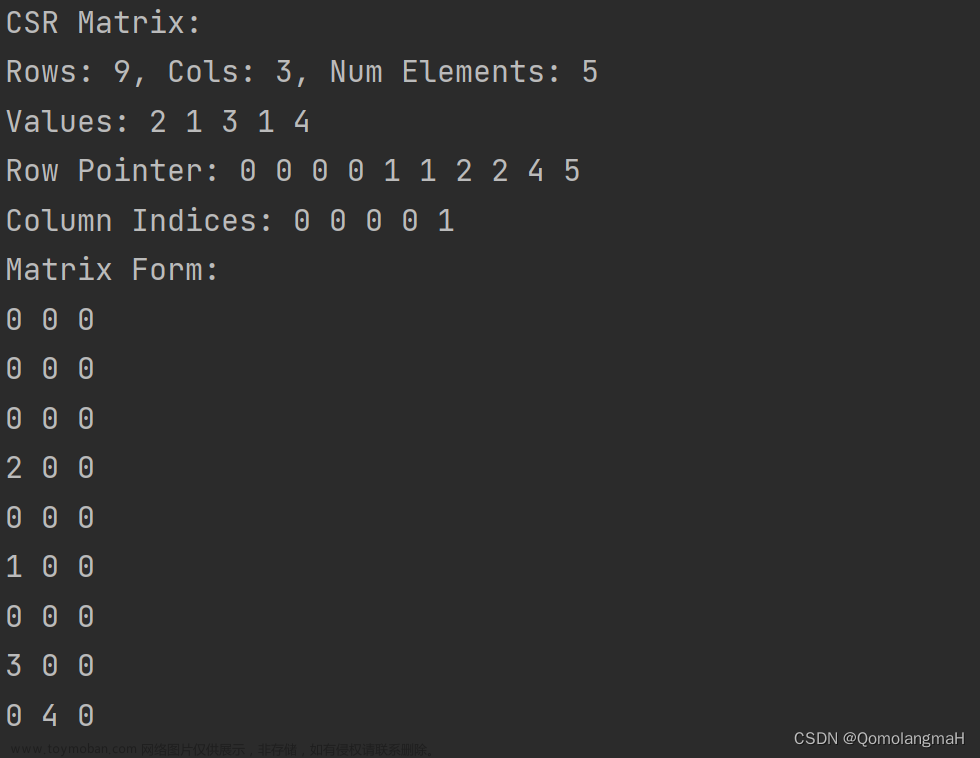
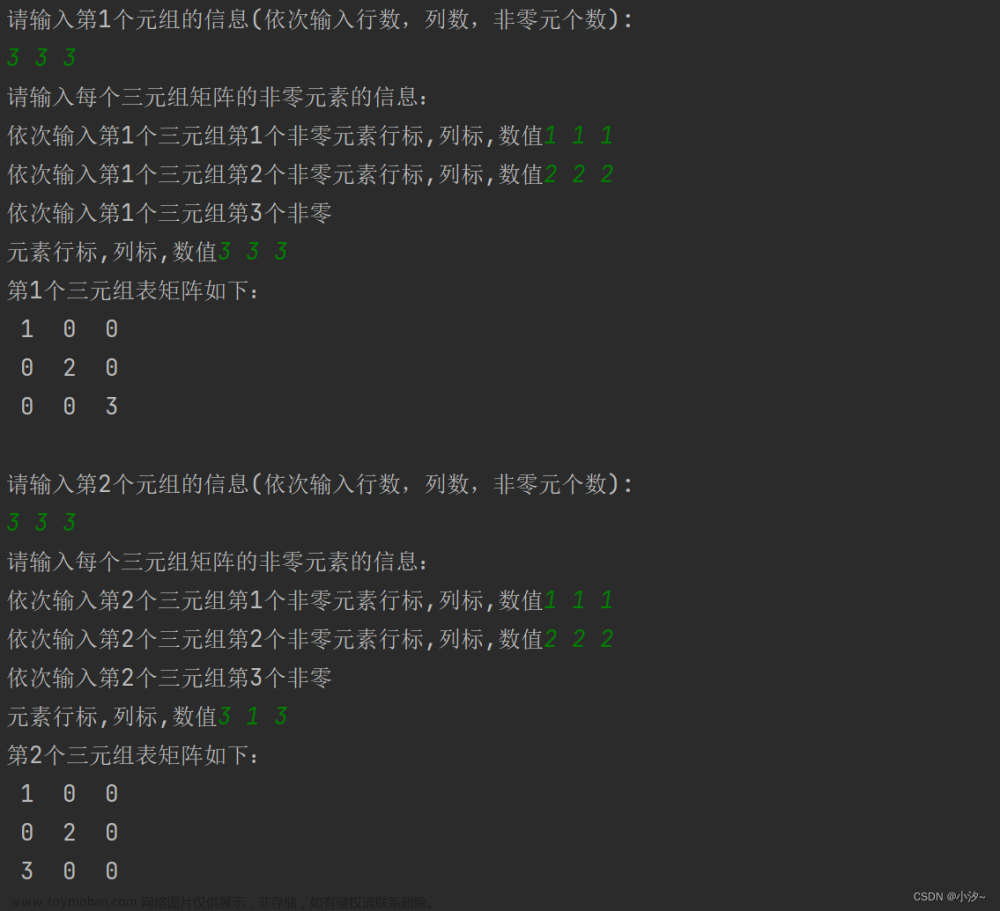
稀疏矩阵的三元组表表示法是指只存储非零元素，同时存储该非零元素在矩阵中所处的行号和列号的位置信息。
【数据结构】稀疏矩阵的压缩存储（三元组表、十字链表）（C语言）为方便处理，将稀疏矩阵中非零元素对应的三元组按“行序为主序”的一维结构体数组进行存放，将矩阵的每一行（行由小到大）的全部非零元素的三元组按列号递增存放，得到矩阵的三元组表。
【数据结构】稀疏矩阵的压缩存储（三元组表、十字链表）（C语言）
代码

# define MAXSIZE 1000				//设非零元素的个数最多为1000
/*三元组的存储结构*/
typedef struct {
	int row, col;					//该非零元素的行下标和列下标
	int e;							//该非零元素的值
}Triple;
/*三元组表的存储结构*/
typedef struct {
	Triple data[MAXSIZE + 1];		//非零元素的三元组表，下标从1开始
	int m, n, len;					//矩阵的行数、列数和非零元素的个数
}TSMatrix;

1.2 基于三元组表的矩阵转置

① 三元组表中的三元组行列互换。
② 三元组表重新按照行下标递增排序。

1.2.1 列序递增转置法
采用按照被转置矩阵三元组表A的列序递增的顺序进行转置，并依次送入转置后矩阵的三元组表B中。
【数据结构】稀疏矩阵的压缩存储（三元组表、十字链表）（C语言）

/*转置：列序递增转置法*/
void TransposeTSMatrix(TSMatrix* A, TSMatrix* B) {
	int i, j, k;
	B->m = A->n;
	B->n = A->m;
	B->len = A->len;
	if (B->len > 0) {
		j = 1;											//记录转置后的三元组在三元组表B中的下标值
		for (k = 1; k <= A->n; k++) {
			for (i = 1; i < A->len; i++) {				//从头至尾扫描三元组表A，寻找col值为k的三元组进行转置
				if (A->data[i].col == k) {
					B->data[j].row = A->data[i].col;
					B->data[j].col = A->data[i].row;
					B->data[j].e = A->data[i].e;
					j++;
				}
			}
		}
	}
}

1.2.2 一次快速转置法
只对三元组表A扫描一次，就使A中所有非零元的三元组“一次定位”直接放到三元组B中的正确位置上。

num[col]：用来存放三元组表A第col列中非零元素总个数
position[col]：用来存放转置前三元组表A中第col列中第一个非零元素在三元组表B中的存储位置（下标值）
position[1] = 1
position[col] = position[col - 1] + num[col - 1]（col > 1）
【数据结构】稀疏矩阵的压缩存储（三元组表、十字链表）（C语言）

/*一次定位快速转置法*/
void FastTransposeTSMatrix(TSMatrix* A, TSMatrix* B) {
	int col, t, p, q;
	int num[MAXSIZE], position[MAXSIZE];
	B->m = A->n;
	B->n = A->m;
	B->len = A->len;
	if (B->len) {
		for (col = 1; col <= A->n; col++)				//初始化num数组
			num[col] = 0;
		for (t = 1; t <= A->len; t++)
			num[A->data[t].col]++;						//扫描三元组表A，求num数组
		position[1] = 1;
		for (col = 2; col < A->n; col++)				//根据num数组求position数组
			position[col] = position[col - 1] + num[col - 1];

		for (p = 1; p <= A->len; p++) {					//扫描三元组表A，实现转置
			col = A->data[p].col;
			q = position[col];
			B->data[q].row = A->data[p].col;
			B->data[q].col = A->data[p].row;
			B->data[q].e = A->data[p].e;
			position[col]++;							//表示该列的下一个非零元素
		}
	}
}

1.3 完整实现代码

# include<stdio.h>
# define MAXSIZE 1000				//设非零元素的个数最多为1000

/*三元组*/
/*三元组的存储结构*/
typedef struct {
	int row, col;					//该非零元素的行下标和列下标
	int e;							//该非零元素的值
}Triple;
/*三元组表的存储结构*/
typedef struct {
	Triple data[MAXSIZE + 1];		//非零元素的三元组表
	int m, n, len;					//矩阵的行数、列数和非零元素的个数
}TSMatrix;

/*根据数组创建三元组表*/
void CreateTSMatrix(TSMatrix* A, int arry[][7], int m, int n) {
	int i, j, k = 1;
	for (i = 0; i < m; i++) {
		for (j = 0; j < n; j++) {
			if (arry[i][j] != 0) {
				A->data[k].row = i + 1;
				A->data[k].col = j + 1;
				A->data[k].e = arry[i][j];
				k++;
			}
		}
	}
	A->len = k - 1;
	A->m = m;
	A->n = n;
}

/*转置：列序递增转置法*/
void TransposeTSMatrix(TSMatrix* A, TSMatrix* B) {
	int i, j, k;
	B->m = A->n;
	B->n = A->m;
	B->len = A->len;
	if (B->len > 0) {
		j = 1;											//记录转置后的三元组在三元组表B中的下标值
		for (k = 1; k <= A->n; k++) {
			for (i = 1; i < A->len; i++) {				//从头至尾扫描三元组表A，寻找col值为k的三元组进行转置
				if (A->data[i].col == k) {
					B->data[j].row = A->data[i].col;
					B->data[j].col = A->data[i].row;
					B->data[j].e = A->data[i].e;
					j++;
				}
			}
		}
	}
}

/*一次定位快速转置法*/
/* num[col]用来存放三元组表A第col列中非零元素总个数
   position[col]用来存放转置前三元组表A中第col列中第一个非零元素在三元组表B中的存储位置（下标值）
   position[col]=position[col-1]+num[col-1]（col>1） */
void FastTransposeTSMatrix(TSMatrix* A, TSMatrix* B) {
	int col, t, p, q;
	int num[MAXSIZE], position[MAXSIZE];
	B->m = A->n;
	B->n = A->m;
	B->len = A->len;
	if (B->len) {
		for (col = 1; col <= A->n; col++)				//初始化num数组
			num[col] = 0;
		for (t = 1; t <= A->len; t++)
			num[A->data[t].col]++;						//扫描三元组表A，求num数组
		position[1] = 1;
		for (col = 2; col < A->n; col++)				//根据num数组求position数组
			position[col] = position[col - 1] + num[col - 1];

		for (p = 1; p <= A->len; p++) {					//扫描三元组表A，实现转置
			col = A->data[p].col;
			q = position[col];
			B->data[q].row = A->data[p].col;
			B->data[q].col = A->data[p].row;
			B->data[q].e = A->data[p].e;
			position[col]++;							//表示该列的下一个非零元素
		}
	}
}

/*根据三元组表输出稀疏矩阵*/
void Display(TSMatrix* A) {
	int i, j, k = 1;
	for (i = 1; i <= A->m; i++) {
		for (j = 1; j <= A->n; j++) {
			if (i == A->data[k].row && j == A->data[k].col) {
				printf("%3d", A->data[k].e);
				k++;
			}
			else
				printf("  0");
		}
		printf("\n");
	}
}

int main() {
	int M[6][7] = { {0,12,9,0,0,0,0},
				{0,0,0,0,0,0,0},
				{-3,0,0,0,0,14,0},
				{0,0,24,0,0,0,0},
				{0,18,0,0,0,0,0},
				{15,0,0,-7,0,0,0} };
	TSMatrix A, B, C;
	CreateTSMatrix(&A, M, 6, 7);
	TransposeTSMatrix(&A, &B);
	printf("列序递增转置法：\n");
	Display(&B);
	FastTransposeTSMatrix(&A, &C);
	printf("\n一次定位快速转置法：\n");
	Display(&C);
	return 0;
}

1.4 运行结果

【数据结构】稀疏矩阵的压缩存储（三元组表、十字链表）（C语言）

2. 十字链表

2.1 十字链表的存储结构

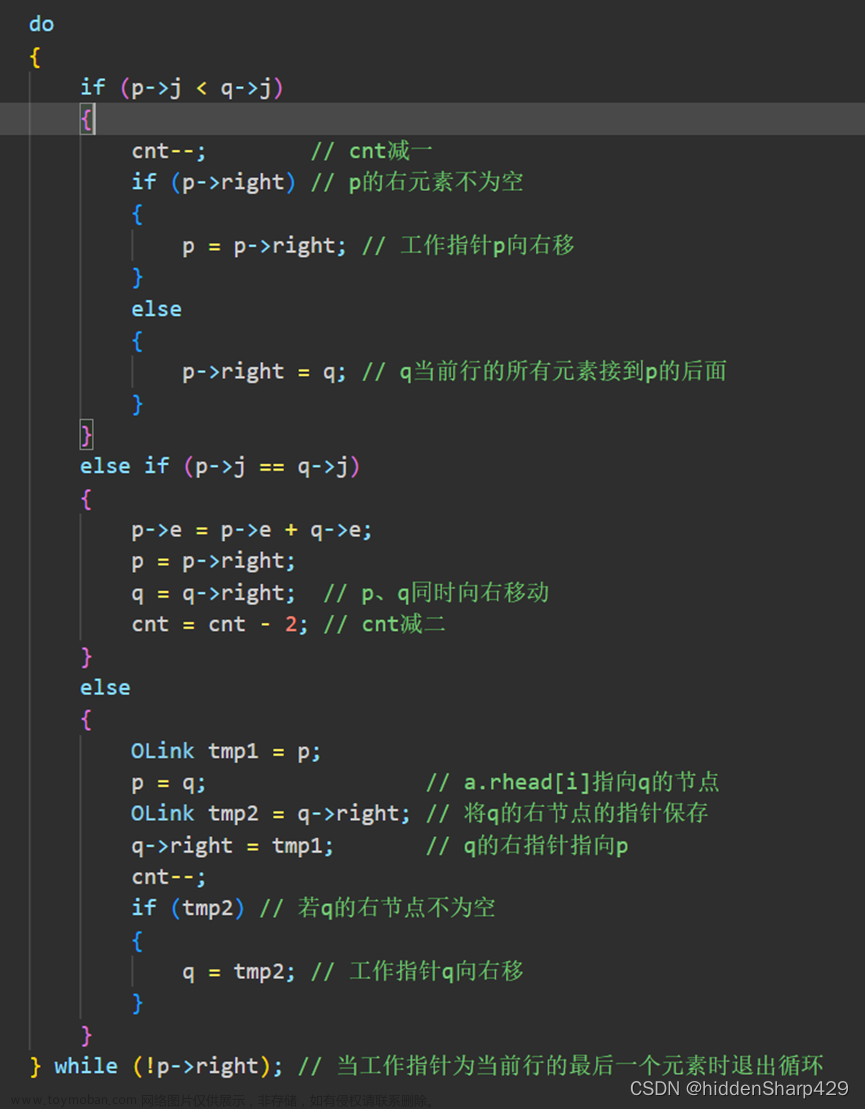
十字链表是稀疏矩阵的链式存储法。矩阵的每一个非零元素用一个结点表示，该结点除了（row，col，vaule）以外，还要添加两个链域：right 用于链接同一行中的下一个非零元素，down 用于链接同一列中的下一个非零元素。
【数据结构】稀疏矩阵的压缩存储（三元组表、十字链表）（C语言） 代码实现

/*十字链表的存储结构*/
typedef struct OLNode {
	int row, col;						//非零元素的行和列下标
	int vaule;
	struct OLNode* right, * down;		//非零元素所在行表、列表的后继链域
}OLNode, *OLink;

typedef struct {
	OLink* row_head, * col_head;		//行、列链表的头指针向量
	int m, n, len;						//稀疏矩阵的行数、列数、非零元素个数
}CrossList;

参考：耿国华《数据结构——用C语言描述（第二版）》

更多数据结构内容关注我的《数据结构》专栏：https://blog.csdn.net/weixin_51450101/category_11514538.html?spm=1001.2014.3001.5482文章来源地址https://www.toymoban.com/news/detail-414982.html

到了这里，关于【数据结构】稀疏矩阵的压缩存储（三元组表、十字链表）（C语言）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！