C++实现循环队列的算法+步骤(附全代码):
使用c++完成数据结构循环队列的基本操作,包括(初始化、入队、出队、取队头元素、遍历输出队列、求队列长度等),可直接编译运行。
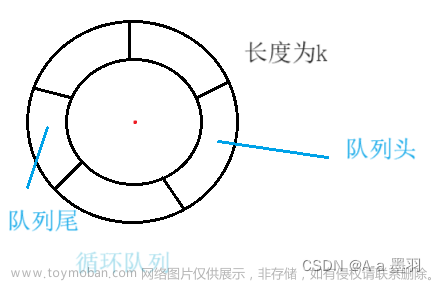
队列又称为 “先进先出” (FIFO)线性表。限定插入操作只能在队尾进行,而删除操作只能在队首进行。循环队列——采用顺序存储结构来实现,用一组连续的存储单元依次存放从队首到队尾的元素,附设两个整型变量front和rear分别指向队首元素和队尾元素的位置。
循环队列的定义:
#define MAXQSIZE 100
typedef int QElemType;
typedef int Status;
//队列的顺序存储结构
typedef struct
{
QElemType* base; //存储空间的基地址
int front; //头指针
int rear; //尾指针
}SqQueue;
循环队列的初始化:
【算法步骤】
① 为队列分配一个最大容量为MAXQSIZE的数组空间,base指向数组空间首地址。
② 头指针和尾指针置为零,表示队列为空。
【算法描述】
//循环队列的初始化
Status InitQueue(SqQueue& Q)
{//构造一个空队列Q
Q.base = new QElemType[MAXQSIZE];
if(!Q.base)
exit(OVERFLOW); //存储分配失败
Q.front = Q.rear = 0;
return OK;
}
循环队列的入队:
【算法步骤】
① 判断队列是否满,满则返回ERROR。
② 将新元素插入队尾。
③ 队尾指针加1。
【算法描述】
//循环队列的入队
Status EnQueue(SqQueue& Q, QElemType e)
{//插入元素e为Q的新的队尾元素
if ((Q.rear + 1) % MAXQSIZE == Q.front)
return ERROR; //尾指针在循环意义上加1后等于头指针,表明队满
Q.base[Q.rear] = e;
Q.rear = (Q.rear + 1) % MAXQSIZE;
return OK;
}
循环队列的出队:
【算法步骤】
① 判断队列是否为空,若空则返回ERROR。
② 保存队头元素。
③ 队头指针加1。
【算法描述】
//循环队列的出队
Status DeQueue(SqQueue& Q, QElemType &e)
{//删除Q的队头元素,用e返回其值
if (Q.front == Q.rear)
return ERROR;
e = Q.base[Q.front];
Q.front = (Q.front + 1) % MAXQSIZE;
return OK;
}
取循环队列的队头元素:
【算法步骤】
① 判断队列是否空。
② 返回队头元素的值,队头指针不变。
【算法描述】
//取循环队列的队头元素
Status GetHead(SqQueue Q)
{//返回Q的队头元素,不修改队头指针
if (Q.front != Q.rear) //队列非空
return Q.base[Q.front]; //返回队头元素的值,队头指针不变
}
取循环队列的队头元素:
【算法步骤】
① 判断队列是否空,若空则返回ERROR。
② 循环输出队头元素。
【算法描述】
//遍历输出循环队列
Status QueueTraverse(SqQueue Q)
{
cout << "当前队列为:";
if (Q.front == Q.rear)
return ERROR;
while (Q.front != Q.rear) //队列非空
{
cout << Q.base[Q.front] << " ";
Q.front = (Q.front + 1) % MAXQSIZE;
}
cout << endl;
}
求循环队列长度:
【算法描述】
//求循环队列长度
Status QueueLength(SqQueue Q)
{//返回Q的元素个数
int len = (Q.rear - Q.front + MAXQSIZE) % MAXQSIZE;
cout << "循环队列的长度为:" << len << endl;
return OK;
}
全代码如下:
//循环队列的基本操作.cpp
#include<iostream>
using namespace std;
#define ERROR 0
#define OK 1
#define MAXQSIZE 100
typedef int QElemType;
typedef int Status;
//队列的顺序存储结构
typedef struct
{
QElemType* base; //存储空间的基地址
int front; //头指针
int rear; //尾指针
}SqQueue;
Status InitQueue(SqQueue&); //初始化队列
Status EnQueue(SqQueue&, QElemType); //入队
Status DeQueue(SqQueue&, QElemType &); //出队
Status GetHead(SqQueue); //取队头元素
Status QueueTraverse(SqQueue); //遍历队列
Status QueueLength(SqQueue); //队列长度
int main()
{
SqQueue S;
int e, a;
if (InitQueue(S))
cout << "循环队列初始化成功!" << endl;
else
cout << "循环队列初始化失败!" << endl;
while (1)
{
cout << "\n【1】入队 【2】出队 【3】取队头元素 【4】输出队列 【5】求队列长度 【0】退出" << endl;
cout << "请选择要进行的操作:";
cin >> a;
switch (a)
{
case 1:
int x, n;
cout << "请输入要插入的元素个数:";
cin >> n;
for (int i = 0; i < n; i++)
{
cout << "请输入第" << i + 1 << "元素值:";
cin >> x;
EnQueue(S, x);
}
cout << "入队完成!" << endl;
break;
case 2:
cout << "请输入要删除的元素个数:";
cin >> n;
for (int j = 0; j < n; j++) {
if (!DeQueue(S, e))
cout << "出队失败!" << endl;
else
cout << "第【" << j+1 << "】个元素:" << e << " 出队成功!" << endl;
}
break;
case 3:
cout << "队头元素为:" << GetHead(S) << endl;
break;
case 4:
if(!QueueTraverse(S))
cout << "队列为空!" << endl;
break;
case 5:
QueueLength(S);
break;
case 0: return OK;
default:
return OK;
}
}
return 0;
}
//循环队列的初始化
Status InitQueue(SqQueue& Q)
{//构造一个空队列Q
Q.base = new QElemType[MAXQSIZE];
if(!Q.base)
exit(OVERFLOW); //存储分配失败
Q.front = Q.rear = 0;
return OK;
}
//循环队列的入队
Status EnQueue(SqQueue& Q, QElemType e)
{//插入元素e为Q的新的队尾元素
if ((Q.rear + 1) % MAXQSIZE == Q.front)
return ERROR; //尾指针在循环意义上加1后等于头指针,表明队满
Q.base[Q.rear] = e;
Q.rear = (Q.rear + 1) % MAXQSIZE;
return OK;
}
//循环队列的出队
Status DeQueue(SqQueue& Q, QElemType &e)
{//删除Q的队头元素,用e返回其值
if (Q.front == Q.rear)
return ERROR;
e = Q.base[Q.front];
Q.front = (Q.front + 1) % MAXQSIZE;
return OK;
}
//取循环队列的队头元素
Status GetHead(SqQueue Q)
{//返回Q的队头元素,不修改队头指针
if (Q.front != Q.rear) //队列非空
return Q.base[Q.front]; //返回队头元素的值,队头指针不变
}
//遍历输出循环队列
Status QueueTraverse(SqQueue Q)
{
cout << "当前队列为:";
if (Q.front == Q.rear)
return ERROR;
while (Q.front != Q.rear) //队列非空
{
cout << Q.base[Q.front] << " ";
Q.front = (Q.front + 1) % MAXQSIZE;
}
cout << endl;
}
//求循环队列长度
Status QueueLength(SqQueue Q)
{//返回Q的元素个数
int len = (Q.rear - Q.front + MAXQSIZE) % MAXQSIZE;
cout << "循环队列的长度为:" << len << endl;
return OK;
}
运行结果:
 文章来源:https://www.toymoban.com/news/detail-415015.html
文章来源:https://www.toymoban.com/news/detail-415015.html
美美的解决!文章来源地址https://www.toymoban.com/news/detail-415015.html
到了这里,关于【C++】【数据结构】循环队列的基本操作(初始化、入队、出队、取队头元素、遍历输出队列、求队列长度)顺序队列的算法实现【附全代码】的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!