智能优化算法：卷积优化算法-2023 附代码

智能优化算法：卷积优化算法 2023

摘要：将二维卷积运算引入智能优化算法的种群位置更新过程,提出一种新的智能优化算法,即卷积优化算法(Convolution Optimization Algorithm,COA)。 该算法主要包括卷积搜索和解质量增强 2 种机制:在卷积搜索过程中,分别定义纵向卷积核、横向卷积核和区域卷积核,依次进行二维卷积运算并更新种群的位置向量,然后将 3 种卷积核更新后的种群的位置向量进行随机权重或等比例权重相加,进一步更新种群的位置向量;在解质量增强过程中,对最优解的搜索空间逐维进行带非惯性权重的高斯变异,并对最优解进行扰动,从而提高算法的局部搜索能力。

1.卷积优化算法

COA 主要包括卷积搜索和解质量增强 2 种机制,其中:卷积搜索机制的是通过矩阵卷积运算增强搜索趋势并加快收敛速度,从而在搜索空间中获得更好的位置;解质量增强机制通过提高解的质量,避免每次迭代中出现局部最优。

1.1 种群初始化

在 $\mathrm{COA}$ 中, 个体的位置向量 ${\mathbf{X}}_p(p=1,2,\cdots$, $n$ ) 为优化问题的候选解, 定义 ${\mathbf{X}}_p$ 用于在 $d$ 维空间 中搜索,其中 $d$ 为决策变量的维度。这样, 在卷积 优化算法中, 种群的位置向量 $\mathbf{X}$ 由维度为 $d$ 的 $n$ 个个体组成, 则种群的位置向量 $\mathbf{X}$ 由 $n\times d$ 阶矩阵 构成,有
X = [ X 1 ⋮ X n ] = [ x 11 ⋯ x 1 d ⋮ ⋮ x n 1 ⋯ x n d ] (1) \boldsymbol{X}=\left[\begin{array}{c} \boldsymbol{X}_1 \\ \vdots \\ \boldsymbol{X}_n \end{array}\right]=\left[\begin{array}{ccc} x_{11} & \cdots & x_{1 d} \\ \vdots & & \vdots \\ x_{n 1} & \cdots & x_{n d} \end{array}\right] \tag{1} X= ​X1​⋮Xn​​ ​= ​x11​⋮xn1​​⋯⋯​x1d​⋮xnd​​ ​(1)
在 $\mathrm{COA}$ 中, 种群的位置向量 $X$ 的适应度值为
F X = [ f ( X 1 ) ⋮ f ( X n ) ] = [ f ( [ x 11 x 12 ⋯ x 1 d ] ) ⋮ f ( [ x n 1 x n 2 ⋯ x n d ] ) ] (2) \boldsymbol{F}_X=\left[\begin{array}{c} f\left(\boldsymbol{X}_1\right) \\ \vdots \\ f\left(\boldsymbol{X}_n\right) \end{array}\right]=\left[\begin{array}{rrrr} f\left(\left[\begin{array}{rrrr} x_{11} & x_{12} & \cdots & x_{1 d} \end{array}\right]\right) \\ & \vdots & & \\ f\left(\left[\begin{array}{rrrr} x_{n 1} & x_{n 2} & \cdots & x_{n d} \end{array}\right]\right) \end{array}\right]\tag{2} FX​= ​f(X1​)⋮f(Xn​)​ ​= ​f([x11​​x12​​⋯​x1d​​])f([xn1​​xn2​​⋯​xnd​​])​⋮​​​ ​(2)
式中: $f\left({\mathbf{X}}_p\right)$ 表示适应度函数, 也称目标函数。
在 $\mathrm{COA}$ 中,初始种群的位置向量 ${\mathbf{X}}^0$ 在 $d$ 维搜 索空间中随机生成, 每个个体的位置向量 ${\mathbf{X}}_p^0$ 的初始 化可定义为
$${\mathbf{X}}_p^0={\mathbf{l}}_p+\mathrm{rand}\cdot \left({\mathbf{u}}_p,{\mathbf{l}}_p\right)\text{\hspace{1em}(3)}$$
式中: ${\mathbf{l}}_p$ 为一个 $1\times d$ 阶矩阵, 为第 $p$ 个个体的下限; ${\mathbf{u}}_p$ 为一个 $1\times d$ 阶矩阵, 为第 $p$ 个个体的上限; rand 为 $[0,1]$ 之间的随机数。

1.2 卷积搜索机制

卷积搜索过程分为纵向卷积位置更新、横向卷积位置更新、区域卷积位置更新和综合位置更新 4个步骤。

1.2.1 纵向卷积位置更新

定义纵向卷积核为
$${\mathbf{K}}_{\mathrm{L}}=2\times \mathrm{rand}(k,1)-{\mathbf{I}}_{\mathrm{L}}\text{\hspace{1em}(4)}$$
式中: ${\mathbf{K}}_{\mathrm{L}}$ 为一个 $k\times 1$ 阶矩阵, 为纵向卷积核, 其中 $k$ 为纵向卷积核的高, 1 为纵向卷积核的宽; $\mathrm{rand}(k,1)$ 为一个 $k\times 1$ 阶矩阵,每个元素为 $[0,1]$ 之间的随机 数; ${\mathbf{I}}_{\mathrm{L}}$ 为一个 $k\times 1$ 阶矩阵, 所有元素为 1 。 定义纵向卷积为
$${\mathbf{X}}_{\mathrm{L}}^t={\mathbf{X}}^t\ast {\mathbf{K}}_{\mathrm{L}}\text{\hspace{1em}(5)}$$
式中: $t$ 为当前迭代次数; $X^t$ 为一个 $n\times d$ 阶矩阵, 为 第 $t$ 代种群的位置向量; $X_{\mathrm{L}}^t$ 为一个 $n\times d$ 阶矩阵, 为 第 $t$ 代纵向卷积位置更新后的种群的位置向量。
比较 ${\mathbf{X}}_{\mathrm{L}}^t$ 和 ${\mathbf{X}}^t$ 中每个个体位置的适应度值的大 小,择优替换掉 ${\mathbf{X}}^t$ 中个体位置, 则有
$${\mathbf{X}}_p^t=\{\begin{array}{l}{\mathbf{X}}_{\mathrm{Lp}}^t,f\left({\mathbf{X}}_{\mathrm{Lp}}^t\right)<f\left({\mathbf{X}}_p^t\right);\\ {\mathbf{X}}_p^t,\text{ else }。\end{array}\text{\hspace{1em}(6)}$$
式中: ${\mathbf{X}}_p^t$ 为第 $t$ 代种群的第 $p$ 个个体位置; ${\mathbf{X}}_{\mathrm{L}p}^t$ 为 第 $t$ 代纵向卷积位置更新后的种群的第 $p$ 个个体 位置。

1.2.2 横向卷积位置更新

定义横向卷积核为
$${\mathbf{K}}_{\mathrm{T}}=2\times \mathrm{rand}(k,1)-{\mathbf{I}}_{\mathrm{T}}\text{\hspace{1em}(7)}$$
式中: ${\mathbf{K}}_{\mathrm{T}}$ 为一个 $1\times k$ 阶矩阵, 为横向卷积核, 其中 1 为横向卷积核的高, $k$ 为横向卷积核的宽; $\mathrm{rand}(1,k)$ 为一个 $1\times k$ 阶矩阵,每个元素为 $[0,1]$ 之间的随机 数; ${\mathbf{I}}_{\mathrm{T}}$ 为一个 $1\times k$ 阶矩阵,所有元素为 1 。
定义横向卷积为
$${\mathbf{X}}_{\mathrm{T}}^t={\mathbf{X}}^t\ast {\mathbf{K}}_{\mathrm{T}}\text{\hspace{1em}(8)}$$
式中: ${\mathbf{X}}_{\mathrm{T}}^t$ 为一个 $n\times d$ 阶矩阵, 为横向卷积更新后的 种群的位置向量。
比较 ${\mathbf{X}}_{\mathrm{T}}^t$ 和 ${\mathbf{X}}^t$ 中每个个体位置的适应度值的大 小,择优替换掉 ${\mathbf{X}}^t$ 中个体位置,则有
$${\mathbf{X}}_p^t=\{\begin{array}{l}{\mathbf{X}}_{{\mathrm{T}}_p}^t,f\left({\mathbf{X}}_{{\mathrm{T}}_p}^t\right)<f\left({\mathbf{X}}_p^t\right);\\ {\mathbf{X}}_p^t,\text{ else }\end{array}\text{\hspace{1em}(9)}$$
式中: $X_{{\mathrm{T}}_p}^t$ 为第 $t$ 代横向卷积位置更新后的种群的第$p$ 个个体位置。

1.2.3 区域卷积位置更新

定义区域卷积核为
$${\mathbf{K}}_{\mathrm{R}}=2\times \mathrm{rand}(k,1)-{\mathbf{I}}_{\mathrm{R}}\text{\hspace{1em}(10)}$$
式中: ${\mathbf{K}}_{\mathrm{R}}$ 为一个 $k\times k$ 阶矩阵, 为区域卷积核, 其中 $k$ 为区域卷积核的高和宽; $\mathrm{rand}(k,k)$ 为一个 $k\times k$ 阶 矩阵,每个元素为 $[0,1]$ 之间的随机数; ${\mathbf{I}}_{\mathrm{R}}$ 为一个 $k\times k$ 阶矩阵,所有元素为 1 。
定义区域卷积为
$${\mathbf{X}}_{\mathrm{R}}^t={\mathbf{X}}^t\ast {\mathbf{K}}_{\mathrm{R}}\text{\hspace{1em}(11)}$$
式中: ${\mathbf{X}}_{\mathrm{R}}^t$ 为一个 $n\times d$ 阶矩阵, 为区域卷积更新后的 种群的位置向量。
比较 ${\mathbf{X}}_{\mathrm{R}}^t$ 和 ${\mathbf{X}}^t$ 中每个个体位置的适应度值的大 小,择优替换掉 $X^t$ 中个体位置, 则有
$${\mathbf{X}}_p^t=\{\begin{array}{l}{\mathbf{X}}_{\mathrm{R}p}^t,f\left({\mathbf{X}}_{\mathrm{R}p}^t\right)<f\left({\mathbf{X}}_p^t\right);\\ {\mathbf{X}}_p^t,\text{ else }\end{array}\text{\hspace{1em}(12)}$$
式中: $X_{\mathrm{R}p}^t$ 为第 $t$ 代区域卷积位置更新后的种群的第 $p$ 个个体位置。

1.2.4 综合位置更新

在综合位置更新阶段, 将第 $t$ 代纵向卷积更新 后的种群的位置向量 $X_{\mathrm{L}}^t$, 第 $t$ 代横向卷积更新后的 种群的位置向量 $X_{\mathrm{T}}^t$ 和第 $t$ 代区域卷积更新后的种 群的位置向量 ${\mathbf{X}}_{\mathrm{R}}^t$, 采用随机权重或等比例权重相加 合并为 ${\mathbf{X}}_{\mathrm{s}}^t$, 即
$${\mathbf{X}}_{\mathrm{S}}^t=\frac{r_1\times {\mathbf{X}}_{\mathrm{L}}^t+r_2\times {\mathbf{X}}_{\mathrm{T}}^t+r_3\times {\mathbf{X}}_{\mathrm{R}}^t}{r_1+r_2+r_3}\text{\hspace{1em}(13)}$$
式中: $r_1、r_2、r_3$ 均为 $[0,1]$ 之间的随机数, 特别地, 可 以令 $r_1=r_2=r_3$, 以便进行等比例权重相加。
比较 ${\mathbf{X}}_{\mathrm{s}}^t$ 和 ${\mathbf{X}}^t$ 中每个个体位置的适应度值的大 小,择优替换掉 $X^t$ 中个体位置, 则有
$${\mathbf{X}}_p^t=\{\begin{array}{l}{\mathbf{X}}_{\mathrm{sp}}^t,f\left({\mathbf{X}}_{\mathrm{spp}}^t\right)<f\left({\mathbf{X}}_p^t\right);\\ {\mathbf{X}}_p^t,\text{ else }\end{array}\text{\hspace{1em}(14)}$$
式中: $X_{\mathrm{s}p}^t$ 为第 $t$ 代综合位置更新后的种群的第 $p$ 个 个体位置。
最后, 计算 ${\mathbf{X}}^t$ 中所有个体位置的适应度值, 并根据适应度值的大小进行排序, 选出最优 解 ${\mathbf{X}}_{\mathrm{bs}}^t$ 。

1.3 解质量增强机制

在 $\mathrm{COA}$ 中,解质量增强机制是对最优解 ${\mathbf{X}}_{\mathrm{bs}}^t$ 的 $d$ 维搜索空间逐维进行带非惯性权重的高斯变异, 对最优解 ${\mathbf{X}}_{\mathrm{bs}}^t$ 进行扰动, 从而提高算法的局部搜 索能力。
对最优解 ${\mathbf{X}}_{\mathrm{bs}}^t$ 中 $d$ 维搜索空间逐维进行带非惯性权重的高斯变异, 则有
$${\mathbf{X}}_{\mathrm{nbs}(q)}^t=\omega \cdot {\mathbf{X}}_q^t+\mathrm{randn}\cdot {\mathbf{X}}_{\mathrm{bs}(q)}^t\text{\hspace{1em}(15)}$$
式中: ${\mathbf{X}}_{\mathrm{bs}(q)}^t={\left[\begin{array}{llll}{x}_{1q}& x_{2q}& \cdots & x_{nq}\end{array}\right]}^{\mathrm{T}}$ 为一个 $n\times 1$ 阶 矩阵, 为最优解 ${\mathbf{X}}_{\mathrm{bs}}^t$ 中 $d$ 维搜索空间中的第 $q(q=1$, $2,\cdots ,d)$ 维的位置; $\omega =1-{\left(t/{\text{ iter }}_{\text{max }}\right)}^2$, 其中 iter ${}_{\text{max }}$ 为最大迭代次数; randn 为一个满足均值为 0 , 方差 为 1 的标准正态分布的随机数; $X_{\mathrm{nbs}(q)}^t$ 为一个 $n\times 1$ 阶矩阵, 为对最优解 ${\mathbf{X}}_{\mathrm{bs}}^t$ 的第 $q$ 维进行带非惯性权重 高斯变异后的第 $q$ 维位置。
令对第 $q$ 维进行带非惯性权重高斯变异后的个 体位置为 ${\mathbf{X}}_{(q)\text{ nbs }}^t$, 比较 ${\mathbf{X}}_{(q)\text{ nbs }}^t$ 和 ${\mathbf{X}}_{\mathrm{bs}}^t$ 的适应度值的大 小,择优替换掉 $X_{\mathrm{bs}}^t$ 的个体位置,则有
$${\mathbf{X}}_{\mathrm{bs}}^t=\{\begin{array}{ll}{\mathbf{X}}_{(q)\mathrm{nbs}}^t,& f\left({\mathbf{X}}_{(q)\mathrm{nbs}}^t\right)<f\left({\mathbf{X}}_{\mathrm{bs}}^t\right);\\ {\mathbf{X}}_{\mathrm{bs}}^t,& \text{ else }。\end{array}\text{\hspace{1em}(16)}$$
$\mathrm{COA}$ 运行过程的伪代码如下:
输人: 种群大小为 $n$, 个体位置的维度为 $d$, 最大 迭代次数为 iter ${}_{\text{max }}$, 卷积核参数为 $k$ 和适应度函数为 $f\left({\mathbf{X}}_p\right)(p=1,2,\cdots ,n)$
输出:最优解及其位置
1 : 初始化种群, 计算每个个体位置的适应度值, 选出最优个体的适应度值及其位置
2 : While $t⩽$ iter ${}_{\text{max }}$ do
3 : 在纵向卷积位置更新阶段, 由式 (4)- (6) 更 新种群的位置向量
4 : 在横向卷积位置更新阶段, 由式 (7)- (9) 更 新种群的位置向量
5 : 在区域卷积位置更新阶段, 由式 (10)-(12) 更新种群的位置向量
6 : 在综合位置更新阶段, 由式 (13)、(14) 更新 种群的位置向量
7 : 计算种群个体位置的适应度值, 选出最优解
8 : for $q=1$ to $d$ do
9 : 在解增强阶段, 由式 (15)、(16) 更新最优解 及其位置
10 : end for
11 : 更新全局最优解及其位置
$12:t=t+1$
13 : end while

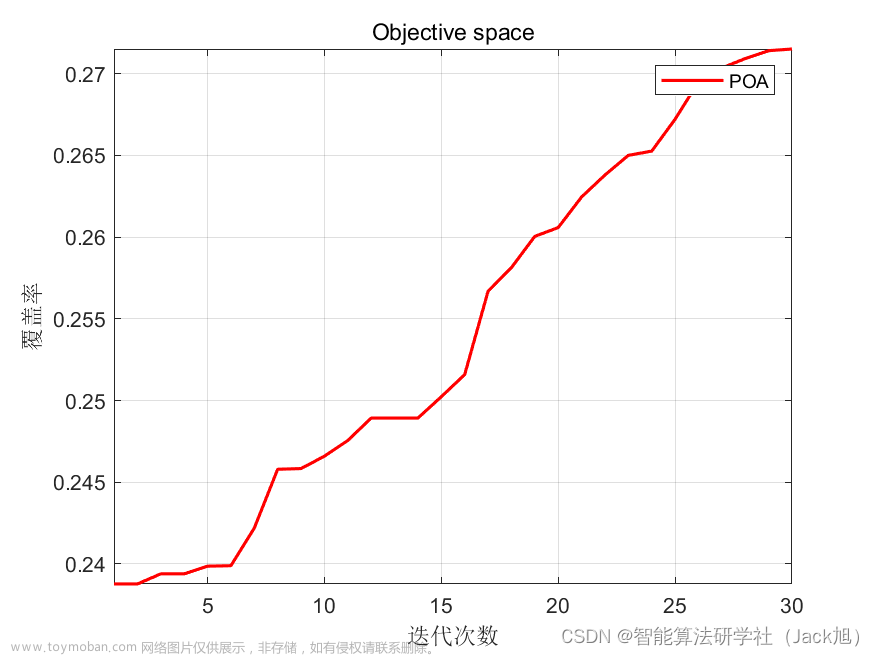
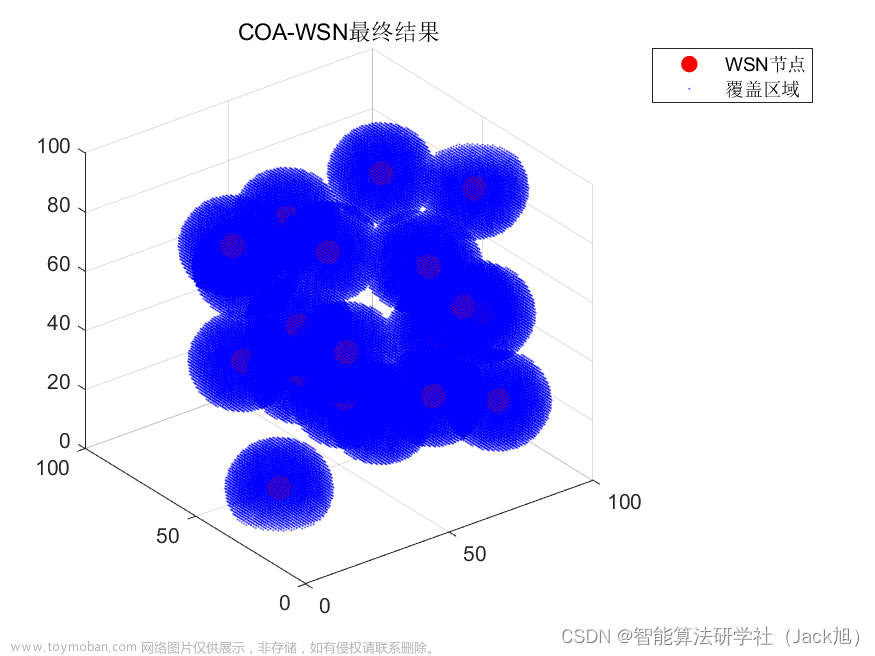
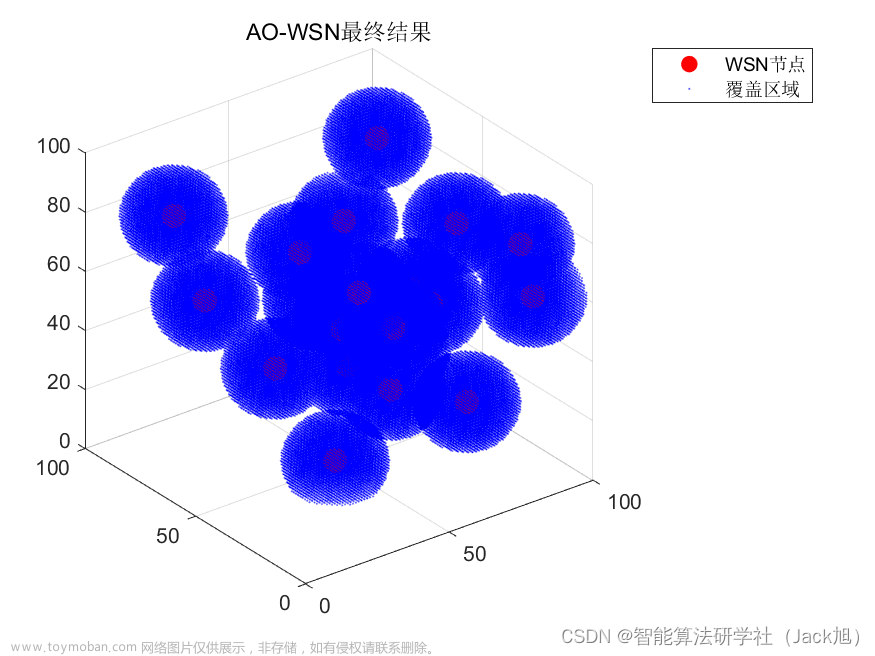
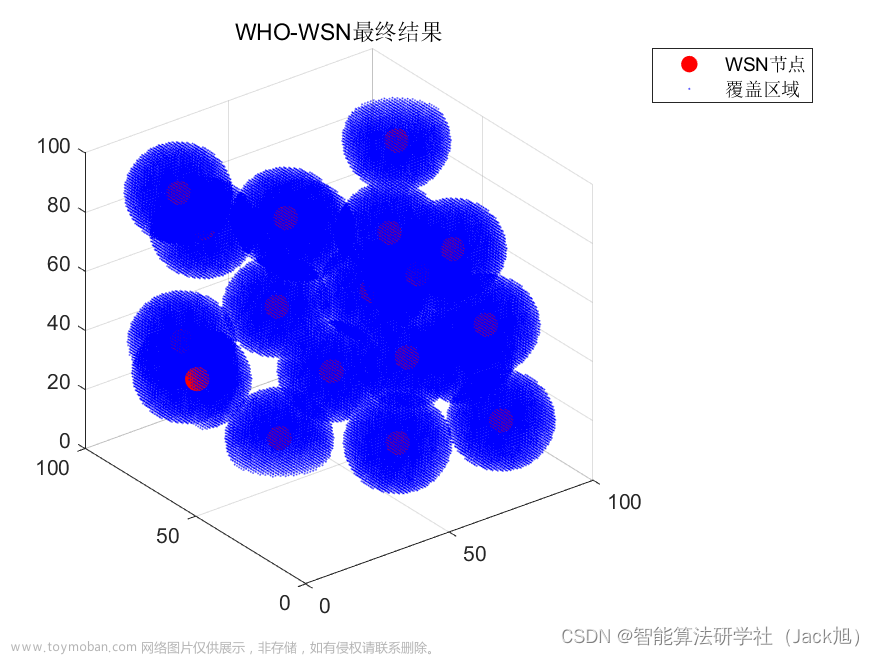
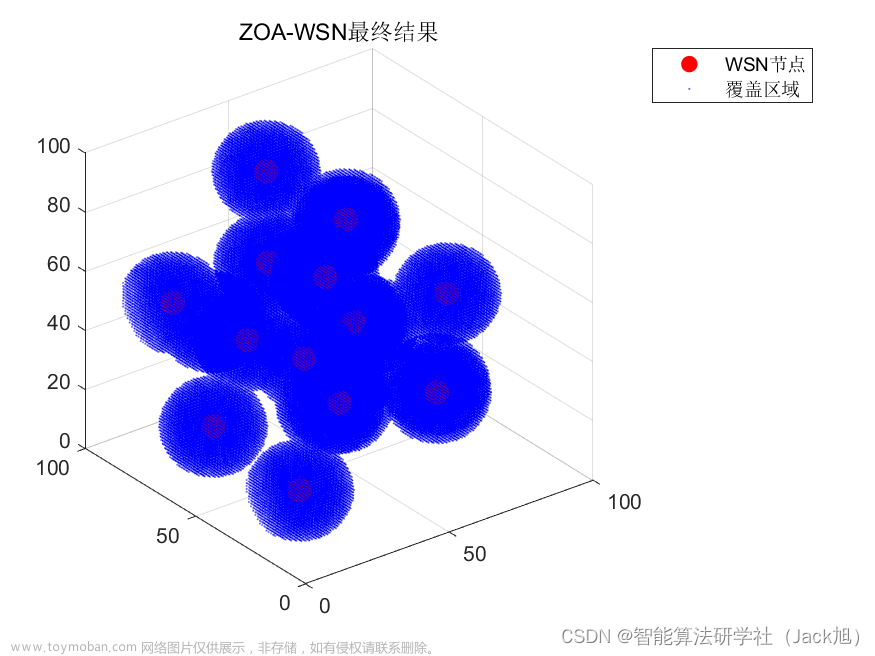
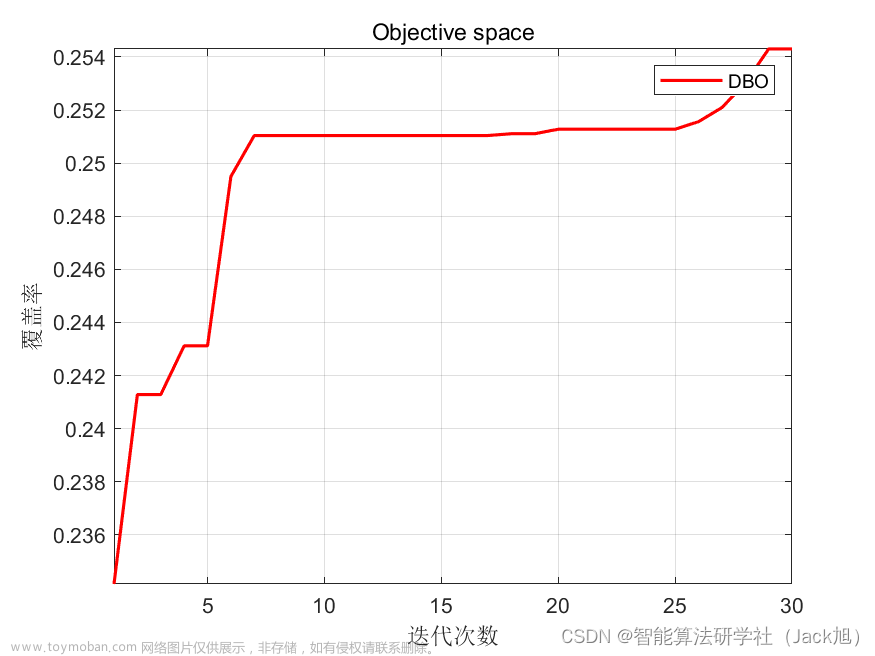
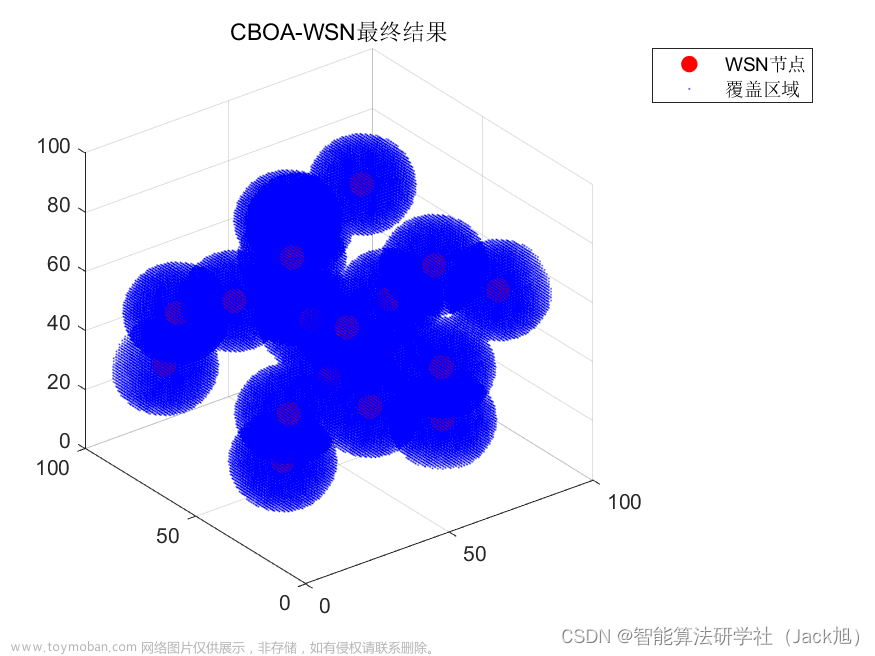
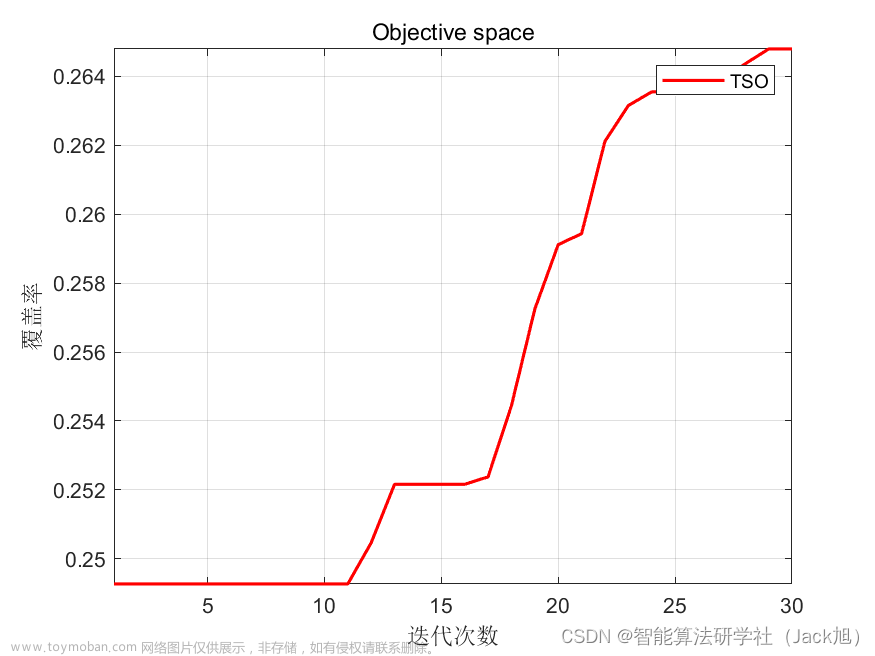
2.实验结果

3.参考文献

[1]陈克伟,魏曙光,张嘉曦.基于二维卷积运算的智能优化算法[J].装甲兵学报,2023,2(01):102-108.文章来源地址https://www.toymoban.com/news/detail-415174.html

4.Matlab

5.Python

到了这里，关于智能优化算法：卷积优化算法-2023 附代码的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！