基于TSP(旅行商)问题的混合粒子群算法附直接运行代码-Toy模板网

这篇具有很好参考价值的文章主要介绍了基于TSP(旅行商)问题的混合粒子群算法附直接运行代码。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

如果对粒子群一点都不知道的可以看看上文标准粒子群算法，想看代码的直接去下面1.4标题即可

链接：(105条消息) 自己对粒子群算法的理解（附matlab直接运行代码)(二维)_吕浩轩的博客-CSDN博客_二维粒子群算法h

好现在开始正文：

1.1 前言：理论基础

标准粒子群通过追随个体极值和群体极值完成极值寻优，虽然简单，且能快速收敛，但是随着迭代次数的增加，在种群收敛集中的过程中，各个粒子也越来越相似(接近)，这样就有可能进入局部最优解而无法跳出。

混合粒子群算法：摈弃了传统粒子群算法中的通过追踪极值来更新粒子位置的方法，引入了遗传算法中的交叉和变异操作，通过粒子同个体极值和群体极值的交叉以及粒子自身变异的方式来搜索最优解。

1.2 算法流程

基本上和标准粒子群基本一致。（图有点糊，抱歉）

基于TSP(旅行商)问题的混合粒子群算法附直接运行代码

1.3 算法实现

1.3.1 ：个体编码

在写代码前，先要讲一下粒子的个体编码

粒子个体采用整数编码，每个粒子代表经过的城市，比如A粒子=5，A的个体编码为[2 5 1 3 6]

表示城市遍历从2开始，途径 5 1 3 6到2结束，没错，是返回2了。这样才能完成TSP的遍历。

1.3.2 ：适应度值

粒子适应度值就是遍历路径的长度，计算公式为如下：

基于TSP(旅行商)问题的混合粒子群算法附直接运行代码

n为城市数量，path（i，j）为城市i，j之间的路径长度

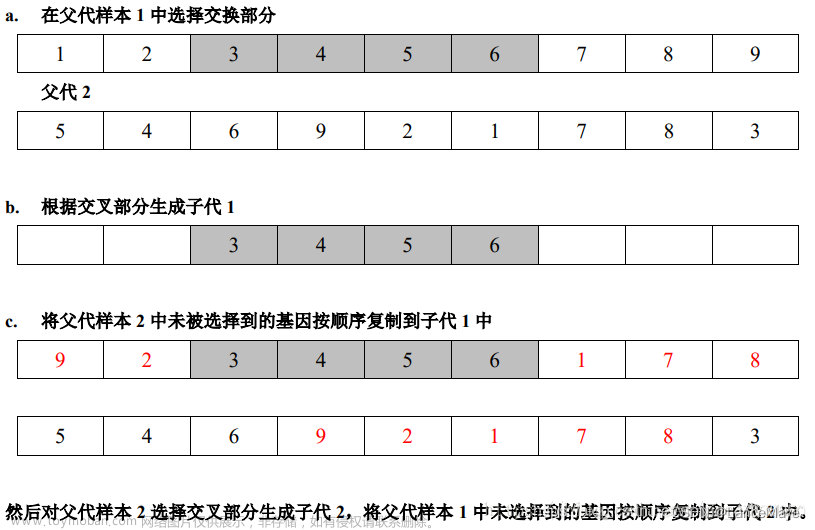
1.3.3：交叉操作

交叉操作
个体通过个体极值和群体极值交叉来更新，交叉方法采用整数交叉法。首先选择两个交叉位置，然后把个体和个体极值或个体与群体极值进行交叉，假定随机选取的交叉位置为3和4位置，操作方法如下：
个体：[9 4 2 1 3 7 6 10 8 5]

极值：[9 2 1 6 3 7 4 10 8 5]
交叉为新个体：[9 4 1 6 3 7 6 10 8 5]

在MATLAB智能算法30个案例这本书中是用上面的素材交换3和5位置生成[9 4 1 6 3 7 6 10 8 5]，我个人感觉可能是把3 4 写成了 3 5位置，或者可能是我理解问题，不过这个关系不大，毕竟交叉是随机的

产生的新个体如果存在重复位置则进行调整，调整方法为用个体中未包括的城市代替重复包括的城市，如下所示：
[9 4 1 6 3 7 6 10 8 5]

调整为：[9 4 2 1 3 7 6 10 8 5] (之前个体中2没有被包括进来，所以用2来代替出现了两次的6)
对得到的新个体采用了保留优秀个体策略，只有当新粒子适应度值好于旧粒子时才更新粒子。

1.3.4：变异操作

编译方法采用个体内部自己两位互换，随机选择两个变异位置，下面举个例子：

[9 4 2 1 3 7 6 10 8 5] 将 pos1 = 2和pos1 = 5互换

变异成 [9 3 2 1 4 7 6 10 8 5]

当然，对新得到的个体采用保留优秀个体的策略，只有当新的粒子适应度值好于旧粒子时才更新粒子(不然不瞎操作一大堆了)

1.4 代码实现

1.4.1 首先加载一下城市的坐标数据

cityCoor : 城市坐标

cityDist : 城市距离

x ：个体

indiFit ：个体适应度

%% 下载数据
data=load('eil51.txt');%导入城市坐标文件，后面我会提供
cityCoor=[data(:,2) data(:,3)];%城市坐标矩阵
figure
plot(cityCoor(:,1),cityCoor(:,2),'ms','LineWidth',2,'MarkerEdgeColor','k','MarkerFaceColor','r')
legend('城市位置')
ylim([4 78])
title('城市分布图','fontsize',12)
xlabel('km','fontsize',12)
ylabel('km','fontsize',12)
%ylim([min(cityCoor(:,2))-1 max(cityCoor(:,2))+1])

grid on

1.4.2 计算城市间的距离

%% 计算城市间距离
n=size(cityCoor,1);            %城市数目
cityDist=zeros(n,n);           %城市距离矩阵
for i=1:n
    for j=1:n
        if i~=j
            cityDist(i,j)=((cityCoor(i,1)-cityCoor(j,1))^2+...
                (cityCoor(i,2)-cityCoor(j,2))^2)^0.5;
        end
        cityDist(j,i)=cityDist(i,j);
    end
end
nMax=200;                      %进化次数
indiNumber=1000;               %个体数目
individual=zeros(indiNumber,n);
%^初始化粒子位置
for i=1:indiNumber
    individual(i,:)=randperm(n);    
end

1.4.3：拥有距离后计算种群的适应度

%% 计算种群适应度
indiFit=fitness(individual,cityCoor,cityDist);%个体适应度值
[value,index]=min(indiFit);                        %找到最短和其对应的下标
tourPbest=individual;                              %当前个体最优
tourGbest=individual(index,:) ;                    %当前全局最优
recordPbest=inf*ones(1,indiNumber);                %个体最优记录
recordGbest=indiFit(index);                        %群体最优记录
xnew1=individual;

1.4.4：运用循环取寻找最优的路径,同时引进交叉操作和变异操作

%% 循环寻找最优路径
L_best=zeros(1,nMax);

for N=1:nMax
    %计算适应度值
    indiFit=fitness(individual,cityCoor,cityDist);
    
    %更新当前最优和历史最优
    for i=1:indiNumber
        if indiFit(i)<recordPbest(i)
            recordPbest(i)=indiFit(i);
            tourPbest(i,:)=individual(i,:);
        end
        if indiFit(i)<recordGbest
            recordGbest=indiFit(i);
            tourGbest=individual(i,:);
        end
    end
    
    [value,index]=min(recordPbest);
    recordGbest(N)=recordPbest(index);
    
    %% 交叉操作
    for i=1:indiNumber
       % 与个体最优进行交叉
        c1=unidrnd(n-1); %产生交叉位,unidrnd可以随机产生一个固定范围内的离散数据
        c2=unidrnd(n-1); %产生交叉位
        while c1==c2
            c1=round(rand*(n-2))+1;
            c2=round(rand*(n-2))+1;
        end
        chb1=min(c1,c2);
        chb2=max(c1,c2);
        cros=tourPbest(i,chb1:chb2);
        ncros=size(cros,2);      
        %删除与交叉区域相同元素，并将个体未被包括的城市代替重复的城市
        for j=1:ncros
            for k=1:n
                if xnew1(i,k)==cros(j)
                    xnew1(i,k)=0;
                    for t=1:n-k
                        temp=xnew1(i,k+t-1);
                        xnew1(i,k+t-1)=xnew1(i,k+t);
                        xnew1(i,k+t)=temp;
                    end
                end
            end
        end
        %插入交叉区域
        xnew1(i,n-ncros+1:n)=cros;
        %新路径长度变短则接受
        dist=0;
        for j=1:n-1
            dist=dist+cityDist(xnew1(i,j),xnew1(i,j+1));
        end
        dist=dist+cityDist(xnew1(i,1),xnew1(i,n));
        if indiFit(i)>dist
            individual(i,:)=xnew1(i,:);
        end
        
        % 与全体最优进行交叉
        c1=round(rand*(n-2))+1;  %产生交叉位
        c2=round(rand*(n-2))+1;  %产生交叉位
        while c1==c2
            c1=round(rand*(n-2))+1;
            c2=round(rand*(n-2))+1;
        end
        chb1=min(c1,c2);
        chb2=max(c1,c2);
        cros=tourGbest(chb1:chb2); 
        ncros=size(cros,2);      
        %删除与交叉区域相同元素
        for j=1:ncros
            for k=1:n
                if xnew1(i,k)==cros(j)
                    xnew1(i,k)=0;
                    for t=1:n-k
                        temp=xnew1(i,k+t-1);
                        xnew1(i,k+t-1)=xnew1(i,k+t);
                        xnew1(i,k+t)=temp;
                    end
                end
            end
        end
        %插入交叉区域
        xnew1(i,n-ncros+1:n)=cros;
        %新路径长度变短则接受
        dist=0;
        for j=1:n-1
            dist=dist+cityDist(xnew1(i,j),xnew1(i,j+1));
        end
        dist=dist+cityDist(xnew1(i,1),xnew1(i,n));
        if indiFit(i)>dist
            individual(i,:)=xnew1(i,:);
        end
        
       %% 变异操作
        c1=round(rand*(n-1))+1;   %产生变异位
        c2=round(rand*(n-1))+1;   %产生变异位
        while c1==c2
            c1=round(rand*(n-2))+1;
            c2=round(rand*(n-2))+1;
        end
        temp=xnew1(i,c1);
        xnew1(i,c1)=xnew1(i,c2);
        xnew1(i,c2)=temp;
        
        %新路径长度变短则接受
        dist=0;
        for j=1:n-1
            dist=dist+cityDist(xnew1(i,j),xnew1(i,j+1));
        end
        dist=dist+cityDist(xnew1(i,1),xnew1(i,n));
        if indiFit(i)>dist
            individual(i,:)=xnew1(i,:);
        end
    end

    [value,index]=min(indiFit);
    L_best(N)=indiFit(index);
    tourGbest=individual(index,:); 
    
end

1.4.5：结果作图咯

%% 结果作图
figure
plot(L_best)
title('算法训练过程')
xlabel('迭代次数')
ylabel('适应度值')
grid on


figure
hold on
plot([cityCoor(tourGbest(1),1),cityCoor(tourGbest(n),1)],[cityCoor(tourGbest(1),2),...
    cityCoor(tourGbest(n),2)],'ms-','LineWidth',2,'MarkerEdgeColor','k','MarkerFaceColor','g')
hold on
for i=2:n
    plot([cityCoor(tourGbest(i-1),1),cityCoor(tourGbest(i),1)],[cityCoor(tourGbest(i-1),2),...
        cityCoor(tourGbest(i),2)],'ms-','LineWidth',2,'MarkerEdgeColor','k','MarkerFaceColor','g')
    hold on
end
legend('规划路径')
scatter(cityCoor(:,1),cityCoor(:,2));
title('规划路径','fontsize',10)
xlabel('km','fontsize',10)
ylabel('km','fontsize',10)

grid on
ylim([4 80])

第一组：城市共20个

基于TSP(旅行商)问题的混合粒子群算法附直接运行代码