【2023 年第十三届 MathorCup 高校数学建模挑战赛】C 题电商物流网络包裹应急调运与结构优化问题建模方案及代码实现-Toy模板网

这篇具有很好参考价值的文章主要介绍了【2023 年第十三届 MathorCup 高校数学建模挑战赛】C 题电商物流网络包裹应急调运与结构优化问题建模方案及代码实现。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

【2023 年第十三届 MathorCup 高校数学建模挑战赛】C 题电商物流网络包裹应急调运与结构优化问题

【2023 年第十三届 MathorCup 高校数学建模挑战赛】C 题电商物流网络包裹应急调运与结构优化问题建模方案及代码实现

1 题目

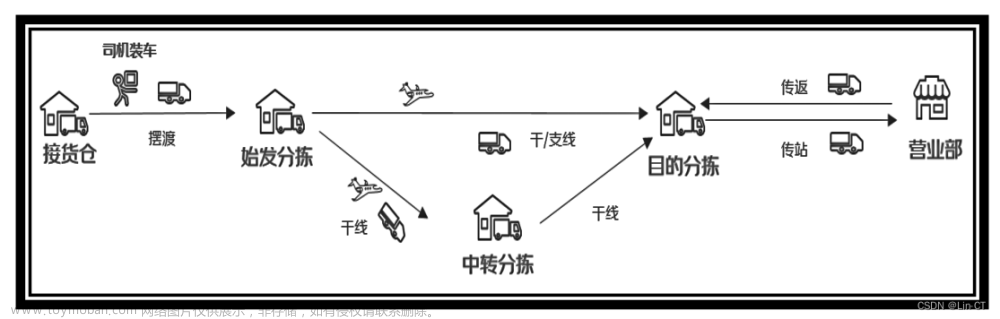
电商物流网络由物流场地（接货仓、分拣中心、营业部等）和物流场地之间的运输线路组成，如图 1 所示。受节假日和“双十一”、“618”等促销活动的影响，电商用户的下单量会发生显著波动，而疫情、地震等突发事件导致物流场地临时或永久停用时，其处理的包裹将会紧急分流到其他物流场地，这些因素均会影响到各条线路运输的包裹数量，以及各个物流场地处理的包裹数量。

【2023 年第十三届 MathorCup 高校数学建模挑战赛】C 题电商物流网络包裹应急调运与结构优化问题建模方案及代码实现

如果能预测各物流场地及线路的包裹数量（以下简称货量），管理者将可以提前安排运输、分拣等计划，从而降低运营成本，提高运营效率。特别地，在某些场地临时或永久停用时，基于预测结果和各个物流场地的处理能力及线路的运输能力，设计物流网络调整方案，将会大大降低物流场地停用对物流网络的影响，保障物流网络的正常运行。

附件 1 给出了某物流网络在 2021-01-01 至 2022-12-31 期间每天不同物流场地之间流转的货量数据，该物流网络有 81 个物流场地，1049 条线路。其中线路是有方向的，比如线路 DC1→DC2 和线路 DC2→DC1 被认为是两条线路。假设每个物流场地的处理能力和每条线路的运输能力上限均为其历史货量最大值。

基于以上背景，请你们团队完成以下问题：

问题 1：建立线路货量的预测模型，对 2023-01-01 至 2023-01-31 期间每条线路每天的货量进行预测，并在提交的论文中给出线路 DC14→DC10、DC20→DC35、DC25→DC62 的预测结果。

问题 2：如果物流场地 DC5 于 2023-01-01 开始关停，请在问题 1 的预测基础上，建立数学模型，将 DC5 相关线路的货量分配到其他线路使所有包裹尽可能正常流转，并使得 DC5 关停前后货量发生变化的线路尽可能少，且保持各条线路的工作负荷尽可能均衡。如果存在部分日期部分货量没有正常流转，你们的分流方案还应使得 2023-01-01 至 2023-01-31 期间未能正常流转的包裹日累计总量尽可能少。正常流转时，请给出因 DC5 关停导致货量发生变化的线路数及网络负荷情况；不能正常流转时，请给出因 DC5 关停导致货量发生变化的线路数、不能正常流转的货量及网络的负荷情况。

问题 3：在问题 2 中，如果被关停的物流场地为 DC9，同时允许对物流网络结构进行动态调整（每日均可调整），调整措施为关闭或新开线路，不包含新增物流场地，假设新开线路的运输能力的上限为已有线路运输能力的最大值。请将 DC9 相关线路的货量分配到其他线路，使所有包裹尽可能正常流转，并使得 DC9 关停前后货量发生变化的线路数尽可能少，且保持各条线路的工作负荷尽可能均衡。如果存在部分日期没有满足要求的流转方案，你们的分流方案还应使得 2023-01-01 至 2023-01-31 期间未能正常流转的包裹日累计总量尽可能少。正常流转时，请给出因 DC9 关停导致货量发生变化的线路数及网络负荷情况；不能正常流转时，请给出因 DC9 关停导致货量发生变化的线路数、不能正常流转的货量及网络的负荷情况；同时请给出每天的线路增减情况。

问题 4：根据附件 1，请对该网络的不同物流场地及线路的重要性进行评价；为了改善网络性能，如果打算新增物流场地及线路，结合问题 1 的预测结果，探讨分析新增物流场地应与哪几个已有物流场地之间新增线路，新增物流场地的处理能力及新增线路的运输能力应如何设置？考虑到预测结果的随机性，请进一步探讨你们所建网络的鲁棒性。

2 方案解析

2.1 问题一

针对第一个问题，我们可以采用时间序列分析方法来建立线路货量的预测模型。具体的步骤如下：

数据预处理：将附件1中的数据按照时间顺序进行排序，并将其转换为时间序列数据。
时间序列分解：对时间序列数据进行季节性、趋势性和随机性分解，以便更好地理解其内部结构。
模型选择：基于时间序列的性质和内部结构，选择适当的时间序列模型，例如ARIMA、ARIMAX等。
参数估计：利用最大似然估计方法或贝叶斯估计方法，估计所选模型的参数。
模型诊断：对所建立的模型进行诊断，检验其残差是否符合一些假设条件，例如均值为零、独立等。
模型预测：利用建立好的模型，对未来一段时间内每条线路每天的货量进行预测。

针对题目要求，需要对2023年1月1日至1月31日期间每条线路每天的货量进行预测，并给出线路DC14→DC10、DC20→DC35、DC25→DC62的预测结果。因此，需要根据附件1中的数据，建立时间序列模型，并利用该模型进行预测。

问题二

针对这个问题，需要重新调整第一问中的预测模型，将 DC5 相关线路的货量分配到其他线路，使得所有包裹尽可能正常流转，且保持各条线路的工作负荷尽可能均衡。可以考虑以下步骤：

计算 DC5 相关线路的平均每日货量，以及 DC5 关停前的天数。
将 DC5 相关线路的平均每日货量按照关停前的天数进行加权平均，得到一个平均每日需要分配的货量。
将 DC5 相关线路的货量分配到其他线路，使得所有包裹尽可能正常流转，并使得各条线路的工作负荷尽可能均衡。这个过程可以使用线性规划等数学模型进行求解。
重新预测分配后的各条线路的货量，得到 DC5 关停后的货量情况。
对于正常流转的情况，
对于不能正常流转的情况，
最后，对于不能正常流转的情况，
。。。略，请下载完整文档

需要注意的是，在以上步骤中，我们需要考虑一些约束条件，例如各条线路的工作负荷均衡、每个包裹只能被分配一次等。同时，我们也需要根据具体情况进行调整和优化，以求得最优解。

问题三

为了解决这个问题，需要对物流网络进行重新规划，以最小化对货量的影响，同时尽可能均衡线路的工作负荷。以下是一个可能的解决方案：

确定DC9关停前的货量分配情况，
将DC9的货量平均分配到其他线路上，
对于每个物流线路，
对于不能正常流转的包裹，

具体步骤如下：

。。。略，请下载完整文档

问题四

对于该物流网络的不同场地及线路的重要性评价，可以考虑以下几个因素：

交通便捷程度
场地面积及容量
。。。略，请下载完整文档

对于该网络的鲁棒性，可以考虑以下几个方面：

可扩展性：
风险控制：
多样化：
技术支持：
管理规范：

3 代码实现

% 我将附件1中的列名，全部重命名了的

% 导入时间序列分解工具包
addpath(fullfile(matlabroot,'toolbox','econ','econ'))

% site1	site	date	goods
% 读取数据文件
data = readtable('附件1：物流网络历史货量数据.xlsx');

% 对数据按照日期进行排序
data = sortrows(data, 'date');

% 将数据转换为时间序列数据
date_str = string(data.date);
date_num = datenum(date_str, 'yyyy-mm-dd');
ts_data = timeseries(data.goods, date_num);
ts_data.TimeInfo.Format = 'yyyy-mm-dd';

% 对时间序列进行季节性、趋势性和随机性分解
decomposition = decompose(ts_data,ts_data.Data, 'additive', 12);

% 绘制原始时间序列、趋势、季节和随机分量的图形
figure;
subplot(4,1,1);
plot(ts_data);
title('原始时间序列');
subplot(4,1,2);
plot(decomposition.trend);
title('趋势分量');
subplot(4,1,3);
plot(decomposition.seasonal);
title('季节分量');
subplot(4,1,4);
plot(decomposition.random);
title('随机分量');

% 选择ARIMA模型并进行参数估计
model = arima('Seasonality',12,'D',1,'S',12,'MALags',1,'SMALags',1);
[estimates,~,logL] = estimate(model,ts_data);

% 对模型进行诊断检验
。。。略请下载完整代码

% 输出预测结果
。。。略请下载完整代码