1 Prim算法
1.1 概述
1.1.1 算法描述
算法描述:
-
初始化最小生成树,只有一个起点;
-
每次将下一条连接树中顶点和其补集中顶点且权重最小的边(黑色表示)加入树中;
-
重复步骤中2,直至最小生成树中加入了V-1条边。
命题L。Prim算法能够得到任意加权连通图的最小生成树。
证明:有命题K可知,这颗不断生长的树定义了一个切分切不存在黑色的横切边。该算法会选取权重最小的横切边并根据贪心算法不断将它们标记为黑色。
- 命题K在上一篇文章==0301概述-最小生成树-图-数据结构和算法(Java)==
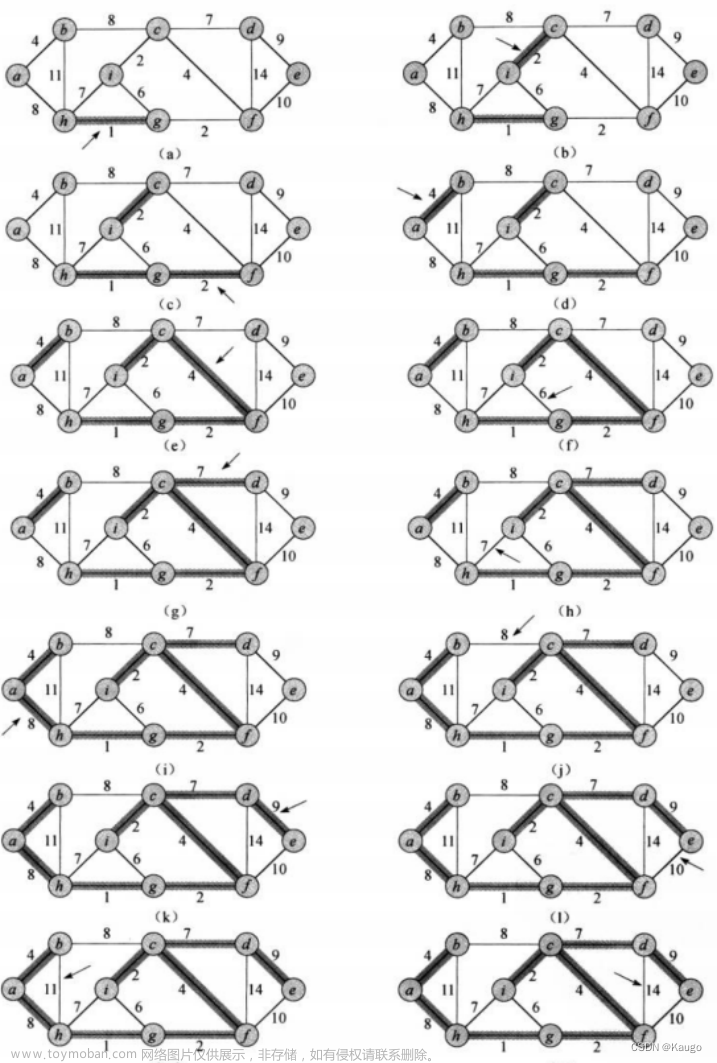
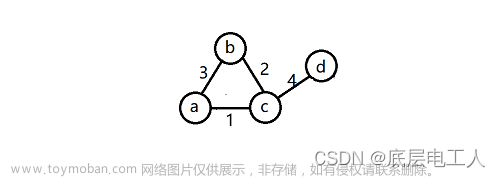
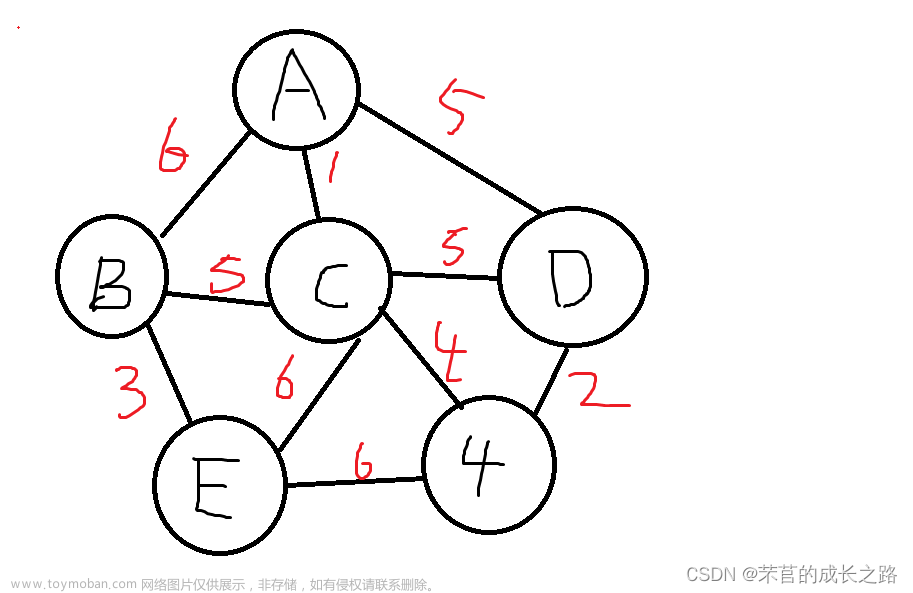
最小生成树Prim算法如下图1.1.1-1所示:

1.1.2 数据结构
实现Prim算法需要用到一些常见的数据结构,我们会用以下方法表示树中的顶点、边和横切边。
- 顶点:使用一个由顶点索引的布尔数组marked[],如果顶点v在树中,那么marked[v]的值为true;
- 边;一条队列mst来保持最小生成树中的边;
- 横切边:使用一条优先队列M in PQ<Edge>来根据权重比较所有边。
- 优先队列可参考之前的文章==堆(二叉堆)-优先队列-数据结构和算法(Java)==和\02优先队列和索引优先队列-优先队列-数据结构和算法(Java)==
有了这些数据结构,我们可以回答“那条边的权重最小?”这个基本问题。
1.1.3 横切边集合维护
- 每当我们向树中添加一条边之后,也向边中添加一个顶点;
- 要维护包含所有横切边的集合,需要将连接这个顶点和其他所有不在树中的顶点边加入优先队列;
- 用marked[]数组来识别这样的边;
- 连接新加入树中顶点和其他已经在树中顶点 的所有边都失效了;
- 这样的边已经不是横切边,因为它的两个顶点都在树中。
- 将失效边从优先队列删除实现
- 延时实现:将这些边先留在优先队列中,等到要删除它们的时候在检查边的有效性;
- 即时实现:将这样的边从优先队列删除。
1.2 延时实现
1.2.1 实现代码
延时实现源代码1.2-1如下所示:
package edu.princeton.cs.algs4;
/**
* 最小生成树Prim算法延时实现
*/
public class LazyPrimMST {
private static final double FLOATING_POINT_EPSILON = 1E-12;
/**
* 最小生成树的总权重
*/
private double weight;
/**
* 最小生成树中边的集合
*/
private Queue<Edge> mst;
/**
* 图中顶点算法在树中标记
*/
private boolean[] marked;
/**
* 维护横切边的优先队列
*/
private MinPQ<Edge> pq;
/**
* 计算最小生成树
* @param G 加权连通图
*/
public LazyPrimMST(EdgeWeightedGraph G) {
mst = new Queue<Edge>();
pq = new MinPQ<Edge>();
marked = new boolean[G.V()];
// 遍历图中所有顶点
for (int v = 0; v < G.V(); v++)
if (!marked[v]) prim(G, v);
// check optimality conditions
assert check(G);
}
/**
* 最小生成树Prim延时算法
*/
private void prim(EdgeWeightedGraph G, int s) {
scan(G, s);
while (!pq.isEmpty()) {
// 获取权重最小的边
Edge e = pq.delMin();
int v = e.either(), w = e.other(v);
assert marked[v] || marked[w];
// 如果边的两个顶点都在树中,跳过
if (marked[v] && marked[w]) continue;
// 该切分中权重最小横切边加入树中
mst.enqueue(e);
weight += e.weight();
if (!marked[v]) scan(G, v);
if (!marked[w]) scan(G, w);
}
}
/**
* 当前切分横切边加入优先队列
*/
private void scan(EdgeWeightedGraph G, int v) {
assert !marked[v];
marked[v] = true;
for (Edge e : G.adj(v))
if (!marked[e.other(v)]) pq.insert(e);
}
/**
* 最小生成树中所有边
*/
public Iterable<Edge> edges() {
return mst;
}
/**
* 最小生成树权重之和
*/
public double weight() {
return weight;
}
/**
* 校验加权连通图
*/
private boolean check(EdgeWeightedGraph G) {
// 校验权重
double totalWeight = 0.0;
for (Edge e : edges()) {
totalWeight += e.weight();
}
if (Math.abs(totalWeight - weight()) > FLOATING_POINT_EPSILON) {
System.err.printf("Weight of edges does not equal weight(): %f vs. %f\n", totalWeight, weight());
return false;
}
// 校验是否有环
UF uf = new UF(G.V());
for (Edge e : edges()) {
int v = e.either(), w = e.other(v);
if (uf.find(v) == uf.find(w)) {
System.err.println("Not a forest");
return false;
}
uf.union(v, w);
}
// 校验是否是生成树森林
for (Edge e : G.edges()) {
int v = e.either(), w = e.other(v);
if (uf.find(v) != uf.find(w)) {
System.err.println("Not a spanning forest");
return false;
}
}
// check that it is a minimal spanning forest (cut optimality conditions)
for (Edge e : edges()) {
// all edges in MST except e
uf = new UF(G.V());
for (Edge f : mst) {
int x = f.either(), y = f.other(x);
if (f != e) uf.union(x, y);
}
// check that e is min weight edge in crossing cut
for (Edge f : G.edges()) {
int x = f.either(), y = f.other(x);
if (uf.find(x) != uf.find(y)) {
if (f.weight() < e.weight()) {
System.err.println("Edge " + f + " violates cut optimality conditions");
return false;
}
}
}
}
return true;
}
}
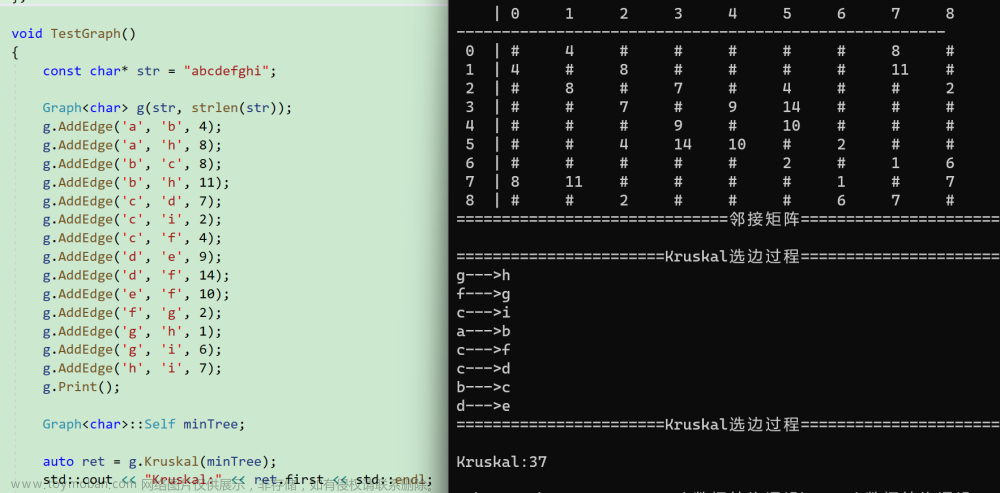
测试代码1.2.1-1如下所示:
public static void testLazyPrim() {
String path = System.getProperty("user.dir") + File.separator + "asserts/tinyEWG.txt";
In in = new In(path);
EdgeWeightedGraph G = new EdgeWeightedGraph(in);
LazyPrimMST mst = new LazyPrimMST(G);
for (Edge e : mst.edges()) {
StdOut.println(e);
}
StdOut.printf("%.5f\n", mst.weight());
}
测试结果:
0-7 0.16000
1-7 0.19000
0-2 0.26000
2-3 0.17000
5-7 0.28000
4-5 0.35000
6-2 0.40000
1.81000
测试用例Prim算法的轨迹图如下1.2.1所示:

1.2.2 性能分析
命题M。Prim算法的延时实现技术一幅含有V个顶点和E条边的加权连通图的最小生成树所需的空间与E成正比,所需的时间和 E log E E\log E ElogE成正比(最快情况)。
证明:算法的瓶颈在与优先队列的insert()和delMin()方法中比较边的权重的次数。优先队列最多可能有E条边,这就是空间需求的上限。在最坏情况下,一次插入的成本为 ∽ lg E \backsim \lg E ∽lgE,删除最小元素 的成本 ∽ 2 lg E \backsim 2\lg E ∽2lgE。因为最多只能插入E条边,删除E次最小元素,时间上限和 E log E E\log E ElogE成正比。
1.3 即时实现
1.3.1 分析
- 优化思想
要改进LazyPrimMST,可以从优先队列中删除失效边入手。
-
我们关心的是连接树顶点和非树顶点中权重最小的边。
-
当我们将顶点v加入到生成树中时,对于每个非树顶点w产生的变化是w到最小生成树的距离更近了。即我们不需要在优先队列中保存所有从w到树顶点的边,而只需要保存其中权重最小的边。
-
我们通过遍历顶点v的连接表,可以实现。这样我们之后在优先队列中保存每个非树顶点w的一条边:当前将w与树中顶点连接起来的权重最小的那条边。
-
结构更换:
- 索引优先队列更换优先队列,因为我们需要访问优先队列中的元素。
- 新增2个索引数组edgeTo[]和disTo[]
- 如果顶点v不在树中但至少含有一条边和树相连,那么edgeTo[v]是将v和树连接的最短边(当前权重最小边),distTo[v]为这条边的权重。
- 所有这类顶点v都保存在一条索引优先队列中,索引关联值是edgeTo[v]的边权重。
1.3.2 实现代码
Prim即使实现算法类PrimMST源代码如下:
package edu.princeton.cs.algs4;
/**
* 最小生成树算法prim即时实现
*/
public class PrimMST {
private static final double FLOATING_POINT_EPSILON = 1E-12;
/**
* 顶点和树连接的最短边
*/
private Edge[] edgeTo;
/**
* 最短边对应的权重
*/
private double[] distTo;
/**
* 顶点是否在树中
*/
private boolean[] marked;
/**
* 维护横切边集合
*/
private IndexMinPQ<Double> pq;
/**
* Compute a minimum spanning tree (or forest) of an edge-weighted graph.
* @param G the edge-weighted graph
*/
public PrimMST(EdgeWeightedGraph G) {
edgeTo = new Edge[G.V()];
distTo = new double[G.V()];
marked = new boolean[G.V()];
pq = new IndexMinPQ<Double>(G.V());
for (int v = 0; v < G.V(); v++)
distTo[v] = Double.POSITIVE_INFINITY;
for (int v = 0; v < G.V(); v++) // run from each vertex to find
if (!marked[v]) prim(G, v); // minimum spanning forest
// check optimality conditions
assert check(G);
}
/**
* prim算法即时实现
*/
private void prim(EdgeWeightedGraph G, int s) {
distTo[s] = 0.0;
pq.insert(s, distTo[s]);
while (!pq.isEmpty()) {
int v = pq.delMin();
scan(G, v);
}
}
/**
* 扫描顶点v的连接表,使优先队列中只保留非树顶点连接树顶点最小边
*/
private void scan(EdgeWeightedGraph G, int v) {
marked[v] = true;
for (Edge e : G.adj(v)) {
int w = e.other(v);
if (marked[w]) continue; // v-w is obsolete edge
if (e.weight() < distTo[w]) {
distTo[w] = e.weight();
edgeTo[w] = e;
if (pq.contains(w)) pq.decreaseKey(w, distTo[w]);
else pq.insert(w, distTo[w]);
}
}
}
/**
* 最小生成树中边
*/
public Iterable<Edge> edges() {
Queue<Edge> mst = new Queue<Edge>();
for (int v = 0; v < edgeTo.length; v++) {
Edge e = edgeTo[v];
if (e != null) {
mst.enqueue(e);
}
}
return mst;
}
/**
* 生成树权重
*/
public double weight() {
double weight = 0.0;
for (Edge e : edges())
weight += e.weight();
return weight;
}
// check optimality conditions (takes time proportional to E V lg* V)
private boolean check(EdgeWeightedGraph G) {
// check weight
double totalWeight = 0.0;
for (Edge e : edges()) {
totalWeight += e.weight();
}
if (Math.abs(totalWeight - weight()) > FLOATING_POINT_EPSILON) {
System.err.printf("Weight of edges does not equal weight(): %f vs. %f\n", totalWeight, weight());
return false;
}
// check that it is acyclic
UF uf = new UF(G.V());
for (Edge e : edges()) {
int v = e.either(), w = e.other(v);
if (uf.find(v) == uf.find(w)) {
System.err.println("Not a forest");
return false;
}
uf.union(v, w);
}
// check that it is a spanning forest
for (Edge e : G.edges()) {
int v = e.either(), w = e.other(v);
if (uf.find(v) != uf.find(w)) {
System.err.println("Not a spanning forest");
return false;
}
}
// check that it is a minimal spanning forest (cut optimality conditions)
for (Edge e : edges()) {
// all edges in MST except e
uf = new UF(G.V());
for (Edge f : edges()) {
int x = f.either(), y = f.other(x);
if (f != e) uf.union(x, y);
}
// check that e is min weight edge in crossing cut
for (Edge f : G.edges()) {
int x = f.either(), y = f.other(x);
if (uf.find(x) != uf.find(y)) {
if (f.weight() < e.weight()) {
System.err.println("Edge " + f + " violates cut optimality conditions");
return false;
}
}
}
}
return true;
}
}
主要算法:
-
将顶点v加入树中后,遍历v的邻接表(边)
-
邻接边对应另外一个顶点w,如果已经在树中,跳过;
-
没在树中,判断非树顶点w与树中顶点v连接边权重是否小于之前记录非树顶点w与树中顶点连接边的权重
- 是,判断索引优先队列算法包含索引w
- 是更新,明确权重比原先的小只需要更新索引对应的权重值后上浮即可;
- 不是新加入
- 是,判断索引优先队列算法包含索引w
测试代码如下1.3.2-2所示:
public static void testPrim() {
String path = System.getProperty("user.dir") + File.separator + "asserts/tinyEWG.txt";
In in = new In(path);
EdgeWeightedGraph G = new EdgeWeightedGraph(in);
PrimMST mst = new PrimMST(G);
for (Edge e : mst.edges()) {
StdOut.println(e);
}
StdOut.printf("%.5f\n", mst.weight());
}
测试结果:
1-7 0.19000
0-2 0.26000
2-3 0.17000
4-5 0.35000
5-7 0.28000
6-2 0.40000
0-7 0.16000
1.81000
1.3.3 性能分析
命题N。Prim算法的即时实现即时一幅含有V个顶点和E条边的连通加权无向图的最小生成树所需的空间和V成正比,所需时间和 E log V E\log V ElogV成正比(最坏情况)。
证明:因为优先队列中的顶点时最多为V,且使用3条由递给你的所有的数组,所以所需空间上限和V成正比。算法会进行V次插入操作,V次删除最小元素操作和(在最坏情况下)E次改变优先级操作。已知在基于堆实现索引优先队列中所有这些操作的增长量级为 log V \log V logV,所以将所有这些加起来可知算法所需时间和 E log V E\log V ElogV成正比。
结语
如果小伙伴什么问题或者指教,欢迎交流。
❓QQ:806797785
⭐️源代码仓库地址:https://gitee.com/gaogzhen/algorithm
参考链接:文章来源:https://www.toymoban.com/news/detail-415294.html
[1][美]Robert Sedgewich,[美]Kevin Wayne著;谢路云译.算法:第4版[M].北京:人民邮电出版社,2012.10.p398-404.文章来源地址https://www.toymoban.com/news/detail-415294.html
到了这里,关于0302Prim算法-最小生成树-图-数据结构和算法(Java)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!