✅作者简介:嵌入式入坑者,与大家一起加油,希望文章能够帮助各位!!!!
📃个人主页:@rivencode的个人主页
🔥系列专栏:玩转数据结构
💬保持学习、保持热爱、认真分享、一起进步!!
一.算法设计的要求
-
正确性
1.程序没有语法错误
2.程序对于一切合法的输入数据包括那些典型、苛刻且带有刁难性的几组输入数据可以得出满足要求的结果(设计算法时需要考虑到所有可能会输入数据) -
可读性
算法写出来是为了人阅读、理解、交流,而不是给计算机看所以我们要有一个良好的代码风格。 -
健壮性
1.当我们输入非法数据时,算法需要进行相应的处理,而不是输出莫名其妙的输出结果。
2.处理出错的方式,不应该是中断程序的执行,而是应返回一个表示错误的值,例如对指针的断言保证数据输入的有效性。 -
高效性
更少的算法执行的时间和算法执行的过程中需要的最大存储空间
二.时间复杂度与空间复杂度
一个好的算法首先要具备正确性,然后是健壮性,可读性,如果上面几方面都满足的情况下,则算法的优劣程度通过算法的效率的高低来决定
算法效率:
1.时间效率:指的是算法执行过程耗费的时间
2.空间效率:指的是算法执行过程所耗费的最大的存储空间
有时候时间效率与空间效率是相互矛盾的,要时间则要牺牲空间,要空间则要牺牲时间。
算法时间效率的度量:
算法时间效率可以用算法程序在计算机上执所消耗的时间来度量
两种度量方法:
-
事后统计
将算法先实现,直接将算法程序在计算机上运行,测算其时间和空间的开销
这种方式有着极大的缺陷:首先需要编写程序实现算法需要花费较多的时间和精力,如果算法很劣质一切要推倒重来,第二在不同的计算机的软硬件(CPU的好坏)等环境下,测出的结果也大相庭径,所以会掩盖算法本身的优劣。
所以这种方式直接淘汰 -
事前分析
对算法所消耗的资源进行估算,一定要理解这个估算的概念,后面会具体讲如何进行估算。
事前分析法:
一个算法的运行时间是指一个算法在计算机上运行的时间大致可以等于计算机执行一种简单的操作(如赋值、比较、移动、判断、打印等等)所需的时间与算法中进行简单操作的次数的乘积
算法运行时间=一个简单操作所需的时间 * 简单操作的总次数
而这些简单操作,也就是C语言的中一条一条语句:
算法运行时间= 每条语句频度之和 * 该语句执行一次所需的时间
但问题来了每条语句执行的时间,一般取决于计算机(CPU等硬件的好坏)的指令性能、速度、以及编译的代码质量,所以与算法无关,此时我们就可以假设执行每条语句所需的时间均为单位时间,所以算法的运行时间只跟所有语句的执行次数有关啦.
例如:两个n*n矩阵相乘的算法:
但如果这样算是不是未免太麻烦了,要去算出每条语句的执行次数,而且也体现不出我们估算的本质
所以为了便于比较不同算法的时间效率,我们仅仅比较他们的数量级,数量级越高算法执行的时间越长,算法越劣。
重点来了:若有某个辅助函数f(n),使得当n趋近于无穷大时,T(n)/f(n)的极限值为不等于零的常数,则称f(n)是T(n)的同数量级函数。记作T(n)=O(f(n))称O(f(n)) 为算法的渐进时间复杂度(O代表数量级的意思) ,简称时间复杂度
上面就是官方给出的定义是不是有点晦涩难懂,其实它的意思就是要我们找执行次数数量级最高的那个语句
总结:
算法效率分析分为两种:第一种是时间效率,第二种是空间效率
-
时间效率被称为时间复杂度
时间复杂度:算法中的基本语句重复的执行次数,为算法的时间复杂度
什么是基本语句:对算法运行时间的贡献最大,也就是执行次最多的语句 -
空间效率被称作空间复杂度
空间复杂度:空间复杂度算的是变量的个数
算变量的个数而不是具体使用了多少个字节的空间,其实也是一种估算的方法,也使用大O渐进表示法
注意:经过计算机行业的迅速发展,计算机的存储容量已经达到了很高的程度。所以我们如今已经不需要再特别关注一个算法的空间复杂度,也就是说大多数时候都是用空间换取时间,但是某些存储容量比较小的微控制器例如单片机还是需要考虑一下空间复杂度。
推导大O阶方法:
1、用常数1取代运行时间中的所有加法常数。
2、在修改后的运行次数函数中,只保留最高阶项。
3、如果最高阶项存在不是1,则去除与这个项目相乘的常数。得到的结果就是大O阶。
接下来重点来了前面为什么要说一个算法的运行时间
大致可以等于计算机执行一种简单的操作所需的时间与算法中进行简单操作的次数的乘积,但为什么是大致想过没有,严格意义上上面算的算法运行时间是不准确的。
因为计算机程序执行是一条一条汇编指令,而C语言的一条语句(赋值、比较、移动、打印)不同的语句最后转化为的汇编指令的数目也不同,真正准确的算法运行时间应该等于所以所有汇编指令的数目 * 一条汇编指令的运行时间。
但既然不同C语言语句的对应的汇编指令的数目相差这么大,那为什么还要以算法运行时间与C语言语句执行次数相关联呢,原因有二:
一:如果我们去找C语言各条语句对应汇编的指令的数目实在非常麻烦,狗都不找。
二:多几条汇编指令少几条汇编指令对我们求解算法的时间复杂度一点影响都没有,因为我们要找的是执行次数最多的语句,而且是数量级来表示,最高数量级的系数会被去掉,其他低数量级也会被去掉,所以我们去纠结多一条指令少几条指令根本就没有意义。
具有两个未知数:
最坏时间复杂度
在有些情况下,算法中的基本语句重复执行的次数还随问题的输入的数据集不同而不同
先看例题:
在一个元素大小为N的字符串中寻找一个字符character(由我们输入)
最坏时间复杂度:任意输入规模的最大运行次数(上界)
平均时间复杂度:任意输入规模的期望运行次数
最好时间复杂度:任意输入规模的最小运行次数(下界)
例如:在一个长度为N数组中搜索一个数据x
最好情况:1次找到
最坏情况:N次找到
平均情况:N/2次找到
在实际中一般情况关注的是算法的最坏运行情况,所以数组中搜索数据时间复杂度为O(N),以保证算法的运行时间不会比它更长
常数阶-O(1)

这里在提醒一下这里千万不要计较语句具体执行的次数,如果要深究起来,计算机执行指令的次数绝对比24次要大的多,因为C语句最后翻译成汇编指令数目一定会增加,但是就跟我们前面所说多几条汇编指令少几条汇编指令对我们求解算法的时间复杂度一点影响都没有。
我们采用大O渐进表示法就是为了估算算法执行的时间
线性阶-O(n)

上面算了每条语句的执行次数这是方便理解这些方法,我们不用算每条语句的执行次数,其实我们可以直接找对算法运行时间的贡献最大,也就是执行次最多的语句的执行次数。

递归求N的阶乘
long long Factorial(size_t N)
{
return N < 2 ? N : Factorial(N-1)*N;
}

平方阶-O(n^2)

如果在多一层循环就是 O(n^3)

对数阶-O(logn)


空间复杂度
空间复杂度:空间复杂度算的是变量的个数
算变量的个数而不是具体使用了多少个字节的空间,其实也是一种估算的方法,也使用大O渐进表示法
将一维数组a中n元素逆序存放到原数组中。

递归求N的阶乘
long long Factorial(size_t N)
{
return N < 2 ? N : Factorial(N-1)*N;
}

练习:
1.消失的数组
数组nums包含从0到n的所有整数,不一定有序,但其中缺了一个。请编写代码找出那个缺失的整数。你有办法在O(n)时间内完成吗?

思路一:
先将数组排序,然后数组前一个元素与后一个元素比较 遍历数组,若后一个元素的值减去前一个元素的值不为1则该元素的下标的值就是缺失的整数。
但是此种方法排序的最低的时间复杂度都要 最快排序O(nlogn)>题目要求的O(n)
思路二:
将0到N的值加到一起减去数组的元素值的加到一起,结果就是缺失的整数,时间复杂度是符合要求的,但是太简单了不讲。
思路三:
用异或的思想,在此之前我们先来了解异或的特点。
运算法则:
同值取0,异值取1;
1^1=0
0^0=0
1^0=1
0^1=1
性质:
1.交换律 a^ b = b^a
2.结合律 a^ b ^ c = a^ (b^c)
3.对于任何数x x^x=0, x ^ 0=x
不用临时变量交换两个数:
消失的数组实现思路:
数组的数依次与0~N的所有数进行异或,把相同的数字都消除(等于0),最后剩下的数据就是缺失的整数。
其中就利用了异或的交换律,把相同的数字放在一起异或等于0,剩下的数据就是缺失的整数。
//消失的数组
int Miss_Number(int * nums,int size)
{
int x=0;
int i=0;
int j=0;
//先跟数组的值异或
for(i=0;i<size;i++)
{
x^=nums[i];
}
//再与0~n之间的数异或
for(j=0;j<size+1;j++)
{
x^=j;
}
return x;
}
int main()
{
int nums[]={9,6,4,2,3,5,7,0,1};
int size=sizeof(nums)/sizeof(nums[0]);
printf("missnum=%d\n",Miss_Number(nums,size));
return 0;
}
实验结果:
2.旋转数组
给你一个数组,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。
进阶:
尽可能想出更多的解决方案,至少有 三种 不同的方法可以解决这个问题。你可以使用空间复杂度为 O(1) 的 原地 算法解决这个问题吗?
思路一:
进阶:
先把数组nums最后一个元素放到一个临时变量tmp,然后从倒数第二个元素依次往后移动,再把 tmp 存的最后一个元素的值赋给数组nums[0],相当旋转一次,然后循环K次的话,相当于就旋转了K次。
该时间复杂度为O(N*K),效率较低
void Rotate(int * nums,int size, int k)
{
while(k--)
{
for(int i=0; i<k; i++)
{
//先把数组nums最后一个元素放到一个临时变量tmp
int tmp=nums[size-1];
for(int end =size-2; end>=0; end--)
{
nums[end+1]=nums[end];
}
//再把 tmp 存的最后一个元素的值赋给数组nums[0]
nums[0] =tmp;
}
}
}
思路二:以空间换时间
创建一个大小与nums数组相同的数组,将nums最后面要旋转的K个元素放到新数组的前k个元素空间内,其他元素放在新数组的k个元素之后,此时要遍历数组算法的时间复杂度为O(n),开辟的n个元素的数组,空间复杂度为O(n),不符合题目要求空间复杂度为O(1)。
思路三:
后k个逆置
前n-k个逆置
再整体逆置
代码实现:
void Reverse(int *arr,int left, int right)
{
int tmp=0;
while(left<right)
{
tmp=arr[left];
arr[left]=arr[right];
arr[right]=tmp;
right--;
left++;
}
}
void Rotate_num(int* arr,int n,int k)
{
if (k>n)
{
k=k%n;
}
//后k个逆置
Reverse(arr,n-k,n-1);
//前n-k个逆置
Reverse(arr,0,n-k-1);
//再整体逆置
Reverse(arr,0,n-1);
}
int main()
{
int i;
int arr[7]={1,2,3,4,5,6,7};
Rotate_num(arr,7,3);
for(i=0;i<7;i++)
{
printf("%d ",arr[i]);
}
return 0;
}

注意:若旋转次数k=n数组元素个数,相当于又把数组旋转回来了,相当于数组没变,如果k>n 例如 n=7 k=8,那就相当于只旋转了一次(8%7=1)文章来源:https://www.toymoban.com/news/detail-415646.html
总结


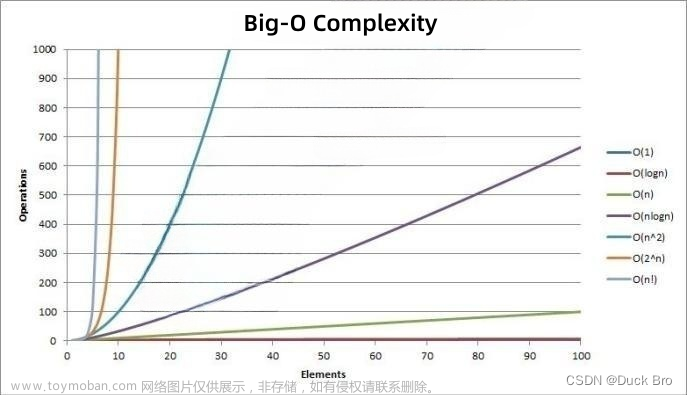
从图上可知,数量级越高,计算机执行执行次数的增长率越快。文章来源地址https://www.toymoban.com/news/detail-415646.html
到了这里,关于深入理解时间和空间复杂度的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!