梯度下降
梯度下降(Gradient Descent)是一种常用的优化算法,用于求解目标函数的最小值。(在机器学习应用梯度下降中,主要目标是为了最小化损失函数);
其基本思想是通过不断迭代调整参数,使得目标函数的值不断逼近最小值。(机器学习中是为了最小化损失函数,即使得预测值与实际值之间的差值最小);
在每一次迭代中,算法会计算当前参数的梯度值,然后将参数朝着梯度下降的方向进行更新,从而达到逐步降低目标函数值的目的。
总而言之,梯度下降之于机器学习:
-
目标和意义:
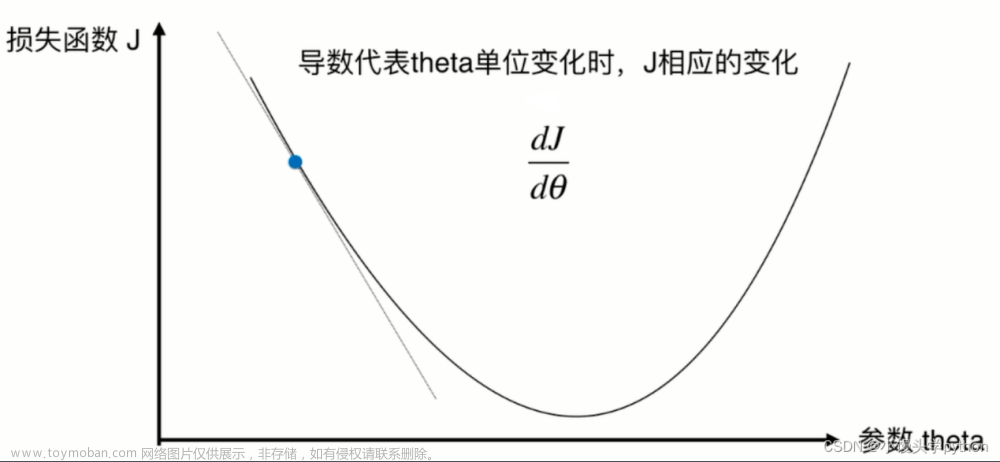
梯度下降算法的目标是最小化损失函数,通过计算损失函数对权重的偏导数(即梯度)来确定更新权重的方向和大小。 -
基本公式:
θ i + 1 = θ i − α ∂ J ( θ ) ∂ θ \theta_{i+1} = \theta _i - \alpha \frac {\partial J(\theta)} {\partial \theta} θi+1=θi−α∂θ∂J(θ) -
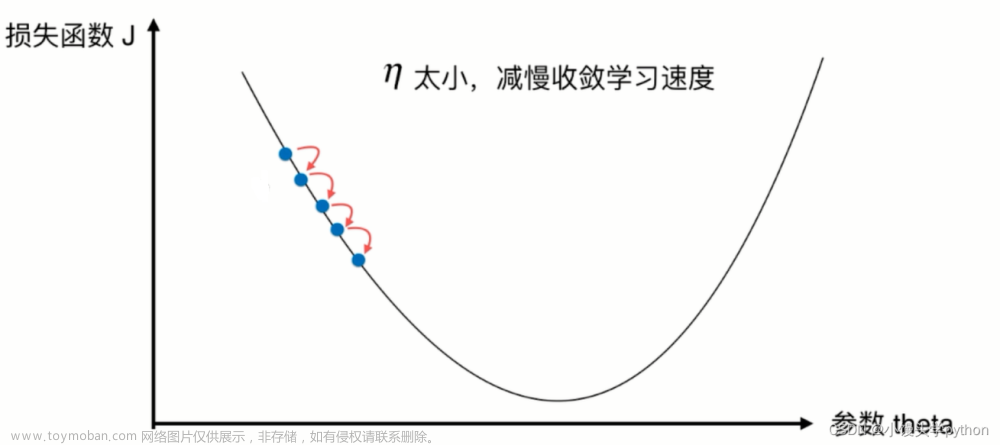
学习率:
学习率决定了每次迭代中,参数更新的幅度,如果学习率设置得过大,可能会导致参数不断在损失函数的最小值两侧来回震荡,无法收敛;而如果学习率设置得过小,可能会导致参数更新速度过慢,收敛速度变慢。
因此,合适的学习率对梯度下降算法的收敛速度和效果至关重要。
梯度下降算法
梯度下降算法,我分为两个派系共计7个算法:
-
基础优化算法:
批量梯度下降 BGD随机梯度下降 SGD小批量梯度下降 MBGD动量梯度下降 MGD -
基础优化算法上改进和优化的算法:
自适应梯度算法 Adagrad均方根传播算法 RMSProp自适应矩估计算法 Adam
省流来说,无脑用 Adam 就行;剩余分析内容如下
基础优化算法
批量梯度下降 BGD
批量梯度下降算法 Batch Gradient Descent,在每次迭代时使用全部的训练数据来计算梯度,然后用这个梯度更新模型参数。因此,BGD 的运行时间与训练数据的大小成正比,当数据集很大时,它的运行时间会很长。
具体来说,BGD 的流程如下:
- 初始化模型参数,例如随机赋值。
- 计算训练数据集的损失函数。
- 计算损失函数的梯度,即对所有样本的梯度进行求和并求平均值,注意是所有训练样本。
- 使用梯度下降的公式来更新模型参数,使得损失函数减小。
- 重复 2~4 步,直到损失函数达到满意的值或达到最大迭代次数。
批量梯度下降 Batch Gradient Descent 的优点是可以全局优化模型,有效的避免局部最优解的出现,但是无法完全规避局部最优解;但相比于其他优化算法,它的局部最优解问题较少。同时,BGD 收敛速度相对较快。
缺点是需要遍历整个训练集,计算梯度的时间较长,不适合大规模数据集的训练。另外,BGD 对于数据集中存在噪声或异常值的情况比较敏感,需要进行数据预处理或采用其他优化算法。
随机梯度下降 SGD
随机梯度下降算法 Stochastic Gradient Descent 与批量梯度下降算法不同的是,它不是计算所有样本的梯度来更新模型参数,而是从训练集中随机选择一个样本计算梯度,并使用该样本梯度来更新参数。
带着疑惑,SGD 的流程如下:
- 初始化模型参数,通常为随机值。
- 随机从训练集中选择一个样本。
- 计算该样本的损失函数在当前模型参数处的梯度。
- 使用计算出的梯度来更新模型参数。
- 重复步骤2-4,直到达到预设的停止条件。
很明显,SGD每次只需要计算一个样本的梯度,所以计算速度快,适合大规模数据集。
更明显,由于随机性的存在,可能导致每次更新参数的方向不一样,可能会导致算法在训练过程中出现震荡现象,需要增加一些技巧来解决这个问题。
在SGD的基础上,还有一些改进的算法,如批量随机梯度下降(Mini-Batch SGD)和动量梯度下降(Momentum),它们可以更好地平衡计算速度和算法稳定性,使得训练过程更加高效和可靠。
小批量梯度下降 MBGD
小批量梯度下降算法,Mini-Batch Gradient Descent,在每次迭代时仅使用部分数据(即一个小批量)来计算梯度,从而减少计算量,加快收敛速度,同时也能提高收敛的稳定性。
带着灵光乍现,MBGD 的流程如下:
- 随机选择一个大小为 m 的小批量数据,其中 m 通常是 2 的整数次幂,可以根据实际情况进行调整。
- 计算这个小批量数据的平均梯度。
- 根据计算出的平均梯度更新模型参数,即执行参数更新公式:θ = θ - α * g,其中θ表示模型参数,α表示学习率,g表示平均梯度。
- 重复步骤1-3,直到达到收敛条件或达到预设的迭代次数。
很明显,MBGD 是 BGD 与 SGD 的一种折中算法,包含两个的优势。算的快,收敛的快,更稳定;
动量梯度下降 MGD
动量梯度下降,Momentum Gradient Descent,在更新参数时,除了考虑当前的梯度,还要考虑之前梯度的方向和大小。具体来说,MGD引入了一个动量变量,用来记录之前的梯度方向,然后将当前梯度方向和动量方向结合起来进行参数更新。
带着些许点头,MGD 的流程如下:
- 初始化动量变量v为0。
- 计算当前的梯度g。
- 更新动量变量v:v = βv + (1-β)g,其中β是一个介于0和1之间的动量系数。
- 根据动量变量v和当前梯度g的和来更新模型参数:θ = θ - α(v+g),其中α是学习率。
- 重复执行2-4步,直到达到收敛条件或达到预设的迭代次数。
感觉上,好像动量梯度下降在小批量梯度下降上做了一些优化,即加上了一个参数——动量变量,但是真的有很好的优化效果吗?
但是事实上不一定,并不是说只要选择合适的动量变量v,MGD 就一定优于 MBGD;
优化算法的选择,需要考虑很多因素的影响,比如数据集大小、模型复杂度、超参数设置等等。对于不同的问题,可能需要不同的优化算法才能获得最好的效果。
同时,MGD 中选择动量变量 v 的大小也是需要进行调整的,如果设置得不合适,也可能导致收敛速度变慢或不稳定的收敛。
基础优化算法上的改进和优化的算法
自适应梯度算法 Adagrad
Adagrad在每个参数处维护一个二次累积梯度的平方和,用于根据参数的历史梯度信息自适应地调整学习率。每次迭代时,Adagrad根据当前参数的梯度计算其二次累积梯度的平方和,并使用该平方和来更新参数的学习率。
带着什么是“二次累积梯度”的疑问,Adagrad 更新参数的公式如下:
θ
t
+
1
,
i
=
θ
t
,
i
−
α
G
t
,
i
i
+
ϵ
g
t
,
i
\theta_{t+1, i} = \theta_{t,i} - \frac {\alpha} {\sqrt{G_{t,ii} + \epsilon}}g_{t,i}
θt+1,i=θt,i−Gt,ii+ϵαgt,i
其中
θ
t
+
1
,
i
\theta_{t+1, i}
θt+1,i 为第
i
i
i 个参数在
t
+
1
t+1
t+1 时刻,即更新后的取值;
对应的
θ
t
,
i
\theta_{t, i}
θt,i 即为第
i
i
i 个参数在
t
t
t 时刻,即更新前的取值;
α
\alpha
α 学习率;
g
t
,
i
g_{t,i}
gt,i 该参数在
t
t
t 时刻的梯度;
G
t
,
i
i
G_{t,ii}
Gt,ii 是参数在
t
t
t 时刻的二次累积梯度平方和;
ϵ
\epsilon
ϵ 是一个非常小的常数,用于规避分母为 0 的情况;
- 什么是二次累积梯度平方和?
二次累积梯度平方和,也称为 历史梯度平方和,用来自适应地调整参数的学习率。具体地,假设在前 t t t 个时刻中,第 i i i 个参数 θ i \theta_i θi 的梯度为 g 1 , i , g 2 , i , … , g t , i g_{1,i}, g_{2,i}, \dots, g_{t,i} g1,i,g2,i,…,gt,i,那么它在第 t t t 个时刻的二次累积梯度平方和为:
G t , i i = ∑ k = 1 t ( g k , i ) 2 G_{t,ii} = \sum _{k=1} ^{t} (g_{k,i})^2 Gt,ii=k=1∑t(gk,i)2
具体来说,Adagrad算法中,二次累积梯度平方和 G t , i i G_{t,ii} Gt,ii 可以被看做是每个参数 θ i \theta_i θi 的历史梯度信息的加权平均,其中较大的梯度会获得较小的权重,较小的梯度会获得较大的权重,从而达到自适应调整学习率的目的。
根据 Adagrad 更新参数的公式:
θ
t
+
1
,
i
=
θ
t
,
i
−
α
G
t
,
i
i
+
ϵ
g
t
,
i
\theta_{t+1, i} = \theta_{t,i} - \frac {\alpha} {\sqrt{G_{t,ii} + \epsilon}}g_{t,i}
θt+1,i=θt,i−Gt,ii+ϵαgt,i
我们发现 二次累计梯度平方和 出现在:
α
G
t
,
i
i
+
ϵ
\frac {\alpha} {\sqrt{G_{t,ii} + \epsilon}}
Gt,ii+ϵα
其中, ϵ \epsilon ϵ 是一个非常小的常数,意义就是为了防止分母部分为0,而如果某个参数 θ i \theta_i θi 在之前的迭代中 梯度 g t , i g_{t,i} gt,i 比较大,那么对应的 二次累积梯度平方和 G_{t,ii} 就比较大,因此在后续的迭代中,该参数的学习率部分 α G t , i i + ϵ \frac {\alpha} {\sqrt{G_{t,ii} + \epsilon}} Gt,ii+ϵα 会减小,使得它在参数空间中移动的步长变小,从而更加稳定地接近最优点。反之,如果某个参数在之前的迭代中梯度比较小,那么对应的二次累积梯度平方和就比较小,因此在后续的迭代中,该参数的学习率会增大,使得它在参数空间中移动的步长变大,从而更快地接近最优点。
因此,Adagrad算法使用二次累积梯度平方和来调整每个参数的学习率,能够自适应地为不同的参数分配不同的学习率,从而更加有效地优化模型。
均方根传播算法 RMSProp
与Adagrad算法类似,RMSProp算法也使用了梯度的二次累积信息,但是与Adagrad算法不同的是,RMSProp算法对梯度的二次累积信息进行了指数加权移动平均(Exponential Moving Average,EMA),而不是简单的累加和。
具体来说,对于某个参数
w
w
w 的梯度
g
t
g_t
gt,RMSProp算法使用如下的指数加权移动平均公式计算它的二次累积梯度平方和:
v
t
=
β
v
t
−
1
+
(
1
−
β
)
g
t
2
v_t = \beta v_{t-1} + (1-\beta) g_t^2
vt=βvt−1+(1−β)gt2
其中, v t v_t vt 表示第 t t t 是迭代时参数 w w w 的二次累积梯度平方和, β \beta β 是一个介于0~1 之间的衰减率,用来控制历史梯度信息的权重大小,通常取值 0.9 或 0.99;
剩下的部分同 Adagrad,即 RMSProp 的更新参数的公式为:
θ
t
+
1
,
i
=
θ
t
,
i
−
α
v
t
+
ϵ
g
t
,
i
\theta_{t+1, i} = \theta_{t,i} - \frac {\alpha} {\sqrt{v_t + \epsilon}}g_{t,i}
θt+1,i=θt,i−vt+ϵαgt,i
RMSProp算法根据每个参数的历史梯度信息来自适应地调整学习率,如果某个参数的梯度比较大,那么它的二次累积梯度平方和也会比较大,此时它的学习率会减小,使得它在参数空间中移动的步长变小,从而更加稳定地接近最优点。
反之,如果某个参数的梯度比较小,那么它的二次累积梯度平方和也会比较小,此时它的学习率会增大,使得它在参数空间中移动的步长变大,从而更快地接近最优点。
总的来说,RMSProp算法相比于传统的梯度下降算法,能够自适应地调整每个参数的学习率,从而更加高效地优化模型。
对比 Adagrad 与 RMSProp 来看,
RMSProp只考虑最近一段时间的历史梯度平方和,而不是所有历史的平方和(Adagrad),所以它可以更快地适应梯度的变化,并且可以处理非凸优化问题中的局部极小值。
可以认为RMSProp可以缓解Adagrad中因为一开始参数非常大而后来比较小,但是值一直比较大所以 α \alpha α 一直很大,导致下降快的问题。
在实际应用中,我们需要根据具体情况选择适合的梯度优化算法。例如,在处理稀疏数据时,Adagrad可能更适合;而在处理非凸优化问题时,RMSProp可能更适合。
自适应矩估计算法 Adam
Adam是非常常用的自适应优化算法,可以自适应地调整每个参数的学习率,并具有一些正则化的特性。是 Adagrad 和 RMSProp 的扩展版本,同时具备 Adagrad 和 RMSProp 的优点,同时引入了动量的概念。
具体来说,Adam算法通过以下步骤进行参数更新:
- 计算梯度的一阶矩估计(均值)和二阶矩估计(方差),分别表示为 m m m 和 v v v,它们分别初始化为 0。
- 计算梯度 g t g_t gt;
- 计算当前梯度的一阶矩估计
m
m
m 和二阶矩估计
v
v
v 的加权平均值,分别表示为 m_hat 和 v_hat。具体来说,对于每个参数
θ
i
θ_i
θi,它们的更新方式为:
m = β 1 ∗ m + ( 1 − β 1 ) ∗ g t v = β 2 ∗ v + ( 1 − β 2 ) ∗ g t 2 m = \beta_1 * m + (1-\beta_1) * g_t \\ v = \beta_2 * v + (1-\beta_2) * g_t ^2 m=β1∗m+(1−β1)∗gtv=β2∗v+(1−β2)∗gt2
超参数 β 1 \beta_1 β1 与 β 2 \beta_2 β2
在Adam算法中,超参数β1和β2分别控制一阶矩和二阶矩的指数衰减率,它们的作用是平衡历史梯度信息和当前梯度信息对参数更新的影响。
具体来说,β1控制历史梯度信息的衰减速度,它通常取0.9。这意味着当前的梯度在计算一阶矩估计时所占的权重为0.1,历史梯度在计算一阶矩估计时所占的权重为0.9,因此一阶矩估计可以平滑历史梯度信息,使得参数更新更加稳定。
β2控制二阶矩估计的衰减速度,它通常取0.999。这意味着当前的梯度平方在计算二阶矩估计时所占的权重为0.001,历史梯度平方在计算二阶矩估计时所占的权重为0.999,因此二阶矩估计可以平滑历史梯度平方信息,使得参数更新更加稳定。
调整β1和β2的值可以对Adam算法的性能产生重要影响。通常情况下,β1和β2的值是不需要进行调整的,因为它们已经在大量实验中被证明是比较合适的取值。但是,在一些特殊的任务中,可能需要根据具体情况来调整β1和β2的值,以达到更好的优化效果。
接上述公式步骤部分:
-
矫正偏差:在Adam算法中,由于一阶矩和二阶矩的初始估计值都是0,因此在算法的初期阶段,这些估计值会受到偏差影响,导致算法表现不佳。为了解决这个问题,Adam算法引入了偏差校正机制。
偏差校正通过在计算一阶矩和二阶矩估计值时,除以一个偏差校正因子来进行校正。这个偏差校正因子是由当前的迭代次数t和指数衰减率β1、β2共同决定的。
通过偏差校正,可以减轻一阶矩和二阶矩估计值受到初始值偏差的影响,从而提高算法的表现。特别是在算法的初期阶段,偏差校正的效果更加显著,可以使算法更快地收敛。
总之,偏差校正是Adam算法中非常重要的一部分,它可以减轻算法受到初始值偏差的影响,提高算法的表现。
m h a t = m / ( 1 − β 1 t ) v h a t = v / ( 1 − β 2 t ) m_{hat} = m / (1-\beta_1^t)\\ v_{hat} = v / (1-\beta_2^t) mhat=m/(1−β1t)vhat=v/(1−β2t) -
更新参数:
θ = θ − α v h a t + ϵ m h a t \theta = \theta - \frac {\alpha} {\sqrt {v_{hat}} + \epsilon}m_{hat} θ=θ−vhat+ϵαmhat
其中, m h a t m_{hat} mhat 为动量估计量,包含 gradient 信息,而 v h a t v_{hat} vhat 则为RMSProp 梯度的指数加权平均值,当梯度变化剧烈时,v 的值会变得较大,导致更新步长较小;而当梯度变化较小时,v 的值会变得较小,导致更新步长较大。这样就能够平衡梯度的变化和更新步长,从而更好地优化模型。
在训练神经网络时,Adam Optimizer通常是一种非常实用的优化算法,因为它能够自适应地调整每个权重的学习率,从而更快地收敛,并且在超参数设置上相对简单。
所以,回头来看,基础优化算法,其实是在梯度下降的训练数据集规模上做选择,是全部训练数据集(BGD),还是就一个训练数据(SGD),还是一部分训练数据(MBGD);而基础优化算法的改进上,都是围绕如何合理动态规划学习率 α \alpha α 来控制下降的快慢。
代码如何实现梯度下降
Tensorflow 举例 Adam Gradient Descent:

Adam 自适应矩估计算法,通过对每个参数的学习率进行控制;在tensorflow中代码实现如下:
import tensorflow as tf
model.compile(optimizer=tf.keras.optimizers.Adam(learning_rate=1e-3))
如何判断收敛
几种常见的判断模型是否收敛的方法:
-
损失函数下降: 在训练过程中,损失函数会逐渐下降,如果损失函数已经下降到一定程度而不再变化,可以判定模型已经收敛。
-
参数变化: 模型的参数在训练过程中会发生变化,如果模型的参数值已经趋于稳定,说明模型已经收敛。
-
梯度变化: 梯度代表了损失函数的变化趋势,如果梯度变化已经趋于平缓,说明模型已经收敛。
-
验证集误差: 在训练过程中,可以使用验证集验证模型的泛化性能,如果验证集误差已经趋于稳定,说明模型已经收敛。文章来源:https://www.toymoban.com/news/detail-415678.html
综上所述,无法收敛不仅仅是准确率不能提高,还有可能是损失函数不下降、参数变化过大、梯度变化过大、验证集误差波动等情况。因此,在实际应用中,需要综合考虑多种指标来判断模型是否收敛。文章来源地址https://www.toymoban.com/news/detail-415678.html
到了这里,关于【机器学习】P17 梯度下降 与 梯度下降优化算法(BGD 等 与 Adam Optimizer、AdaGrad、RMSProp)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!