1.预设场景
小明要去这样的城市旅游（城市交通图如下），为了减轻经济负担，小明想知道任意两个城市之间的最短路径。
从图中，可以得到：小明打算去4个城市（节点数）旅游，而这4个城市之间有8条公路（边数）连通，公路上的数字（权重）表示这条公路的长短。
现在需要设计一种算法求得任意两个城市之间的最短路径，也就是任意两个点之间的最短路径。该问题的求解也被称为“多源最短路径”。
2.数据结构描述
通常，在存储图的信息时，可以采用二维矩阵来表示。
在案例中，有四个城市，可以用一个5*5的二维矩阵e来存储信息（二维矩阵的0行和0列不存储信息）。比如：1号城市到2号城市的距离为2，则e[1][2] = 2；2号城市没有路可以到达4号城市，则e[2][4] = ∞（INT_MAX）。另外，规定一个城市自己到自己的路程也是0，即e[1][1] = 0。
按照上述描述，初始的二维矩阵如下：
3.Floyd_Warshall具体过程
在求得任意两个节点之间的最短距离时，可以认为初始化矩阵（上图）中的距离即为最短，然后通过引入其他城市作为中间节点，更新这个距离。
通过观察可以发现，每个顶点都有可能使得另外两个顶点之间得路程变短（e[4][1]+e[1][3] = 11 < e[4][3] = 12。而且当任意两个节点之间不允许经过第三个点时，这些城市之间得最短路径就是初始路程。
具体过程如下：
- 先将二维矩阵初始化为“2.数据结构描述”中所要求的。
- 只允许经过1号顶点（中间节点为1），求任意两点之间的最短路径：只需判断e[i][1]+e[1][j]是否小于e[i][j]，如果e[i][1]+e[1][j] < e[i][j]，则更新i->j的最短距离。e[i][j]表示i号顶点到j号顶点的距离。e[i][1]+e[1][j]表示i号顶点到1号顶点，再从1号顶点到j号顶点的距离之和。
具体代码实现如下：
for (int i = 1; i <= vertice; i++)
{
for (int j = 1; j <= vertice; j++)
{
if (e[i][1] < INT_MAX && e[1][j]<INT_MAX && e[i][j] > e[i][1] + e[1][j])
{
e[i][j] = e[i][1] + e[1][j];
}
}
}
在只允许经过1号顶点（中间节点为1）的情况下，任意两个顶点之间的最短距离更新为：
- 判断在允许经过1号顶点和2号顶点的情况下，任意两个顶点之间的路径是否会变得更短。因为第1步已经判断过1号顶点为之间节点，所以在本次判断1号节点和2号节点时只需要在步骤1的结果上加入2号节点即可，也就是：只需判断e[i][2]+e[2][j]是否小于e[i][j]，如果e[i][2]+e[2][j] < e[i][j]，则更新i->j的最短距离。e[i][j]表示i号顶点到j号顶点的距离。e[i][2]+e[2][j]表示i号顶点到2号顶点，再从2号顶点到j号顶点的距离之和。
for (int i = 1; i <= vertice; i++)
{
for (int j = 1; j <= vertice; j++)
{
if (e[i][2] < INT_MAX && e[2][j]<INT_MAX && e[i][j] > e[i][2] + e[2][j])
{
e[i][j] = e[i][2] + e[2][j];
}
}
}
在允许经过1号顶点和2号顶点的情况下，任意两个顶点之间的最短距离更新为：
4. 判断在允许经过1号顶点，2号顶点和3号顶点的情况下，任意两个顶点之间的路径是否会变得更短。因为第2步已经判断过1，2号顶点为之间节点，所以在本次判断1号节点，2号节点和3号顶点时只需要在步骤2的结果上加入3号节点即可，也就是：只需判断e[i][3]+e[3][j]是否小于e[i][j]，如果e[i][3]+e[3][j] < e[i][j]，则更新i->j的最短距离。e[i][j]表示i号顶点到j号顶点的距离。e[i][3]+e[3][j]表示i号顶点到3号顶点，再从3号顶点到j号顶点的距离之和。
for (int i = 1; i <= vertice; i++)
{
for (int j = 1; j <= vertice; j++)
{
if (e[i][3] < INT_MAX && e[3][j]<INT_MAX && e[i][j] > e[i][3] + e[3][j])
{
e[i][j] = e[i][3] + e[3][j];
}
}
}
在允许经过1号顶点和2号顶点的情况下，任意两个顶点之间的最短距离更新为：
4. 同理，可以得到在允许所有顶点作为中转，任意两点之间的最短距离为：
3.代码实现
#include <vector>
#include <iostream>
using namespace std;
class Floyd_Warshall
{
private:
int vertice = 0;//顶点数
int edge = 0;//边数
vector<vector<int>> e;
public:
Floyd_Warshall(int x, int y) :vertice(x), edge(y)
{
//图的初始化从下标1开始
e.resize(vertice + 1);//初始化二维数组的行
for (int i = 0; i <= vertice; i++)
{
e[i].resize(vertice + 1);//初始化二维数组的列
}
}
//图的初始化
void Init_Floyd()
{
for (int i = 0;i <= vertice; i++)
{
for (int j = 0; j <= vertice; j++)
{
if (i == 0 || j == 0)
{
e[i][j] = 0;
}
if (i == j)
{
e[i][j] = 0;
}
else
{
e[i][j] = INT_MAX;
}
}
}
}
//读入图的边
void GetEdgeInfo()
{
cout << "输入边的信息（节点1，节点2，权重）：" << endl;
int e1 = 0, e2 = 0, weigth = 0;
for (int i = 1; i <= edge; i++)
{
cin >> e1 >> e2 >> weigth;
e[e1][e2] = weigth;
}
}
//打印
void Print()
{
for (int i = 1; i <= vertice; i++)
{
for (int j = 1; j <= vertice; j++)
{
cout << e[i][j] << " ";
}
cout << endl;
}
}
//Floyd_Warshall核心思想
void Floyd()
{
for (int k = 1; k <= vertice; k++)
{
for (int i = 1; i <= vertice; i++)
{
for (int j = 1; j <= vertice; j++)
{
//INT_MAX + INT_MAX 会溢出
if (e[i][k] < INT_MAX && e[k][j]<INT_MAX && e[i][j] > e[i][k] + e[k][j])
{
e[i][j] = e[i][k] + e[k][j];
}
}
}
}
}
};
int main()
{
Floyd_Warshall floy(4, 8);
floy.Init_Floyd();
floy.GetEdgeInfo();
cout << "初始信息：" << endl;
floy.Print();
floy.Floyd();
cout << "多源最短路径（）任意两个节点之间的最短路径：" << endl;
floy.Print();
return 0;
}
文章来源：https://www.toymoban.com/news/detail-416107.html
4.总结
可以借助Floyd_Warshall算法得到任意两点之间的最短路径。时间复杂度为O(N^3)。
值得注意的是，Floyd_Warshall算法可以处理带负权边的图，但不能处理带有“负权回路”的图。因为带有“负权回路”的图两个节点之间可能没有最短路径。例如，下面这个案例就不能使用该算法。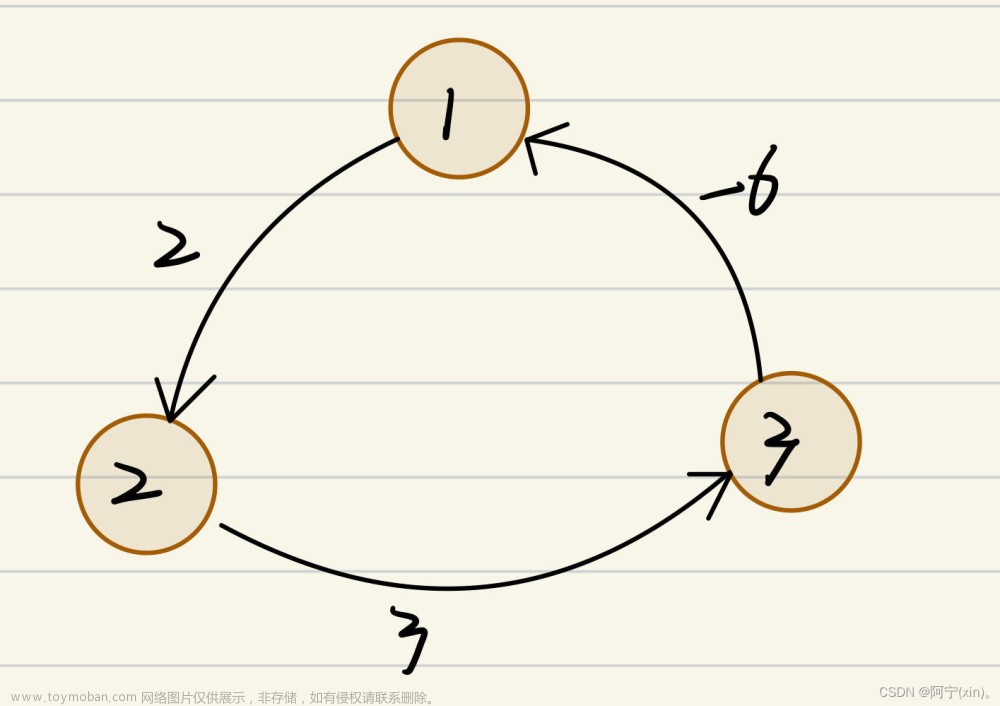
文章来源地址https://www.toymoban.com/news/detail-416107.html
到了这里，关于Floyd_Warshall算法详解及实现（多源最短路径）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
