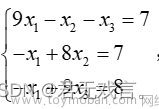非线性方程组——牛顿迭代求根-Toy模板网

这篇具有很好参考价值的文章主要介绍了非线性方程组——牛顿迭代求根。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

背景

三维曲面函数的参数方程 x(u,v)，y(u,v) ，z(u,v),且曲面满足凸性质，u属于[0，1]，v属于[0，1]，则在xoy平面任给一点p，过点p做一条平行与z轴的直线，假如该直线与曲面相交与一点，求该点的u，v值。用c++程序编写该数学案例，考虑继承和多态，要求用户给定的曲面作为输入，输出为u，v值。

1 案例分析

假设已知点p在曲面上的投影坐标为（ $x_0,y_0,t$ ）
$x_0 = x(u,v)\\ y_0 = y(u,v)$
故令
$F:\begin{cases} f = x(u,v) - x_0\\ g = y(u,v)-y_0 \end{cases}$
则该问题可以转换为求解关于 $f, g$ 方程组的解

2 算法实现步骤

由于用户指定函数不清楚为线性方程组还是非线性方程组，因此求解该方程组的根采取最优化方法中的牛顿迭代法求解。

由 $(u, v)$ 的范围，可设置其迭代初值 $u_0 = 0.5$ $v_0 = 0.5$ 精度 $esp = 10^{-6}$
牛顿迭代法公式（多元）： $\vec x_{k+1} = \vec x_{k} -J^{-1} \cdot \vec F$ ( $J^{-1}$ 为雅可比矩阵的逆矩阵， $\vec x_{k+1} = (u_{k+1},v_{k+1})^T$ , $\vec x_{k} = (u_{k},v_{k})^T$ )
将迭代初值带入依次迭代出 $\vec x_1,\vec x_2,\vec x_3，\cdots\cdots$
终止条件 $\lvert x_{k+1} - x_{k}\rvert$ < $esp = 10^{-6}$
将Newton-iteration 算法接口进行封装，生成DLL工程
用户自己指定曲面，隐式调用DLL工程，调用写的牛顿迭代接口，计算出曲面参数 $u, v$ 的值。

3 代码实现

3.1 牛顿迭代API封装

//用户函数基类
//User_Base.h
#pragma once
#include"dll_h.h"

class DLL_API User_Base
{
public:
	virtual double f(const double u, const double v) = 0;
	virtual double g(const double u, const double v) = 0;

};

//用户函数子类
//User_function.h
#pragma once
#include"dll_h.h"
#include"User_Base.h"

class DLL_API User_function:public User_Base
{
public:
	 double f(const double u, const double v);
	 double g(const double u, const double v);

};

//用户定义子类函数的实现
//User_function.cpp
#include"User_function.h"
#include<cmath>

double User_function::f(const double u, const double v)
{
	return pow(u, 3) + 3 * pow(v, 2) - 1;   //此处应该减x0，用1代替
}

double User_function::g(const double u, const double v)
{
	return pow(v, 3) + 3 * pow(u, 2) - 1;   //此处应该减y0，用1代替
}

//创建牛顿迭代类
//newton.h
#pragma once
#include"User_Base.h"
#include"User_function.h"
#include<iostream>
#include <iomanip>
#include"dll_h.h"
using namespace std;

class DLL_API newton
{
public:

	//构造函数
	newton(User_Base* m_user, double m_u0, double m_v0);


	//对f对u求导
	double fu(const double u, const double v);
	//对f对v求导
	double fv(const double u, const double v);
	//对g对u求导
	double gu(const double u, const double v);
	//对g对v求导
	double gv(const double u, const double v);

	//交换初值
	void swap(double& a, double& b);

	//牛顿迭代
	void newton_iteration();

	//析构函数
	~newton();


	double u0;
	double v0;
	User_Base* user;

};

//牛顿迭代实现
//newton.cpp
#define DLL
#include"newton.h"

constexpr double esp = 1e-6; //精度
constexpr auto N = 100;  //迭代最大次数 
constexpr double delta = 0.00001;  //求导delta值

//构造函数
newton::newton(User_Base* m_user, double m_u0, double m_v0)
{
	user = m_user;
	u0 = m_u0;
	v0 = m_v0;
}


//f对u导数
double newton::fu(const double u, const double v)
{
	double num = (user->f(u + delta, v) - user->f(u - delta, v)) / (2 * delta);
	return num;
}
//f对v的导数
double newton::fv(const double u, const double v)
{
	double num = (user->f(u, v + delta) - user->f(u, v - delta)) / (2 * delta);
	return num;
}
//g对u的导数
double newton::gu(const double u, const double v)
{
	double num = (user->g(u + delta, v) - user->g(u - delta, v)) / (2 * delta);
	return num;
}
//g对v的导数
double newton::gv(const double u, const double v)
{
	double num = (user->g(u, v + delta) - user->g(u, v - delta)) / (2 * delta);
	return num;
}

void newton::swap(double& a, double& b)
{
	double temp = a;
	a = b;
	b = temp;
}

void newton::newton_iteration()
{
	//user = new User_function();
	//d_user = new d_func();

	double u = 0, v = 0, det = 0;
	double n = 0;//统计迭代次数

	do
	{
		//v[0][0]-fu v[0][1]-fv v[1][0]-gu v[1][1]-gv
		//雅可比行列式
		double det 如果是这样写 那么就每次出这个循环之后det都会被置为0 直接写det 者和上面定义的det是同一个
		det =fu(u0, v0) * gv(u0, v0) - fv(u0, v0) * gu(u0, v0);

		//雅可比矩阵的逆
		double J[2][2] = { gv(u0, v0) / det,-fv(u0, v0) / det,-gu(u0, v0) / det,fu(u0, v0) / det };

		//若det == 0 ，无法计算雅可比矩阵的逆，退出循环
		if (abs(det) < esp) { break; };

		//迭代公式
		u = u0 - (J[0][0] * user->f(u0, v0) + J[0][1] * user->g(u0, v0));
		v = v0 - (J[1][0] * user->f(u0, v0) + J[1][1] * user->g(u0, v0));

		//记录每次迭代的迭代次数
		cout << "迭代次数:" << n++ << std::endl;
		if (n == N) //限定迭代次数，防止一直进行迭代
		{
			break;
		}
		else
		{
			std::cout.unsetf(std::ios::fixed);
			std::cout << std::setprecision(8) << "u = " << u << std::endl;
			std::cout << std::setprecision(8) << "v = " << v << std::endl;
			std::cout << "det:" << det << std::endl;

			//交换u,v值
			swap(u0, u);
			swap(v0, v);
		}

	} while (abs(u - u0) > esp && abs(v - v0) > esp);

	u = u0;
	v = v0;

	std::cout << "-------------------------" << std::endl;
	if (u >= 0 && u <= 1 && v >= 0 && v <= 1 && abs(det) < esp)
	{
		std::cout << "u = " << u << std::endl;
		std::cout << "v = " << v << std::endl;
	}
	else
	{
		std::cout << "没有找到对应的u，v值" << std::endl;
	}

}

newton::~newton()
{
	if (user != NULL)
	{
		delete user;
		user = NULL;
	}
}

//生成DLL时必须宏定义导出
//dll_h.h
#pragma once
//宏定义导出
#ifdef DLL//如果定义了DLL 就定义 DLL_API为 __declspec(dllexport)
#define DLL_API __declspec(dllexport)//导出
#else 
#define DLL_API __declspec(dllimport)//导入
#endif

//主函数函数调用
#include<iostream>
using namespace std;
#include"User_Base.h"
#include"newton.h"

int main()
{
	User_Base* user = new User_function();
	newton n(user,0.5, 0.5);
	n.newton_iteration();
	user = NULL;

	system("pause");
	return 0;
}

3.2 DLL库创建-隐式调用DLL库

将header文件和lib&&Dll文件放到你要调用的程序下面，在你的vs下面#include相关的头文件如下图所示。

非线性方程组——牛顿迭代求根

相关DLL创建和调用教程地址
DLL库创建与隐式调用教程
b站-编写动态，链接库
Visual Studio提示由于找不到dll，无法继续执行代码的问题解决

4 注意事项

配置解决平台X86/X64都可以(x64对应的是64位的操作系统x86对应的是win32的一个操作系统，我们编译的时候用的一般都是x86)，但是这个导出的DLL，用户引用的时候尽量和导出时的DLL平台一致
隐式调用动态库（DLL）时，需要三个文件分别为以.h .lib .dll为后缀名的文件，其中.h文件为你动态库中的头文件，.lib为符号文件，.dll为函数可执行代码文件。三者具体区别为【1】

非线性方程组——牛顿迭代求根

当我们调用我们dll库时，如果“找不到dll”的错误，可以将我们的.lib文件和.dll文件放到调用dll库文件（必须和.exe文件放到一起不然的话也会报错）的debug文件下（因为.exe文件一般都放在debug文件的下面）。
当我们有太多头文件中的函数需要___declspec(dllexport) 时候，我们可以创建一个类似与此案例中的dll_h.h，然后让每个头文件中都包含dll_h.h，直接对函数或者类进行宏定义。在定义宏定义的时候我们要注意是“导入”还是“导出”，判别方法我们可以将鼠标放到导入和导出的宏定义上面的提示进行判断。在此案例中需要导出的类就只有newton类，所以在定义宏时也只需要在其源文件中首行定义#define DLL就行

//生成DLL时必须宏定义导出
//dll_h.h
#pragma once
//宏定义导出
#ifdef DLL//如果定义了DLL 就定义 DLL_API为 __declspec(dllexport)
#define DLL_API __declspec(dllexport)//导出
#else
#define DLL_API __declspec(dllimport)//导入
#endif  ```

在本文这种没有提前定义宏的，还需要在源文件重新定义#define DLL，注意必须在源文件的第一行加入#define DLL，因为你用的是ifdef（if define ，如果定义了宏，注意与ifndef的区别）
#ifndef、__declspec(dllexport)、extern “C“的学习（写的非常好）
主函数中的user指向堆区的内存在dll工程中的析构函数中进行了释放，在主函数中不要对其进行释放，否则重复释放了堆区内存。
1. “C++ 全局变量被自身文件/项目内其他文件/动态链接库(DLL)之外文件使用 ” 一定要特别注意！！！！

5 API说明

接口形式
//初始化
Newton n (1, 2, 3);
1- 用户所创建指向子类的父类指针
2，3 - 牛顿迭代初值

//调用牛顿迭代API
n.newton_iteration();

思考

利用多态创建函数。由于基类指针指向子类对象不同，最后得出得结果也会不同，这个结果会覆盖我们所写的dll工程中的结果，所有当我们输入的函数不同的时，最后得出的结果也不回相同。如何不利用多态来创建函数，则我们在封装dll时，dll工程中的函数就是固定死的，不管我们如何在我们的exe程序中修改这个函数，最后得出得结果都不会发生变化。
用牛顿迭代法求解方程组的解的时候，遇到方程组有多个解的时候牛顿法就求解不了，牛顿法只能求解到这个方程组的解离迭代点最近的那个解。对于我这个例子想要用牛顿迭代法求解的话，我们还需要大致判断有几个解，这个数学案例中给了u，v的初始范围为[0,1]，大致判断f，g函数的单调性，大致画出f，g函数的函数图像，如果f，g函数有几个交点就对应有几个根。
一个类的成员函数作为地址进行回调处理的时候，**其实还传入了一个this指针，所有在我们接受这个这个成员函数的地址的时候，我们还需要用引用或者指针的方式来指定是那个对象的this指针。**对于这种回调函数的写法，最好采用函数包装器function来写。

#include <iostream>
#include <functional>//function需要包含头文件
using namespace std;
constexpr auto delta = 0.000000000001;


class User_function
{
public:
	double f(const double x, const double y)
	{
		return x * x * x + 3 * y * y - 3;
	}
};

//fx函数求导;;
class DerivativeX
{
public:

	//初始化构造函数
	//DerivativeX(function< double(User_function*, const double x, const double y)> m_F, User_function user, const double x, const double y)
	DerivativeX(function< double(User_function&, const double x, const double y)> m_F, User_function user, const double x, const double y)
	{
		F = m_F;
		d_user = user;
		//d_user = &user;//指针指向类对象User_function user的地址
		X = x;
		Y = y;
	}

	//F对X求导
	double func()
	{
		double num = (F(d_user, X + delta, Y) - F(d_user, X - delta, Y)) / (2 * delta);
		return num;
	}

	double X;
	double Y;
	User_function d_user;
	//User_function* d_user;
	function< double(User_function&, const double x, const double y)> F;
};

int main()
{
	User_function user;
	//隐藏的this指针用User_function&接收 或者user_function*  
	//function< double(User_function*, const double x, const double y)> m_F = &User_function::f;
	function< double(User_function&, const double x, const double y)> m_F = &User_function::f;
	DerivativeX fu(m_F, user, 0.5, 0.5);
	//m_F-回调函数 user，0.5，0.5 - 回调函数的参数
	fu.func();
	cout << "函数在x = 0.5，y = 0.5的导数为：" << fu.func() << endl;
	system("pause");
	return 0;
}

疑问

为什么我牛顿迭代里面的关于求导的函数对象已经写死了，按理来说调用DLL工程的时候。用户创建函数时，调用这个DLL工程时候，函数的名称也只能为f，g，要是改成其他的了（如：h，j）程序应该运行不了。但是用户自己定义这个函数的时候，这个函数的对象是可以顺便修改的，修改之后得出来的u，v值也还是正确的。希望以后对知识理解更加深刻了之后能够发现其中的问题。

如下面案例，生成DLL工程时，牛顿迭代里面关于求导的函数已经写死，调用的函数对象都是f,g，封装之后用户写函数调用的时候应该也只能写f,g呀！

//f对u导数
double newton::fu(const double u, const double v)
{
	double num = (user->f(u + delta, v) - user->f(u - delta, v)) / (2 * delta);
	return num;
}
//f对v的导数
double newton::fv(const double u, const double v)
{
	double num = (user->f(u, v + delta) - user->f(u, v - delta)) / (2 * delta);
	return num;
}
//g对u的导数
double newton::gu(const double u, const double v)
{
	double num = (user->g(u + delta, v) - user->g(u - delta, v)) / (2 * delta);
	return num;
}
//g对v的导数
double newton::gv(const double u, const double v)
{
	double num = (user->g(u, v + delta) - user->g(u, v - delta)) / (2 * delta);
	return num;
}

但是用户自己定义这个函数的时候，这个函数的对象是可以顺便修改的(函数对象改为了i，g)，修改之后得出来的u，v值也还是正确的。

//User_Base.h
#pragma once
class User_Base
{
public:
	virtual double i(const double u, const double v) = 0;
	virtual double g(const double u, const double v) = 0;
};

//User_function.h
#pragma once
#include"User_Base.h"
class User_function :public User_Base
{
public:
	double i(const double u, const double v);
	double g(const double u, const double v);
};

//User_function.cpp
#include"User_function.h"
#include<cmath>

double User_function::i(const double u, const double v)
{
	return pow(u, 4) + 3 * pow(v, 3) - 2;
}
double User_function::g(const double u, const double v)
{
	return pow(v, 4) + 3 * pow(u, 3) - 3;
}

//main().cpp
#include<iostream>
using namespace std;
#include"User_Base.h"
#include"header/newton.h"


int main()
{
	User_Base* user = new User_function;

	newton n(user, 0.5, 0.5);
	n.newton_iteration();

	user = NULL;
	system("pause");
	return 0;
}