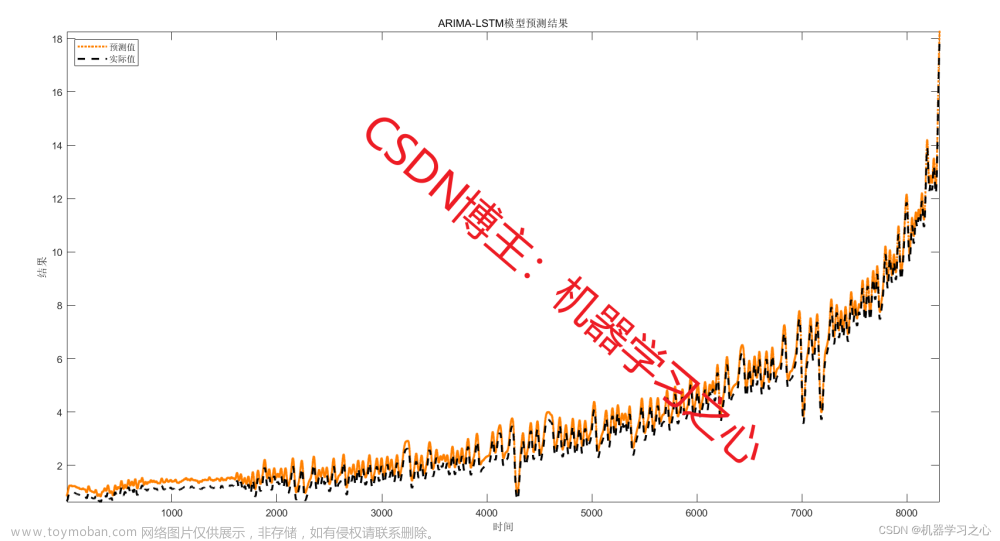
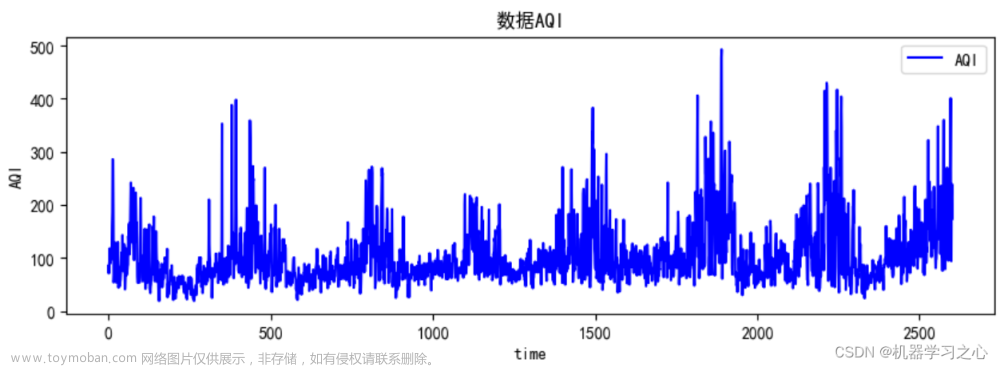
时间序列是按时间顺序排列的、随时间变化且相互关联的数据序列。分析时间序 列的方法构成数据分析的一个重要领域,即时间序列分析。
如果在预测时间范围以内,无突然变动且随机变动的方差较小,并且有理由认为过去和现在的演变趋势将继续发展到未来时,可用一些经验方法进行预测。
一、移动平均法
移动平均法有简单移动平均法,加权移动平均法,趋势移动平均法等。
1.1简单移动平均
设观测序列为,取移动的项数N<T,当预测目标的基本趋势是在某一水平上下波动时,可用一次简单移动平均方法建立预测模型:

实质是用最近 N 期序列值的平均值作为未来各期的预测结果。
其标准误差为

一般 N 取值范围: 5 ≤ N ≤ 200 。当历史序列的基本趋势变化不大且序列中随机变动成分较多时, N的取值应较大一些。否则 N 的取值应小一些。在有确定的季节变动周期的资料中,移动平均的项数应取周期长度。选择最佳 N 值的一个有效方法是,比较若干模型的预测误差。预测标准误差最小者为好
例题1 某企业 1 月~11 月份的销售收入时间序列如表 1 示。试用一次简单滑动平均法预测第 12 月份的销售收入。

解析
N=4时,预测公式为

预测值,预测的标准误差为

N=5时,预测公式为

预测值,预测的标准误差为

N = 4 时,预测的标准误差较小,所以选取 N = 4 。预测第12月份的 销售收入为 993.6。
Matlab实现如下
clc,clear
y=[533.8 574.6 606.9 649.8 705.1 772.0 816.4 892.7 963.9 1015.1
1102.7];
m=length(y);
n=[4,5]; %n 为移动平均的项数
for i=1:length(n)
%由于 n 的取值不同,yhat 的长度不一致,下面使用了细胞数组
for j=1:m-n(i)+1
yhat{i}(j)=sum(y(j:j+n(i)-1))/n(i);
end
y12(i)=yhat{i}(end);
s(i)=sqrt(mean((y(n(i)+1:m)-yhat{i}(1:end-1)).^2));
end
y12,s注:简单移动平均法只适合做近期预测,而且是预测目标的发展趋势变化不大的情况。 如果目标的发展趋势存在其它的变化,采用简单移动平均法就会产生较大的预测偏差和滞后。
1.2 加权移动平均
在简单移动平均中,所选的近期数据在预测计算中所占比重是相同的,但是近期数据一般包含着关于未来的信息,因此给予更高的权重。类似于加权平均数。
设时间序列为,加权移动平均公式为

为t 期加权移动平均数;为 的权数,它体现了相应的 在加权平均数中的重要性。
利用加权移动平均数来做预测,其预测公式为

即以第t 期加权移动平均数作为第t +1期的预测值。
例题2 我国 1979~1988 年原煤产量如表 2 所示,试用加权移动平均法预测 1989 年 的产量


解 取,按预测公式

计算三年加权移动平均预测值,其结果列于表 2 中。1989 年我国原煤产量的预测 值为(亿吨)

该预测值明显偏低,所以我们用平均相对误差进行修正,其方法是:先计算各年预测值与实际值的相对误差,例如 1982 年为

Matlab实现如下
y=[6.35 6.20 6.22 6.66 7.15 7.89 8.72 8.94 9.28
9.8];
w=[1/6;2/6;3/6];
m=length(y);n=3;
for i=1:m-n+1
yhat(i)=y(i:i+n-1)*w;
end
yhat
err=abs(y(n+1:m)-yhat(1:end-1))./y(n+1:m)
T_err=1-sum(yhat(1:end-1))/sum(y(n+1:m))
y1989=yhat(end)/(1-T_err)注:在加权移动平均法中, 的选择,同样具有一定的经验性。一般的原则是:近期数据的权数大,远期数据的权数小。至于大到什么程度和小到什么程度,则需要按照预 测者对序列的了解和分析来确定
1.3趋势移动平均
简单移动平均法和加权移动平均法,在时间序列没有明显的趋势变动时,能够准确 反映实际情况。但当时间序列出现直线增加或减少的变动趋势时,用简单移动平均法和 加权移动平均法来预测就会出现滞后偏差。因此,需要进行修正,修正的方法是作二次移动平均,利用移动平均滞后偏差的规律来建立直线趋势的预测模型。这就是趋势移动平均法。
一次移动的平均数为

在一次移动平均的基础上再进行一次移动平均就是二次移动平均,其计算公式为

设时间序列 从某时期开始具有直线趋势,且认为未来时期也按此直线趋势变 化,则可设此直线趋势预测模型为

其中t 为当前时期数;m 为由t 至预测期的时期数;为截距;为斜率。两者又称为平滑系数。
根据移动平均值来确定平滑系数

例题3 我国1965~1985 年的发电总量如表 3 所示,试预测 1986 年和 1987 年的发电总量。

解 先做出原数据的散点图图1

由散点图 1 可以看出,发电总量基本呈直线上升趋势,可用趋势移动平均法来预测。
取 N = 6 ,分别计算一次和二次移动平均值并列于表 3 中。

再由公式得

于是,得t = 21时直线趋势预测模型为

预测 1986 年和1987 年的发电总量为


Matlab实现文章来源:https://www.toymoban.com/news/detail-417465.html
clc,clear
load y.txt %把原始数据保存在纯文本文件 y.txt 中
m1=length(y);
n=6; %n 为移动平均的项数
for i=1:m1-n+1
yhat1(i)=sum(y(i:i+n-1))/n;
end
yhat1
m2=length(yhat1);
for i=1:m2-n+1
yhat2(i)=sum(yhat1(i:i+n-1))/n;
end
yhat2
plot(1:21,y,'*')
a21=2*yhat1(end)-yhat2(end)
b21=2*(yhat1(end)-yhat2(end))/(n-1)
y1986=a21+b21
y1987=a21+2*b21 文章来源地址https://www.toymoban.com/news/detail-417465.html
到了这里,关于时间序列分析--移动平均法预测模型的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!