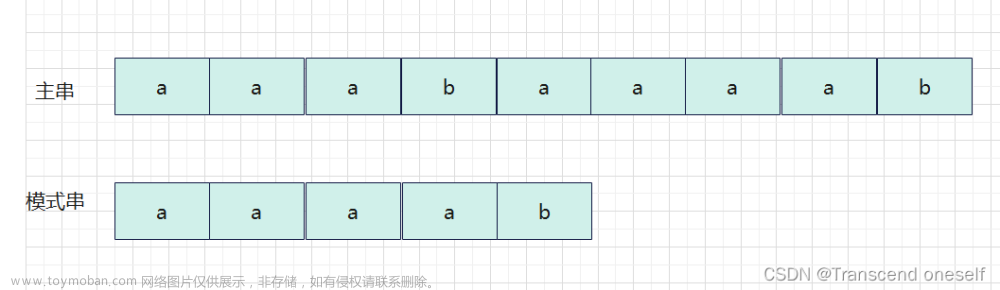
KMP算法——（手把手算next数组）-Toy模板网

这篇具有很好参考价值的文章主要介绍了KMP算法——（手把手算next数组）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

KMP算法

该算法核心是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数，从而达到快速匹配的目的。
KMP算法与BF算法（暴力算法）区别在于，主串的i不会回退，并且模式串的j不会每次都回到0位置。

第一个问题：为什么主串的i不需要回退？

看如下两个字符串：
a b c d a b g h
a b g
假设此时 i 指向 c，j 指向 g，匹配失败。
就算 i 退回到 b 的位置，此时和模式串的 0 位置 a 也不一样。

第二个问题：模式串的j回退的位置？

看如下两个字符串：
a b c a b g h a b c a b c
a b c a b c
假设此时 i 指向 g，j 指向 c，匹配失败。
此时 i 不进行回退，因为在这个地方前，两个字符串是有一部分相同的。
因此，我们观察，当我们保持 i 不动， j 退回到第三个位置也就是 c 时，不难发现两个字符串前 a b 是一样的。
因此，我们需要借助 next 数组，帮助我们找到 j 需要回退的位置。

next数组

KMP算法的精髓就是next数组，next[j]=k，表示不同的 j 对应一个 k 值；k 表示模式串下标为 j 的元素，匹配失败时，要退回的位置。
求k值的规则：

在模式串中，以下标为 0 开始，以下标为 j-1 结束分别找到两个相同的字符串
得到的字符串长度就是 k 值

不管什么数据 next[0]=-1; next[1]=0;

例如求模式串 a b c a b c a b 的next数组(数组下标从0开始)

首先next[0]=-1 next[1]=0

对于数组下标为 j=2 的 c ，寻找以 a 开头，以 b 结尾的两个相同字符串，找不到，则字符串长度为 0，即 k=0 —— next[2]=0

对于数组下标为 j=3 的 a ，寻找以 a 开头，以 c 结尾的两个相同字符串，找不到，则字符串长度为 0，即 k=0 —— next[3]=0

对于数组下标为 j=4 的 b ，寻找以 a 开头，以 a 结尾的两个相同字符串，找到 a 字符串，则字符串长度为 1，即 k=1 —— next[4]=1

对于数组下标为 j=5 的 c ，寻找以 a 开头，以 b 结尾的两个相同字符串，找到 ab 字符串，则字符串长度为 2，即 k=2 —— next[5]=2

对于数组下标为 j=6 的 a ，寻找以 a 开头，以 c 结尾的两个相同字符串，找到 abc 字符串，则字符串长度为 3，即 k=3 —— next[6]=3

对于数组下标为 j=7 的 b ，寻找以 a 开头，以 a 结尾的两个相同字符串，找到 abca 字符串，则字符串长度为 4，即 k=4 —— next[7]=4

因此该字符串的next数组为 -1 0 0 0 1 2 3 4

在上面next数组计算时，不难发现，我们可以通过前一项的k，计算当前项的k，有两种情况：

情况一：arr[k] == arr[j-1]
例如我们在计算数组a b c a b c a b 中下标为 j=6 的 a 的 k 值时。
此时 j-1=5 的 k=2 指向下标为2的 c，说明存在相同字符串 ab 即 arr[0]…arr[k-1=1] == arr[(j-1)-k=3]…arr[(j-1)-1=4]。又此时 arr[k=2] == arr[j-1=5] (== c)，那么连接起来便存在相同字符串 abc，即 arr[0]…arr[k=2] == arr[(j-1)-k=3]…arr[j-1=5] 因此在上一项的基础上增加一项（从 ab 到 abc），即 next[j] = k+1 = 2+1 = 3

情况二：arr[k] != arr[j-1]
例如我们在计算数组 a b c a b e a b 中下标为 j=6 的 a 的 k 值时。
此时 j-1=5 的 k=2 指向 c，说明存在相同字符串 ab 即 arr[0]…arr[k-1=1] == arr[(j-1)-k=3]…arr[(j-1)-1=4]。又此时 arr[k=2] != arr[j-1=5] ，那么借助 k 下标的 next 值继续回退，回退到了 0 下标，此时 arr[k=0] != arr[j-1=5] 仍然不相等，继续回退 k=-1 ，当 k=-1 数组越界，也就意味着不存在相匹配的字符串，因此 next[j] = k+1 = 0。

总结，如果是情况一或者k=-1数组越界，则 next[j] = k+1。否则为情况二，则 k=next[k] 一直回退，直到出现情况一或者k=-1数组越界。

C代码如下：

void GetNext(char* sub, int* next, int lenSub) {
	next[0] = -1;
	next[1] = 0;
	int j = 2;	// 当前下标
	int k = 0;	// 前一项的k，即前一项回退的下标
	// 此时 j=2 的前一项next数组值为0
	while(j < lenSub) {
		if (k == -1 || sub[j - 1] == sub[k]) {	// 情况一和数组越界情况：next[j] = k+1
			next[j] = k+1;	
			j++;	// 求下一个位置
			k++;
		}
		else {
			k = next[k];	// 情况二：不相等则回退
		}
	}
}

KMP主体

我们得到 next数组 后，便可开始从基础的暴力算法，升级为KMP算法。
借助 next数组，完成主串的i不会回退，模式串 的j回退到 next数组 中存放的相应位置。
str 表示主串，sub 表示模式串， pos 表示开始比较的位置。
C代码如下：文章来源地址https://www.toymoban.com/news/detail-417667.html

int KMP(char* str, char* sub, int pos) {
	assert(str && sub);
	int lenStr = strlen(str);
	int lenSub = strlen(sub);
	if (lenStr == 0 || lenSub == 0) {
		return -1;
	}
	if (pos < 0 || pos >= lenStr) {
		return -1;
	}

	// 对模式串sub创建next数组
	int* next = (int*)malloc(sizeof(int) * lenSub);
	assert(next);
	GetNext(sub, next, lenSub);

	// 进行遍历比较
	int i = pos;	// 遍历主串
	int j = 0;	// 遍历子串
	while (i < lenStr && j < lenSub) {
		if (j == -1 || str[i] == sub[j]) {	// j == -1 时，回退越界，一样进行++处理
			i++; j++;
		}
		else {
			j = next[j];	// 根据next数组进行回退
		}
	}

	// 模式串匹配主串，则会在模式串末尾结束
	if (j >= lenSub) {
		return i-j;
	}

	// 模式串不匹配主串
	return -1;
}